于罡，宋海洲

（华侨大学数学科学学院，福建 泉州 362021）

正则图的均匀边染色

于罡，宋海洲

（华侨大学数学科学学院，福建 泉州 362021）

研究正则图的均匀边染色，指出并非所有正则图都存在任意种颜色的均匀边染色.证明当l能够分解为整数k与偶数b的乘积时，l-正则图存在均匀k-边染色.同时，给出正则图均匀边染色的最小颜色数.

正则图；边染色；均匀边；几乎均匀边

图的染色问题是图论研究的经典领域.这是由于它在组合分析和实际生活中的广泛需要，如时间表问题、贮藏问题、电信通讯站点的频率分配问题、计算机网络结构设计区分问题，以及计算机和银行安全密码问题等.其中的一些网络及优化问题，可以进一步转化为均匀点染色、均匀边染色、均匀全染色等问题.图的染色的基本问题就是确定各种染色法的色数，而确定图的有关色数是一个十分困难的问题.文［1］证明对于任意v∈V（G），若k不能整除d（v），则图G存在均匀k-边染色.文［2］证明了所有的二分图都是可均匀染色的.文［3］证明了任意一个不为奇圈的连通外平面图都是均匀可染的.文［4］给出了Halin图的一些均匀边染色结果.文［5］研究了混合超图的星染色的若干性质.本文讨论正则图的均匀边染色，考虑的图都是有限无向简单图.

1 定义及引理

图G的点集和边集分别用V（G）和E（G）表示.对任意的v∈V（G），令dG（v）表示v的度，在不致引起混淆的情况下，简记为d（v）.如果对每个v∈V（G），均有dG（v）=l，无向图G称为l-正则的.图G的边染色是给图G的每条边分配一种颜色，用正整数1，2，…表示颜色，若C是边集E到集合｛1，2，…，k｝的映射，即C∶E→｛1，2，…，k｝，则称C为图G的k-边染色［6］.令iC（v）表示在染色C中与G的顶点v关联的i色边的数目.在不致引起混淆的情况下，简记i（v）=iC（v）.

定义1 假设C为图G的k-边染色，对于任意的v∈V（G）和任意的i，j∈｛1，2，…，k｝，如果|i（v）-j（v）|≤1，则称C为图G的均匀边染色.如果|i（v）-j（v）|≤2，则称C为图G的几乎均匀边染色.

令E（i）表示图G的边染色C中i色边组成的集合，E（i）∪E（j）的边导出子图记为G（i，j）.对任意的v∈V（G），令G（v.，i，j）表示G（i，j）中含顶点v的连通分支.

下面给出4个重要引理.

引理2［1］设图G为简单图，k≥2.如果对任意v∈V（G），有d（v）≢0（modk），则图G存在k种颜色的均匀边染色.

引理3［8］设图G为连通图，则图G一定存在2-边染色C，其满足以下3个条件：（1）若图G为欧拉图且|E|为奇数，则对V中任意选取的顶点u，有|1（u）-2（u）|=2.对于所有的v∈V（G）｛u｝，均有1（v）-2（v）=0.（2）若图G为欧拉图且|E|为偶数，则对于所有的v∈V（G），有1（v）-2（v）=0.（3）若图G不是欧拉图，则对所有的v∈V（G），有|1（v）-2（v）|≤1.

引理4［7］设k为大于1的任意整数，则存在图G的k-边染色C，使得对任意v∈V（G），i，j∈｛1，2，…，k｝，有|i（v）-j（v）|≤2.

设k≥1，C为图G的几乎均匀k-边染色.对任意的v∈V（G），令

显然，对图G的均匀边染色有σ（C）=0.

若图G中的链K=（v0，e1，v1，e2，…，vr-1，er，vr）满足如下的条件，则称K为图G由v0发出的一条（α，β）-交换链.

（i）对任意的1≤i≤r，顶点vi-1和vi是边ei的两个不同端点；

（ii）K中所有的边互异，且交替染以α色和β色；

（iii）e1染α色，且α（v0）＞β（v0）.

类似地，令γ记边er的颜色，γ¯记｛α，β｝中的另一种颜色，则γ（vr）＞γ¯（vr）.

若图G由v0发出的一条（α，β）-交换链以一条β色边到达v0，则再从一条与v0关联的还没有在交换链上出现的α色边开始，继续找下去.这条（α，β）-交换链的终点vr可能与始点v0相同.

令K为一条由顶点发出的（α，β）-交换链，若不存在另一条由顶点发出的（α，β）-交换链K′⊂K，则称K为由顶点x发出的极小（α，β）-交换链.

若α（v0）≥β（v0）+2，则通过交换K上的两种颜色可能使染色更均匀；然而，若α（v0）=β（v0）+2且v0=vr，通过交换K上的两种颜色并不能改善其染色.可以看出，交换交换链上的两种颜色并不会使染色更坏.

2 主要结论

由引理2可知，当l≢0（modk）时，l-正则图存在k种颜色的均匀边染色.

下面讨论一种l≡0（modk）的情形.

定理1 设l=bk，b为不小于2的偶数，则l-正则图G存在k种颜色的均匀边染色.

证明 由引理4可知，图G存在k种颜色的几乎均匀边染色，在图G的所有k种颜色的几乎均匀边染色中，令C为使σ（C）达到最小的染色.如果σ（C）=0，则C为均匀k-边染色.

下面用反证法，假设σ（C）＞0，则存在x∈V（G）和α0，β∈｛1，2，…，k｝，使得α0（x）=β（x）+2.

考虑边导出子图G（x.，α0，β）.如果H（x.α0，β）是有奇数条边的欧拉图，满足α0（x）=β（x）+2，并且对每个v∈V（H）｛x｝，均有α（v）=β（v）成立，则称H为图G在顶点x处的障碍子图.

如果对某个x∈V（G），α0（x）=β（x）+2，但H=G（x.α0，β）不是障碍子图，由引理3，可用颜色α0，β对H的边重新染色，从而得到图G的一个几乎均匀边染色C′，满足σ（C′）＜σ（C），产生矛盾.

下设H=G（x.α0，β）为一个障碍子图.另设y0为与x通过α0色边关联的一点，记边（x，y0）=e0.

因为C为几乎均匀边染色，易知对任意v∈V（G），i∈｛1，2，…，k｝，必有i（v）∈｛b-1，b，b+1｝.若存在i∈｛1，2，…，k｝，使得i（v）=b-1，则必存在j∈｛1，2，…，k｝，使得j（v）=b+1成立，反之亦然.这样，障碍子图H=G（x.α0，β）中，必有α0（x）=b+1，β（x）=b-1.

情形1 α0（y0）=β（y0）=b+1，则存在α1∈｛1，2，…，k｝使得α1（y0）=b-1.

首先将边e0重新染以β色.在图G的当前染色中，α0（x）=β（x）=b，且β（y0）=b+2，α0（y0）=b.记由y0发出的（β，α1）极小交换链为K.如果K不终止于y0，则交换K中边的颜色后，β（y0）=b+1，α1（y0）=α0（y0）=b；如果K终止于y0本身，则交换K中边的颜色后，β（y0）=α0（y0）=b，α1（y0）=b+1.这样一来，每种情况都得到了图G的仍为几乎均匀边染色的染色C′，且σ（C′）＜σ（C）.

情形2 α0（y0）=β（y0）=b-1.存在α1∈｛1，2，…，k｝，使得α1（y0）=b+1.将边e0重新染以β色.在图G的当前染色中，α0（x）=β（x）=b，且β（y0）=b，α0（y0）=b-2.记由y0发出的（α1，α0）极小交换链为K.如果K不终止于y0，交换K中边的颜色后，α1（y0）=b，α0（y0）=b-1，β（y0）=b，图G得到改进，产生矛盾.如果K终止于y0本身，交换K中边的颜色后，α1（y0）=b-1，α0（y0）=b，β（y0）=b，图G同样得到改进，产生矛盾.

情形3 α0（y0）=β（y0）=b，顶点x通过α0色边相关联的任意点，均有α0（v）=β（v）=b.不然，由情形1，2可知，对染色改进，产生矛盾.

显然，由x点发出的（α0，β）极小交换链K必以一条α0色边终止于x本身；否则，交换K中边的颜色，在新染色中，α（x）=β（x）=b，C得到改进，产生矛盾.

x点通过β色边关联的任意点v，必有α0（v）=β（v）=b.不然，α0（v）=β（v）=b+1或α0（v）=β（v）=b-1，则可以交换K中边的颜色，在新染色中α（x）=b-1=β（x）-2.此时，障碍子图为G（x.，β，α0）.

由情形1，2的讨论可知，对图G的当前染色改进，产生矛盾.这样，得出H=G（x.，α0，β）中与x关联的任意点，均有α0（v）=β（v）=b.将e0重新染以β色，在图G的当前染色中，有

α0（x）=β（x）=b，

β（y0）=b+1=α0（y0）+2.

在此情形下，图H中任意点的度均为2b.假设图H的阶为q，因为b是偶数，则由引理1可知，|E（H）|=2b·q/2=b·q为偶数，与障碍子图的定义矛盾.证毕.

实际上，当l=bk，b为奇数时，l-正则图未必是可以均匀k-边染色的.例如，b=1，k=4时的完全图K5，就不存在4种颜色的均匀边染色；而b=3，k=2的奇数阶l-正则图，也不存在2种颜色的均匀边染色.

由文［2］知，当正则图可以2部划分时，其存在任意种颜色的均匀边染色.

综上所述，得到如下的推论.

推论1 并非所有正则图都存在任意种颜色的均匀边染色.

由引理2可知，任意简单图G都存在Δ（G）+1种颜色的均匀边染色，其中

Δ（G）=max｛dG（x）∶x∈V（G）｝.

对于给定的简单图G，定义

χ″（G）=min｛k∶G存在k（k＞1）种颜色的均匀边染色｝，

显然，χ″（G）是有意义的.

定理2 设图G为连通的m阶l-正则图，则

（i）χ″（G）=3，当l=2（2s+1），其中s为非负整数，且m为奇数；

（ii）χ″（G）=2，其他情况.

证明 （1）若l为奇数，由引理2可知，χ″（G）=2；

（2）若l≡0（mod 4），由引理1可知，|E（G）|=ml/2为偶数，再由引理3可得，χ″（G）=2；

（3）若l≢0（mod 4），但l≡0（mod 2）且m为偶数，则|E（G）|亦为偶数，由引理3可知，χ″（G）=2.至此，证得定理2的（ii）情形.

下面讨论定理2的（i）情形.此时，图G为欧拉的且有奇数条边.

首先，证明χ″（G）≠2.在图G的任意2k-边染色C中，由|E（G）|为奇数，可知E（1）≠E（2），所以至少存在一点，不妨设为v0，使得1（v0）≠2（v0）.图G是欧拉图，可知d（v0）是偶数.又因为d（v0）=1（v0）+2（v0），所以必有|1（v0）-2（v0）|≥2，即C不是均匀边染色.由C的任意性，可知图G不存在2种颜色的均匀边染色，即χ″（G）≠2.

其次，证明χ″（G）=3.若l≢0（mod 3），则由引理2可知，图G存在3种颜色的均匀边染色，即有χ″（G）=3.若l≡0（mod 3），则l可以表示成l=6（2t+1）的形式，其中t为非负整数.

由引理4可知，图G存在一个几乎均匀3-边染色.在图G的所有几乎均匀3-边染色中，令C为使σ（C）达到最小的染色.如果σ（C）=0，则C为均匀3-边染色.

下面用反证法，假设σ（C）＞0，则存在v∈V（G）和α，β∈｛1，2，3｝，使得α（x）-β（x）=2.

如果边导出子图H=G（x.，α0，β）不是障碍子图，则由引理3可知，用颜色α，β对图H中的边重新染色，得到满足σ（C′）＜σ（C）的几乎均匀边染色C′，产生矛盾.

假设H=G（x.，α0，β）为障碍子图.对于任意的y∈V（H）｛x｝，因为C是几乎均匀边染色，所以必有

α（y）=β（y）=2（2t+1），

α（x）=2（2t+1）+1，β（y）=2（2t+1）-1.

且

设图H的阶为q，则由引理1可知

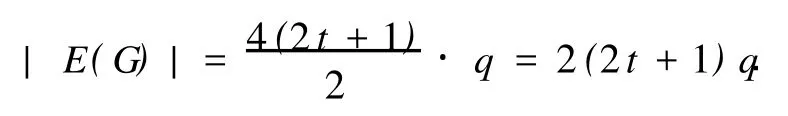
|E（G）|为偶数，与障碍子图的定义矛盾.从而定理2的情形（i）得证.证毕.

［1］HIL TON A J W，de WERRA D.A sufficient condition for equitable edge-coloring of simple graphs［J］.Discrete Mathematics，1994，128（1/3）：179-201.

［2］de WERRA D.Equitable colorations of graphs［J］.Reveu Francaise d’Informatique et de Recherche Operationelle，1971，5（3）：3-8.

［3］WU Jian-liang.The equitable edge-colouring of outerplanar graphs［J］.The Journal of Combinatorial Mathematics and Combinatorial Computing，2001，36（1）：247-253.

［4］宋慧敏，龙和平，吴建良.Halin图的均匀边染色［J］.山东大学学报：理学版，2003，38（2）：32-34.

［5］王志雄.混合超图的星染色［J］.华侨大学学报：自然科学版，1996，17（2）：123-126.

［6］宋慧敏，刘桂真.图的f-边覆盖染色［J］.数学学报，2005，48（5）：919-928.

［7］徐俊明.图论及其应用［M］.2版.合肥：中国科学技术大学出版社，2004：13.

［8］HAKIMI S L，KARIV O.A generalization of edge-coloring in graphs［J］.Journal of Graph Theory，1986，10（2）：139-154.

Equitable Edge-Coloring of Regular Graph

YU Gang，SON G Hai-zhou
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

The equitable edge-coloring of a regular graph is studied in this paper.It is shown that equitable edge-colorings with any colors can’t be done for all regular graphs.It is proved that al-regular graph has an equitable edge-coloring withkcolors whenl=kb，wherekandbare integer andbis even.Theminimum number of colors for a regular graph to have an equitable edge-coloring is given，too.

regular graph；edge coloring；equitable edge；nearly equitable edge

O 157.5

A

1000-5013（2010）06-0711-04

（责任编辑：陈志贤 英文审校：张金顺，黄心中）

2008-12-12

宋海洲（1971-），男，副教授，主要从事运筹与控制的研究.E-mail：hzsong@hqu.edu.cn.

福建省自然科学基金资助项目（Z0511028）