许小健,干 洪,张金轮

(1.芜湖市勘察测绘设计研究院,安徽 芜湖 241000;2.安徽工程科技学院,安徽 芜湖 241000)

随着软土地区铁路和高速公路的大力发展,软土路基的沉降问题日益突出[1]。有关路基沉降的研究已有相当多的报道,其中沉降预测问题一直是众多研究者广泛关注的问题。现有的沉降预测方法主要有两大类:一是根据固结理论基于土的本构模型,应用数值方法计算沉降量;二是根据实测资料推算沉降量与时间关系的预测方法。由于路基沉降影响因素的复杂性及本构模型参数选取困难等问题,基于固结理论的沉降计算值往往与实测值差异较大。因此,如何从前期的沉降数据来推算软土路基后期的沉降规律,这方面的研究工作具有重要意义。在第2类方法中,长期以来,常用的方法有双曲线法[2]、修正双曲线法[3]、指数曲线法[2]、Asaoka法[4]、灰色预测法[4]、星野法[5]等。

近来,有关研究结果表明,线性加载过程中,软土路基的沉降可以分为4个阶段[6]:沉降量线性增长阶段—沉降速率不断增加阶段—沉降速率递减阶段—沉降趋于稳定阶段,即软土路基沉降发展过程呈S形曲线。Logistic曲线的形状也呈S形,与沉降曲线特点极为一致,因此被用来描述沉降的发生发展过程,从而在沉降的预测中得到了应用[7]。除此之外,具有饱和增长趋势的S形曲线如Gompertz曲线模型[8]、Weibull曲线模型[9]、Usher曲线模型[10]等几种经验曲线模型也逐渐得到应用,取得了良好的效果。然而上述几种S形曲线模型在模型结构上仍然存在一些不足。针对这一缺点,笔者将用于资源预测的广义Usher模型[11]引入沉降预测中,通过对广义Usher模型的分析,表明了 Logistic模型、Bertalanffy模型、Gompertz曲线模型[8]、Weibull曲线模型[9]、Usher曲线模型[10]均为广义Usher模型的几种特例,因此,广义Usher模型具有更强的适应性;同时,鉴于合理的优化方法可以进一步改善模型的预测精度,本文选用笔者研发的基于并行优进策略的差分进化算法[12](DEPES算法)来优化模型结构参数。实例计算结果显示,本文给出的模型及参数优化方法有效,可取得满意的结果。

1 软土路基沉降预测的广义Usher模型

用于资源预测的广义Usher模型是以Usher模型为基础拓展建立起的一个新的生长曲线模型。其建立的微分表达式为[11]

式中:t为时间变量;α为时间t的修正因子;y为被描述事物的特征指标;r为增长速度因子,正实数;β为形状因子;L为y的上限。

对式(1)进行分离变量求解,得通解为

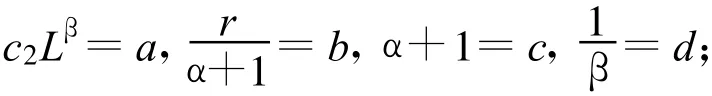
式中:s为沉降量;s∞为极限沉降量。

分析可知,在式(3)中,若令 c=1,a=d=-1,该模型可简化为指数曲线沉降预测模型;令c=1,该模型可简化为Usher沉降预测模型;若令a=-1,c=1,d=-3,该模型可简化为Bertalanffy沉降预测模型;若令c=d=1,该模型可简化为Logistic沉降预测模型;若令 a=d=-1,该模型可简化为Weibull沉降预测模型;若令微分表达式(1)中α=0,β→1,由式(1)经罗必塔法则求导后可得Gompertz模型的微分表达式,从而可以得到Gompertz沉降预测模型。由此可见,沉降预测的指数曲线模型、Bertalanffy曲线模型、Logistic曲线模型、Weibull曲线模型、Gompertz曲线模型、Usher曲线模型均为广义Usher模型的几种特例,通过选取不同的模型参数,广义Usher模型可以将现有的几个沉降预测模型统一起来。因此,广义Usher模型具有更强的适应性,能够更好地拟合实测数据。

2 模型参数确定的改进差分进化算法

设一般非线性模型参数优化问题为

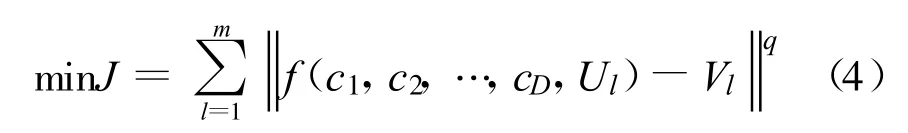
式中:J为优化准则系数;f为非线性系数模型输出值;c1,c2,…,cD为D个模型参数;Ul,Vl为m对输入、输出观测数据;q为任意实常数,工程上一般取q=2,即为通用的最小二乘法准则。

由于式(4)是一个非线性函数,因此该问题的参数确定是一个非线性参数的确定问题。可以采用许多方法,如高斯-牛顿或麦夸特法等,但这些传统的算法都对输入的模型参数初始值有一定的要求,若输入的参数值与参数的真实值偏离较大,可能造成迭代不收敛,而且也很难得到全局优化解。而进化算法如遗传算法[13]是目前处理一般非线性数学模型优化的一种新的优秀算法,它对模型是否线性、连续、可微等没有限制,也不受优化变量数目、约束条件的束缚,直接在优化准则函数(目标函数)的引导下进行全局自适应寻优,该方法直观、简便、通用、适应性强。因此可以用进化算法进行搜索,从而确定模型结构参数。

差分进化算法(DE算法)是Storn等[14]于1995年提出的一种较为简单、有效的进化算法。由于其原理简单,受控参数少,易于理解和实现,实施随机、并行、直接的全局搜索,已成为进化算法的一个重要分支。目前,DE算法已在优化应用方面取得了良好的效果[15]。考虑到已有较多文献研究证明DE算法优化性能优于遗传算法,这里采用笔者改进研发的DEPES算法来进行优化求解。下面给出DEPES算法求解沉降预测广义Usher模型的步骤[12]:

步骤1 构建目标函数:根据式(3)和式(4),由m对实测沉降观测数据{tl,sl}可构建待优化目标函数(累计残差平方和)如下:

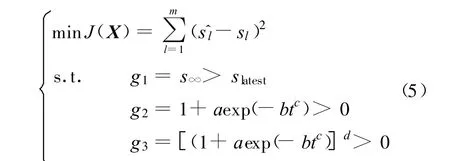
式中,X为列向量,X=[s∞,a,b,c,d]T;^sl为根据式(3)得出的沉降量计算值;g1为考虑极限沉降量s∞大于最后一次沉降观测值 s latest而设置的约束;g2,g3为使式(5)目标函数式有意义而设的约束。以上约束采用罚函数法进行处理。

步骤2 初始化种群:置当前进化代数G←1,利用预设的算法控制参数(种群中个体数量N p、交叉概率Cr、最大进化代数 Gmax、变量维数D)在变量下上限范围[XL,XU]内(问题可行域)随机初始化种群个体 Xi,G(i=1,2,…,Np)。

步骤3 种群评价:将种群个体代入式(5)计算出目标函数值,以确定最优目标函数值Vbf和相应的最优个体 X best。

步骤4 参数调整:随机产生差分进化模式集合DE/x/y/z(x表示在变异操作时,是随机选取当前代中某一个体Xrand,G作为父个体还是选择当前代中最优个体作为父个体 Xbest,G;y表示在变异操作时,所使用差分个体的个数;z表示交叉方案),作为第G代的差分进化模式;并在[0.2,0.9]范围内随机动态调整当前代的缩放因子F G。

步骤5 变异操作:对每个目标个体Xi,G,按步骤4确定的进化模式变异得到扰动个体 V i,G+1。

步骤6 交叉操作:根据 Xi,G和Vi,G+1按步骤4确定的相应进化模式交叉,生成新的试验个体U i,G+1。

步骤7 并行试验搜索:按式(6)产生新的试验个体Y i,G+1:

式中:Xbest,G为第G代的最优秀个体;σi,G,σi,G+1分别为父代、子代个体的标准差;σε,σi,0分别为标准差基数和初始标准差,应用中常取 σε=0,σi,0∈[1,3];随机实数A∈[1,10];N(0,1)为服从标准正态分布的随机数。

步骤8 变量边界约束处理:对不符合变量边界约束的新个体Ui,G+1,Yi,G+1,Xi,G用在可行域内产生的随机个体来代替。

步骤9 选择操作:将 Ui,G+1,Yi,G+1,Xi,G所对应的目标函数值进行比较,保留优秀解;更新 Vbf和X b est;置 G←G+1。

步骤10 判断是否收敛:若是,则结束算法,输出结果;否则,转入步骤4,直至满足收敛条件。

基于上述步骤,在Matlab软件环境中编制了相应的计算程序。下面结合实际工程的沉降观测数据,将DEPES算法应用于计算分析中。

3 工程实例计算分析

3.1 实例计算

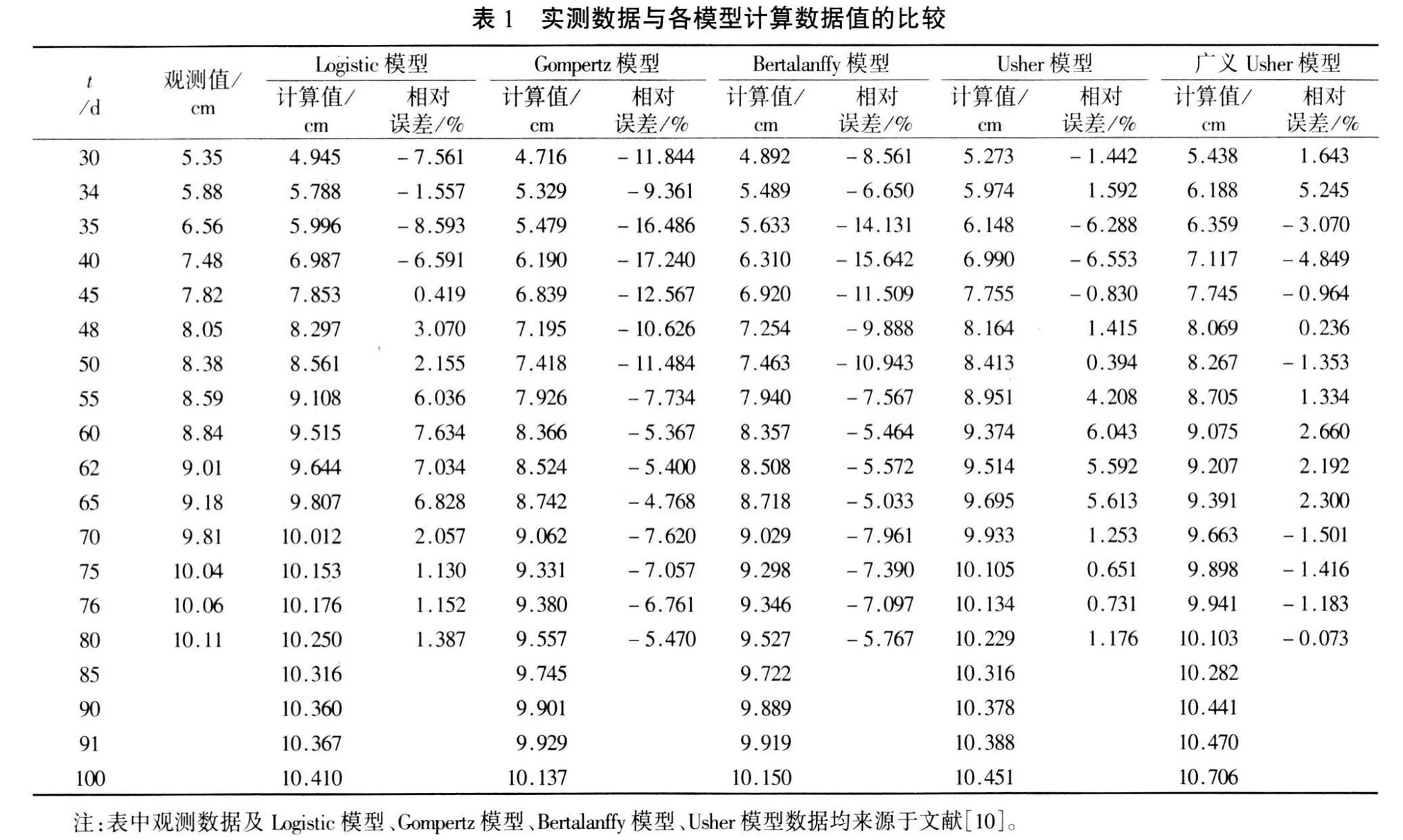
为便于比较几种常用预测模型的拟合预测情况,选用文献[10]中的实例为例,即宁杭高速公路工程。其NH标k95+520观测点的沉降观测资料如表1所示。沉降观测从2002年8月19日至12月14日止。现同样以该处沉降观测资料前80 d的沉降观测数据作为计算模拟值,用本文的广义Usher模型及DEPES算法对沉降数据进行模拟和预测。经编程并在计算机上实现,DEPES算法的参数设置为Np=50,Cr=0.5,Gmax=1000,Vf=10-6。利用DEPES算法进行若干次随机试验搜索,取最好的一组结果为 s∞=12.346,a=338.381,b=8.90529,c=0.106501,d=871.744。即广义Usher模型为

?

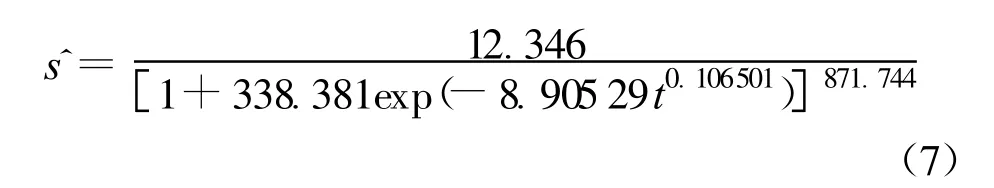
根据式(7)可计算出30～100 d的沉降模拟值和预测值,及相对误差对比情况,如表1所示,得出的沉降与时间关系曲线如图1所示。

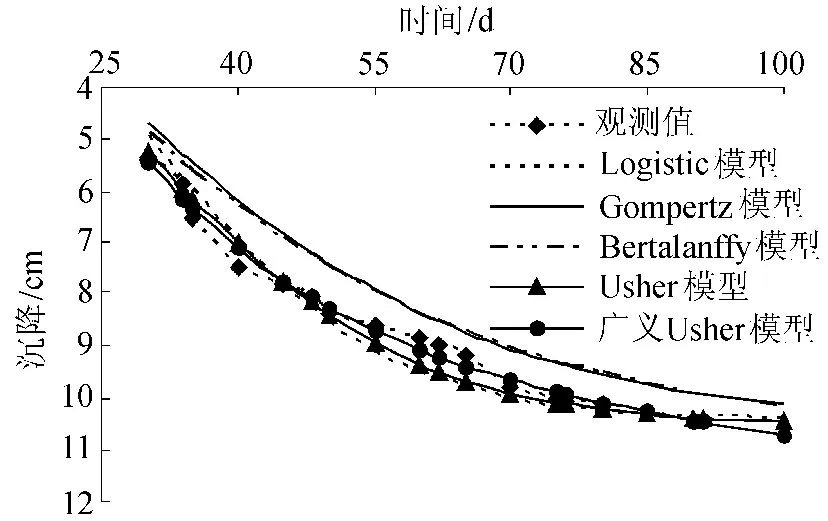
图1 实测曲线与各模型计算曲线的比较

3.2 讨论分析

为提高预测的精度,首先要保证有充分高的模拟精度,尤其是 t=80 d时的模拟精度。从表1可见,广义Usher模型在t=80 d时的沉降模拟值为10.103cm,与观测值10.11cm非常接近,相对误差的绝对值仅为0.073%,均小于表中所列其他模型相对误差绝对值;再从30～80 d的整体沉降模拟情况来看,本文方法使平均绝对值相对误差较小(2.001%),也均小于其他模型平均绝对值相对误差。表2为各模型评价指标,表2中,无论是从相关指数还是从累计残差平方和等评价指标来看,广义Usher模型的模拟和预测效果都是最佳的。以上分析表明,广义Usher模型能更好地适应实际情况的变化,可以获得很高的拟合精度,其推算的结果是可靠的。

表2 各模型评价指标

对于DEPES算法和DE算法的优化搜索性能比较,图2、图3绘出了该次算法试验搜索的进化过程曲线。图中纵坐标采用对数坐标。由图2可见,当各算法在处理如本文这一含有多变量、带约束的较复杂非线性优化模型时,DE算法表现欠佳,而DEPES算法较为理想,DEPES算法所对应的最优目标函数值下降曲线比DE算法的下降曲线具有更快的下降速度和更好的下降程度。这说明DEPES算法比DE算法具有更快的收敛速度和更好的收敛精度。为便于观察各算法前期进化搜索情况,结合图2,从图3绘出的算法前200代进化过程曲线可见,DEPES算法大约在120代左右就可以收敛到问题的满意解,而DE算法却在给定的进化代数1000代内仍未能收敛至DEPES算法的计算结果。综上所述,DEPES算法可快速收敛至高精度解,是DE算法的一种有效改进算法。

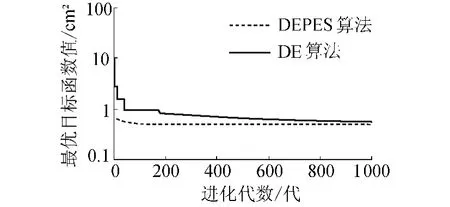
图2 各算法整体搜索过程的进化曲线

图3 各算法进化200代的进化曲线

4 结 论

a.通过对软土路基沉降预测广义Usher模型分析,常用的指数曲线模型、Logistic模型、Gompertz模型 、Bertalanffy模型 、Weibull模型 、Usher模型等 6 种沉降预测模型均为其特例,该模型具有更强大的可塑性和适应性,可获得较其他模型更高精度的沉降模拟预测值。

b.给出了沉降预测广义Usher模型参数优化求解的改进差分进化算法,该算法具有计算速度快、自动化程度高、通用性强等特点,是一种有效的智能优化算法,适用于非线性优化问题的数值优化求解,可在其他岩土工程非线性优化问题中推广应用。

[1]吴钰,徐泽中,陈景扬.不同方法估算路基最终沉降量的分析研究[J].水利水电科技进展,1998,18(2):17-21.

[2]王伟,宰金珉,卢延浩.软土工后沉降双曲线模型与指数曲线模型分析[J].江苏大学学报:自然科学版,2008,29(2):173-176.

[3]冯文凯,刘汉超.修正双曲线法在路基沉降变形初期阶段的应用探讨[J].地质灾害与环境保护,2001,12(3):61-63.

[4]张仪萍,俞亚南,张土乔,等.沉降预测中的灰色模型理论与Asaoka法[J].系统工程理论与实践,2002(9):141-144.

[5]方宝.星野法在某软基段沉降预测中的应用[J].科技创新导报,2009(17):53-54.

[6]梅国雄,宰金珉,殷宗泽,等.沉降～时间曲线呈 S形的证明及其应用:从一维固结理论角度[J].岩土力学,2004,25(1):20-22.

[7]朱志铎,周礼红.软土路基全过程沉降预测的Logistic模型应用研究[J].岩土工程学报,2009,31(6):965-969.

[8]余闯,刘松玉.路堤沉降预测的Gompertz模型应用研究[J].岩土力学,2005,26(1):82-86.

[9]王伟,卢廷浩.基于Weibull曲线的软基沉降预测模型分析[J].岩土力学,2007,28(4):803-806.

[10]赵明华,龙照,邹新军.路基沉降预测的Usher模型应用研究[J].岩土力学,2008,29(11):2973-2976.

[11]李社文.广义Usher模型的建立及其在油田生产中的应用[J].新疆石油地质,2001,22(2):133-135.

[12]许小健,张金轮.基于并行优进策略的差分进化算法[J].厦门理工学院学报,2009,17(3):73-78.

[13]金菊良,杨晓华,丁晶.基于实数编码的加速遗传算法[J].四川大学学报:工程科学版,2000,32(4):20-23.

[14]STORN R,PRICE K.Differential evolution:a simple and efficientheuristic forglobaloptimization over continuous space[J].Journalof Global Optimization,1997,11(4):341-359.

[15]许小健,涂芬芬,黄小平,等.差异演化算法在 Van Genuchten方程参数优化估计中的应用[J].合肥工业大学学报:自然科学版,2008,31(11):1863-1866.