李文华 李盛恩

(山东建筑大学计算机科学与技术学院 山东 济南 250100)

0 引 言

随着移动智能终端和移动互联网的普及,越来越多的业务和互联网紧密结合起来。从社交网络到智慧政务,从餐饮娱乐到智能交通,人们在享受互联网+带来的无限便利的同时,每天也产生了海量的数据。这些数据具有以下特点:(1) 数据量大,存储单位从过去的GB、TB级到现在的PB乃至EB级别。(2) 数据结构多样,大量数据为无结构化数据、半结构数据。(3) 数据产生速度快,对网络传输的性能要求高,有些数据需要实时处理,对服务器的计算处理能力要求高。(4) 数据价值密度低[1]。

面对这些数据,传统的关系型数据库在处理时显得力不从心。为了更好地存储和管理这些数据,各种新型数据库应时而生。以Neo4J为代表的图数据库就是其中的一类,它以属性图作为逻辑存储模型,凭借图的独特构造,在存储和管理如社交网络、生物信息网络、智能交通网络等数据时发挥了重要作用。

在数据库系统中,快速准确地进行查询是用户的一项基本需求,为了满足用户的这一需求,传统数据库的设计和开发者为数据建立了各式各样的索引,极大提高了查询效率,现在已经非常成熟。而图数据中的查询种类众多,包括可达性查询、最短路径查询、关键字查询、匹配查询等,近年来,针对这些查询的研究得到了更多学者的关注。

可达性查询研究的是图中两个顶点之间是否存在可达路径,作为图数据管理中使用最频繁的操作,可达性查询在子图匹配查询、生物信息学、社交网络等领域中应用广泛[2-3]。但是对于一些现实中的问题,仅仅进行可达查询并不能满足用户的需求,如在无线传感器网络、互联网、电信网以及社交网络中,顶点u对顶点v的影响力受制于从u到v的路径长度(例如无线传感器网络的广播消息可能在传输过程中的任何一步丢失,其他顶点接收到的概率会随着路径长度的增加以指数级速度衰减)[4],因此针对K步可达性查询的研究逐渐增多。K步可达性查询是在可达性查询的基础上,对两顶点间的路径长度限制至K,即回到两点间是否存在一条长度不超过K的路径。K步可达性查询相比可达性查询,不仅能反映顶点间是否存在影响,还能反映顶点间的影响程度,可以提供更多有用信息,在无线传感器网络、互联网、电信网以及社交网络等实际应用中应用广泛,具有较高的实用价值。

近年来,随着研究的深入,已有多个K步可达性查询算法先后被提出,但是这些算法的研究对象均为无权图。而在一些现实问题中,我们要处理的往往是带权重的图数据,如前文提到的传感器网络、社交网络、交通网络等,在这些网络中,权重可以表示传感器间的距离、功率损耗,社交网络中人与人之间的亲密程度,交通网络中两城市间的距离、油耗等。此外,有些算法的研究对象限定为有向无环图,如果图数据中存在环,则通过压缩强连通分量构造为有向无环图,这在K步可达性查询中并不合理;有些算法在构建索引时需提前指定查询步数K,且针对每个K构建的索引只适合K步以内的查询,在查询时不能灵活地更改查询步数K。

针对以上问题,本文提出了一种针对带权有向图的K步可达性查询算法,能在常数时间内完成大部分K步可达性查询。具体来说,本文的贡献如下:(1) 根据现实问题,提出了带权有向图上的K步可达性查询,以双向最短路径索引和K-Reach索引为基础设计了高效索引,能在常数时间完成大部分K步可达性查询。(2) 研究对象不再局限于有向无环图,对于带环图也可以正常处理;构建索引时,不需要提前指定查询步数K,并且在查询时可以灵活改变查询步数K。(3) 基于多个真实图数据进行测试,通过与无权图上的K步可达性查询算法对比,实验结果表明本文算法高效可行。

1 背景知识和相关工作

1.1 背景知识

本文的研究对象为带权有向图G=(V,E),其中V是G的顶点集合,V中的顶点用u、v等小写英文字母表示,E是G的有向边集,E中的有向边用(〈u,v〉,w)表示,其含义是从u到v的一条有向边,w为边上权重。IN(u)表示指向顶点u的顶点集,OUT(u)表示顶点u指向的顶点集,wpath(u,v)表示从u到v的路径长度,即从u到v所经过边的权重之和。

本文要处理K步可达性查询,即查询给定的图G中的两个顶点u和v,是否存在一条从u到v且长度不超过K的路径,若存在,则称uK步可达v,用u→kv表示。若不存在,则称uK步不可达v,用u→/kv表示。

1.2 相关工作

根据索引类型进行分类,可将目前已有的K步可达性查询算法分为两类。第一类是基于可达性的K步可达性查询算法,该类方法的基本思想是以可达性查询结果作为否定剪枝条件,如果通过可达性查询判断出两顶点u和v不可达,则两顶点一定K步不可达;如果可达性查询结果为可达,则结合辅助索引做进一步判断。第二类基于顶点覆盖集的K步索引方法,其基本思想是首先求出原图的一个顶点覆盖集,然后根据原图中的可达性,在顶点覆盖集上建立K步可达索引。在查询时,根据顶点u和v是否属于顶点覆盖集,将查询分为四种情况,再利用建立的索引实现快速查询。

1.2.1基于可达性的K步可达性查询算法

基于可达性的K步可达性查询算法以可达性查询为基础,在构建索引时,首先通过压缩强连通分支,将原图转换为有向无环图,然后在有向无环图上构建可达性查询索引和一些辅助索引。在查询时,该类方法以可达性查询结果作为否定剪枝条件,首先通过可达性查询判断出两顶点u和v是否可达,如果不可达,则两顶点一定K步不可达;若可达,则利用辅助索引进一步判断,若通过辅助索引的查询结果为不可达,则两顶点一定K步不可达,若辅助索引的结论果仍为可达,则依次判断以顶点u的为弧尾的相邻顶点集中的点是否K-2步内可达以顶点v为弧首的相邻顶点集中的点,若是,则u可以K步可达v,否则u不可K步可达v。该类方法的典型代表有BiRch算法[4-5]、kRH算法[6]、BFSI算法[7]、RE-GRAIL算法[8]。

BiRch算法以著名的可达性算法GRAIL[9,10]为基础,其基本思想是:首先对有向无环图分别进行从左到右和从右到左的后根遍历,每个顶点两次后根遍历的次序分别作为其两个区间的上界post,而区间的下界为其子节点区间的下界的最小值min,若该顶点为叶子节点,则其区间下界和上界相等,这样就构建起单向双区间的可达性索引。为了加速查询,该算法索引中还包含了每个顶点的双向广度层数和双向拓扑层数。在查询时,首先根据可达性查询判断两点是否可达,如果不可达,则得出结论,两点K步不可达,否则,利用双向广度层数和双向拓扑层数进行判断,若仍不能判断出结果,则递归地从两顶点出度或入度较小的一侧向另一侧查找,递归结束的条件是递归次数达到K或查到另一个顶点。

kRH算法以PLL算法[11-13]为基础,其基本思想是为部分度大的顶点构建双向最短路径索引。首先选取部分度大的顶点(这些点称为HOP点),根据实验,当一幅图中选择的度大的节点数达到32个时,要么这些节点维护的可达性信息已经足够多,要么再增加节点也不会显著增加可达性信息。然后利用广度优先遍历为这些HOP顶点分别建立两个标签LIN和LOUT(u),前者存储图中可达u的顶点及其到u的路径长度,后者存储u可达的顶点及其路径长度。为了快速判断不可达,本文在索引中为非HOP点添加了正反互逆拓扑号。在查询时,对于给定的点u和v,如果至少有一个为HOP点,则直接查找其与另一个点的路径长度,判断路径长度是否小于或等于K,若是则两点K步可达,否则K步不可达;若两点均不为HOP点,则利用正反互逆拓扑号进行判断,若判断结果为不可达,则说明两点K步不可达,否则借助原图递归地从两顶点出度或入度较小的一侧向另一侧查找,直到递归次数达到K或查到另一个顶点。

BFSI算法以GRIPP[14]和FELINE[15]算法为基础,首先利用可达性算法构建FELINE索引,然后将原图生成广度优先森林,对广度优先森林中的每一个棵树进行后根遍历,构建min-post间隔标签索引,最后对每棵树进行广度优先遍历,得到每一个顶点的全局广度层数。在查询时,对给定的两点u和v,步长K,先利用FELINE索引进行可达性查询,如果查询结果为两点不可达,则得到两点一定K步不可达,否则利用min-post索引的包含关系进行判断;如果点u的min-post间隔标签包含点v的标签,则判断u的全局广度层数减点v得到的值是否小于步长K,如果是,则两点K步可达,否则不可达;如果点u的min-post间隔标签不包含点v的标签,则从点u的出度和点v的入度两者中小的一侧进行递归的搜索,直到得出结论。

RE-GRAIL算法同样以可达性算法GRAIL[9-10]为基础,结合文献[16]中的算法。在构建索引时,首先对有向无环图进行从左到右的后根遍历,为每个顶点构建一个区间,然后将有向无环图反向再进行一次从左到右的后根遍历,为每个顶点再构建一个区间,这样就构建起了双向双区间标签索引。在查询时,对于给定的两点u和v,仍然是先根据可达性查询判断两点是否可达,如果不可达,则一定K步不可达,否则递归地判断u的子节点是否K-1步可达v直到得到结果。

基于可达性的K步可达性查询算法,充分利用可达性查询,巧妙地结合一些剪枝策略,算法简明清晰,然而在实际中,顶点之间或多或少存在某种联系,可达性查询大多会返回肯定的结果[17],因此剪枝效果并不理想。并且其研究对象为有向无环图,这并不符合实际应用情况,在可达性查询中,因为强连通分支内顶点都是相互可达的,可以通过压缩强连通分量,将普通有向图转为有向无环图,但在K步可达性查询中,压缩强连通分支变得不合理,比如在K步可达性查询中重要应用交通路网中,如果假设路网为有向无环图,那么意味着从一个城市出发即再也无法回到该城市,这显然不符合常理。

1.2.2基于顶点覆盖集的K步索引方法

文献[18-19]提出了基于顶点覆盖集的K步索引方法K-Reach,该方法的基本依据是一条边的两个顶点,至少有一个在顶点覆盖集中。在构建索引时,该方法首先要确定查询步数K,然后对给定的图G求近似最小顶点覆盖集S,求出顶点覆盖集S中顶点在原图中的所有路径及长度,将路径长度不超过K的路径和路径长度作为带权有向边,保存为索引,此外索引中还包含近似最小顶点覆盖集S,所以该方法的索引由顶点集S和带权有向边集构成。在查询时,对于给定的两个顶点u和v是否在顶点覆盖集S中,将查询分为四种情况,当u和v均属于顶点覆盖集S时,直接查询〈u,v〉的路径长度并与K值进行大小比较,若路径长度小于或等于K值,则u可以K步可达v,否则u不可K步可达v;当u属于顶点覆盖集S,但v不属于S时,依次取IN(v)中的顶点t,因为v不属于S,所以t一定属于顶点覆盖集S,所以直接查询〈u,t〉的路径长度并与K-1进行大小比较,若路径长度小于或等于K-1,则u可以K步可达v,否则u不可K步可达v;当u不属于顶点覆盖集S,但v属于S时,依次取OUT(u)中的顶点s,因为u不属于S,所以s一定属于顶点覆盖集S,所以直接查询〈s,v〉的路径长度并与K-1进行大小比较,若路径长度小于或等于K-1,则u可以K步可达v,否则u不可K步可达v;当u和v均不属于顶点覆盖集S时,依次取OUT(u)中的顶点s和IN(v)中的顶点t,查询〈s,t〉的路径长度并与K-2进行大小比较,若路径长度小于或等于K-2,则u可以K步可达v,否则u不可K步可达v。

K-Reach方法的研究对象不再局限于有向无环图,利用指定K值构造出来的索引,也能提供较好的查询效率,但是其仍不能解决带权图上的K步可达性查询,同时构造索引时需要提前指定K值,查询时K值不能灵活更改等问题使得该算法难以在实践中应用。

2 基本思想和算法描述

2.1 索引构建算法

本文提出的针对带权有向图的K步可达性查询算法,首先求解给定图的近似最小顶点覆盖集,然后基于顶点覆盖集构建索引,类似于文献[15]提出的算法,与之不同的是,本文的研究对象由简单有向图变为带权有向图,在构建索引时也不需要提前指定K值。除了顶点覆盖集上的索引外,为了避免在查询过程中的I/O操作,提高查询效率,本文还构建了顶点覆盖集外的双向最短路径索引。

2.1.1求解近似最小顶点覆盖集

根据文献[20]的证明,最小顶点覆盖问题属于NPC类问题,通常一个问题若被证明为NPC类,人们认为该问题不能在多项式时间内解答。虽然无法准确求解图的最小顶点覆盖集,但是可以在多项时间内求解图的近似最小顶点覆盖集。文献[15]给出了一个求解近似最小顶点覆盖集的朴素算法,即从边集中任选一边〈u,v〉,将该边的两顶点u、v依次加入到顶点覆盖集S中,然后将顶点u或v能覆盖到的边从边集中全部删除,重复上述过程,直到边集为空,这样就得到了一个顶点覆盖集。该算法简单易懂,但得到的顶点覆盖集往往规模偏大。本文采用贪心算法来求解近似最小顶点覆盖集,首先计算图中各顶点的度,选出度最大的顶点,然后将该顶点加入到顶点覆盖集中,并将该顶点覆盖到的边从边集中全部删除,在删除过程中,对相关顶点的度进行调整,重复上述过程,直到边集为空。具体如算法1所示。

算法1近似最小顶点覆盖集算法

输入:带权有向图G=(V,E)

输出:近似最小顶点覆盖集S

1. /*初始化各顶点的度*/

2. for each nodeuinVdo

3. Array[u]←getdegree(u)

4. /*求近似最小顶点覆盖集*/

5. WhileEis not empty do

6. findvwhich has biggest degree

7. addvintoS

8. for each nodesin OUT(v) or IN (v) do

9. delete( or )

10. Array[s]—

需要说明的是,在求解近似最小顶点覆盖集的过程中,因为边的方向和权重不起作用,我们可以将其暂时忽略。如图1所示,最小顶点覆盖集由灰色顶点构成。

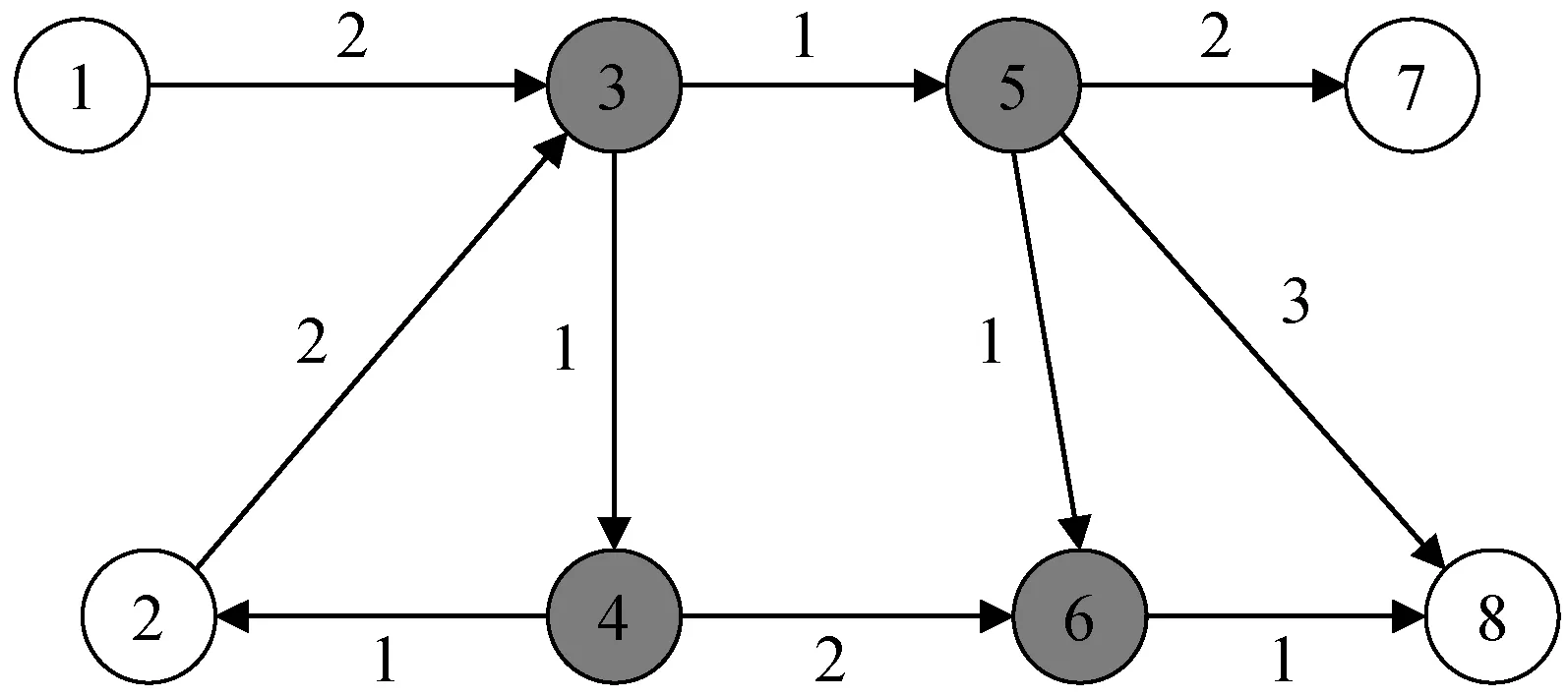
图1 带权有向图G(灰色点构成顶点覆盖集S)

本文采用的求解近似最小的顶点覆盖集的贪心算法的时间复杂度为O(mn),不如文献[15]给出的朴素算法时间复杂度O(m+n),但该算法求解的顶点覆盖集更小,有利于保证接下来的索引构建过程的时间和空间效率。

2.1.2构建索引

基于上一节得到的近似最小顶点覆盖集,进行索引构建,具体如算法2所示。最终构建的索引由三部分构成,分别是近似最小顶点覆盖集S、S内索引和S外索引。其中近似最小顶点覆盖集S已经求出,可直接加入到索引中。

算法2索引构建算法

输入:带权有向图G=(V,E)。

输出:Index=(S,Es,Eout)。

1./*求近似最小顶点覆盖集*/

2.Compute the approximate min vertex coverS

3.*求S内顶点间的最短路径*/

4.for each nodeuinSdo

5.ComputeEs={(,w)|v∈S,w=wpath(u,v)}

through BFS(u,G)

6./*求S外的索引*/

7.for each nodeunot inSdo

8.for each nodevinOUTI(u) do

9.u.outadd(v,w)

10.for each nodevinINI(u) do

11.u.inadd((v,w)

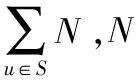
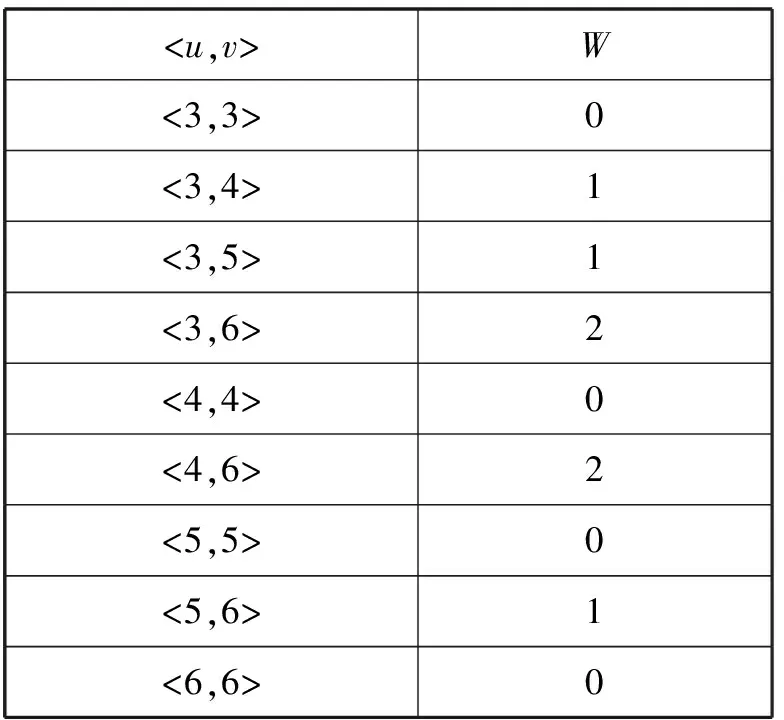
表1 顶点覆盖集S内索引

S外索引类似于kRH算法中的双向最短路径索引,具体构建过程如下,对S外的每一个顶点u,依次访问OUT(u)或IN(u)内顶点v,因为u不属于S,所以v一定属于S,将(v,w)加入到S外索引的OUTI(node,weight)或INI(node,weight)中。最终构建的S外索引如表2所示。S外是该索引的重要组成部分,借助该部分,本算法可以实现在不访问原图的情况下,完成K步可达查询操作。虽然该部分索引在一定程度上增大了索引的规模,但是有效避免了I/O操作,大幅提高了查询效率。通过分析易知,其时间复杂度为|V-S|max{|OUT(u)|,|IN(u)|}。

表2 顶点覆盖集S外索引

2.2 查询处理

对于给定的两顶点u、v和路径长度K,根据u和v是否属于近似最小顶点覆盖集S,将查询分为四种情况:(1) 若u和v均属于S,则直接查询S内索引得到wpath(u,v),若wpath(u,v)≤K,则uK步可达v,否则uK步不可达v。(2) 若u属于近似最小顶点覆盖集S,而v不属于S,则首先判断S外索引中的v的入边顶点集INI(v)是否为空,若INI(v)为空,则uK步不可达v,否则依次遍历顶点v的入边顶点集INI(v)中的点t,判断是否存在t使得wpath(u,t)+get(t)≤K,若存在这样的点t,则uK步可达v,否则uK步不可达v。(3) 若u不属于近似最小顶点覆盖集S,而v属于S,同样首先判断S外索引中的u的出边顶点集OUTI(u)是否为空,若OUTI(u)为空,则uK步不可达v,否则依次遍历顶点u的出边顶点集OUTI(u)中的点s,判断是否存在s使得wpath(u,s)+get(s)≤K,若存在这样的点s,则uK步可达v,否则uK步不可达v。(4) 若u和v均不属于顶点覆盖集S,则首先判断S外索引中的u的出边顶点集OUTI(u)或v的入边顶点集INI(v)是否为空,若二者任意一个为空,则uK步不可达v,否则依次遍历顶点u的出边顶点集OUTI(u)中的点s和顶点v的入边顶点集INI(v)中的点t,判断是否存在点s和点t使得get(u)+wpath(s,t)+get(v)≤K,若存在这样的点s和t,则uK步可达v,否则uK步不可达v。具体如算法3所示。

算法3查询算法

输入:Index=(S,Es,Eout);顶点u和v,步长K。

输出:True of False。

1./*顶点uv均属于S*/

2.if (u∈Sandv∈S)

3.d=getwpath(u,v)

4.if (d<=K) return true

5.else return flase

6./*顶点u属于S,v不属于*/

7.if (u∈Sandv∉S)

8.ifINI(v) is empty return false

9.for (tinINI(v))

10.d=getwpath(u,t)+get(t)

11.if (d<=K) return true

12.else return false

13./*顶点u不属于S,v属于*/

14.if (u∉Sandv∈S)

15.ifOUTI(u) is empty return false

16.for (sinOUTI(u))

17.d=getwpath(u,s)+get(s)

18.if (d<=K) return true

19.else return false

20./*顶点u和v均不属于S*/

21.if (u∉Sandv∉S)

22.ifOUTI(u) orINI(v) is empty

return false

23.for (sinOUTI(u))

24.for (tinINI(v))

25.d=get(s)+getwpath(s,t)

+get(t)

26.if (d<=K) return true

27.else return false

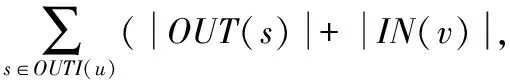
例如要查询图1中的顶点2和5是否3步内可达,因为顶点3不在顶点覆盖集中,而顶点5在,所以首先判断顶点3的出边顶点集是否为空,发现顶点3的出边顶点集不为空且由顶点4构成,所以根据S外索引得到get(4)=1,根据S内索引得到wpath(4,5)=2,两者求和得到的路径长度为3,与给定的步长相等,所以顶点2,3步可达顶点5。

3 实 验

3.1 实验环境和实验数据

本实验所用的计算机配置为Pentium(R) Dual-Core CPU E6600处理器,主频3.06 GHz,8 GB内存,500 GB机械硬盘,Windows 10教育版操作系统。本实验所用算法均由Java语言实现,JDK版本为1.8.0_181。

本文选取了K步可达性查询中常用的10个数据集,用于性能测试,包括FAA、FIGEYS、OpenFlights、DBLP、Linux、Google Plus、CornCitation、Ego_Twitter、USAirport、MorenoHealth,这些数据全部来自科布伦茨网络数据集(http://konect.uni-koblenz.de/),其中FAA、OpenFlights、USAirport是航空路网,DBLP、CornCitation、Linux是引用网络,Google Plus、Ego_Twitter、MorenoHealth是社交网络,FIGEYS是人类蛋白质网络。FAA、DBLP、Linux网络中存在回路。OpenFlights、Linux、USAirport、MorenoHealth为平均度超过10的稠密图。USAirport和MorenoHealth网络中自带权重信息,其他网络中权重由本文利用随机函数添加。各数据集的统计信息如表3所示,其中|V|代表图中顶点数,|E|代表边数,Average Degree为各顶点的平均度数。

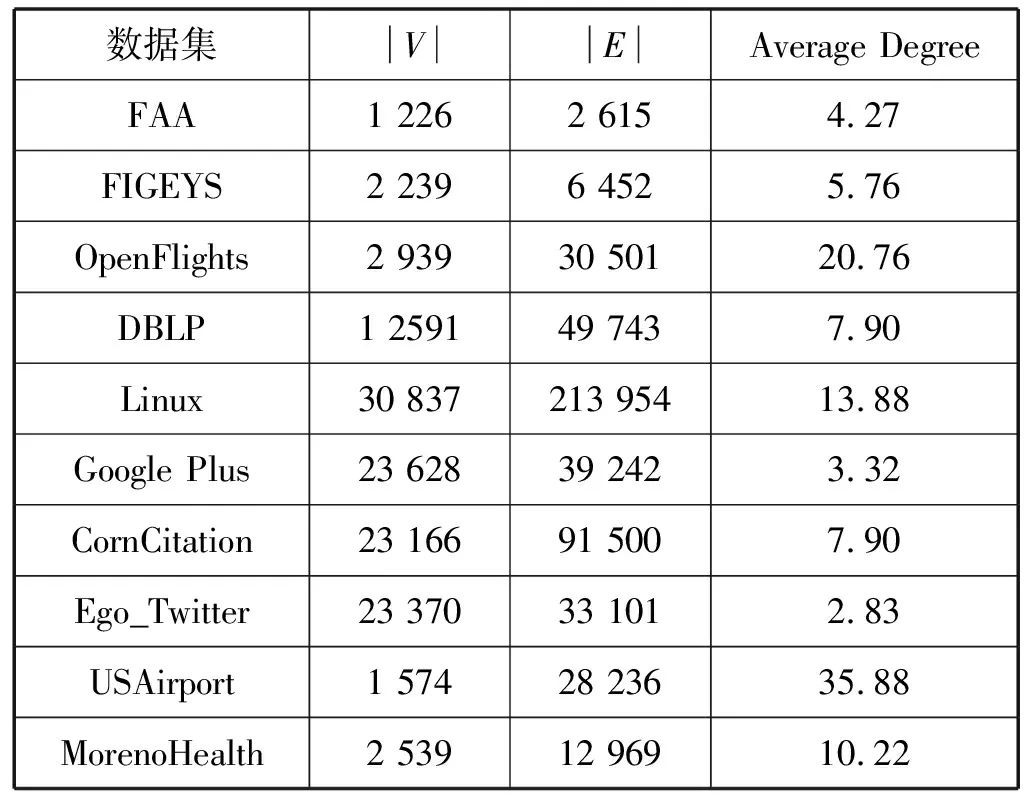
表3 数据集统计信息

因为目前还没有针对带权有向图上的K步可达性查询算法,同时考虑到大部分已有算法的处理对象为有向无环图,可比性不强,本文选择与可以处理带环有向图的K-Reach算法进行比较,其中参数K设为10,通过索引构建时间、索引规模、查询时间三个指标进行性能评价。本文所列出的所有数据均为算法执行10次的平均值并通过四舍五入保留到小数点后两位,表中KRAWG为本文中提出的算法。

3.2 索引构建时间和规模

表4给出了两种算法所求的顶点覆盖集规模,通过比较发现,采用优先选择度大顶点的贪心算法求解得到的顶点覆盖集规模明显小于朴素算法得到的顶点覆盖集规模,平均降低约35%。

表4 顶点覆盖集规模

表5给出了两种算法的索引构建时间,从索引构建时间可以发现,在稀疏图上,KRAWG算法与K-Reach的相比略占上风,但差别不大。但在稠密图上,KRAWG算法的优势比较明显,索引构建时间平均降低约50%。这主要得益于KRAWG算法在求解近似最小顶点覆盖集时采用了优先选择度大顶点加入顶点覆盖集的贪心算法,有效降低了顶点覆盖集中顶点数量,从而减少了构造比较费时的顶点覆盖集内索引规模,提高了索引构建效率。

表5 索引构建时间 单位:ms

表6给出了两种算法构造的索引规模,从索引规模来看,两种算法不相上下,KRAWG算法整体具有一定优势,主要是因为随着顶点覆盖集内索引规模的减少,顶点覆盖集外索引规模逐渐上升,所以索引总规模保持相对稳定。

表6 索引规模

3.3 查询时间

表7给出了两种算法在步长K=10时,随机生成1万个顶点对进行查询的结果,表中数据为1万次查询时间之和。可以发现,在查询时间方面,两种算法效率相当,虽然KRAWG算法在查询过程中需要计算路径长度,但有限次的简单算术计算并不影响算法整体查询效率。

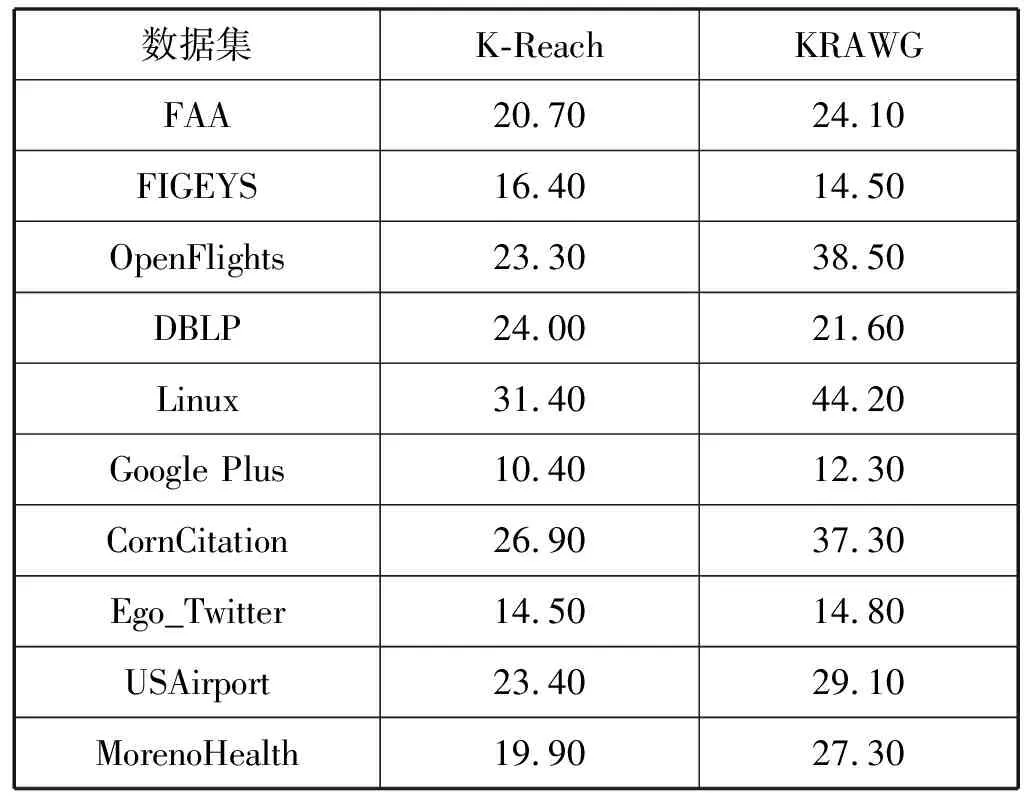
表7 查询时间 单位:ms

表8给出了KRAWG算法在K值分别为5、10、15时的查询时间,可以发现K值的变化对于算法的查询时间影响不大,这是因为KRAWG算法在顶点覆盖集上构建的索引与K值无关,不论K值如何变化,查询操作不会变化。

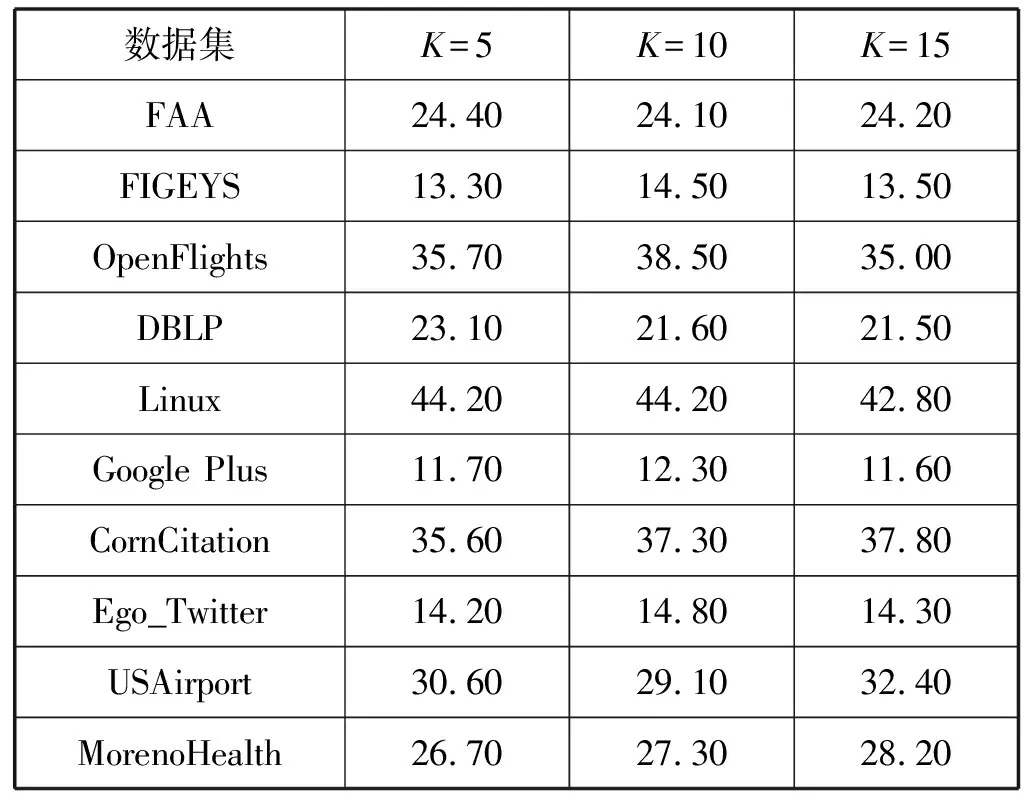
表8 不同K值的查询时间 单位:ms

4 结 语

本文针对K步可达性查询在实际应用中存在的问题,吸收已有K步可达性查询算法——K-Reach算法和KRH算法的优势,提出了带权有向图上的K步可达性查询算法KRAWG,并通过实验验证了算法的高效性。带权有向图上的K步可达性查询因为涉及到权重,需要额外空间进行存储,索引规模相对较大,如何在保证查询效率的前提下,尽可能压缩索引空间,值得进一步研究。