王爱民，金 浩，宋雪丽

（西安科技大学 理学院，西安 710054）

0 引言

近年来，Ratio 统计量是一种流行的检验时间序列变点问题的方法，其与传统的累计和方法相比不需要方差的估计。Horváth 等（2008）[1]运用Ratio 统计量检验短记忆的均值变点问题；Shao（2011）[2]、Kai 等（2018）[3]和Wingert 等（2020）[4]进一步研究了长记忆变点问题；Chen 等（2016）[5]运用Ratio统计量检验从短记忆到长记忆的变点问题。

实际上，上述文献大多考虑方差有限的情形。然而，方差无穷序列的大部分信息滞留在尾部，不能用传统高斯序列来刻画，所以本文针对方差无穷AR(p)序列检验结构变点。假设yt由下列模型产生：

其中，xt=(1,t,…,tp)T，β=(β0,β1,…,βp)T，p是大于等于0 的整数。εt是p阶自回归序列，新息过程ηt位于稳定吸收域。有：

参数κ（尾指数）控制尾部分布的厚度是未知的。式（3）和式（4）表明存在aT和bT使得：

先假设bT=0，κ>1，此时E(ηt)=0。特别地，当ηt是独立同分布的序列时，Kokoszka和Wol（f2004）[6]已证明：

本文拓展了Jin等（2009）[7]和Wang等（2016）[8]的理论，把独立同分布的新息过程延伸到弱相依的AR（p）情形；探索用ηt新息替代εt从而获得准确的临界值。虽然Perron和Zhu（2005）[9]以及Yang（2017）[10]提出了对趋势变点位置的估计，但是少有学者关注其检验问题，为此，本文考虑了厚尾AR（p）相依序列趋势变点的检验问题。

1 模型与修正Ratio检验统计量

假设y1,…,yT满足模型（1）和模型（2）。考虑p=1，即xt=(1,t)T。当p=0 时，模型退化成含有常数项的均值变点模型，本文不做研究。对于更一般的情况，xt=(1,t,…,tp)T,p≥2 仍然有效。在引入变点模型之前，为满足渐近有效性需提出如下假设：

假设1：假设1-ρ1z-…-ρpzp=0 所有的特征根都在单位圆外。

假设2：新息过程ηt是独立同分布的，在吸收域κ∊(1,2)且E(ηt)=0。

假设1 说明AR(p)过程可以表示为无限阶移动平均过程。假设2保证式（6）的中心极限定理存在，从而下列的Ratio 统计量有准确的极限分布。考虑新息过程为AR(p)的趋势变点模型：

其中，εt是厚尾AR(p)序列，1{∙}是示性函数，k*是趋势变点位置。ρi=0,i=1,…,p,模型退化为文献[8]及文献[11]的模型。原假设和备择假设下的检验问题为：

2 主要结论

本文给出检验趋势变点在原假设下的极限分布和备择假设下的一致性。为了方便起见，令v=k/T,s=i/T,v*=k*/T。

定理1：假设yt由式（8）生成，εt是厚尾AR（p）序列。若原假设H0、假设1和假设2成立，则当T→∞时，有：

证明：计算yt(t=1,…,k)对μ和β回归的最小二乘估计残差：

结合式（13）至式（15），得到统计量原假设下的极限分布为：

定理2：假设yt由式（8）生成，εt是厚尾AR（p）序列。若备择假设H1、假设1 和假设2 成立，当T→∞时，Ξ=R(k*)，有：

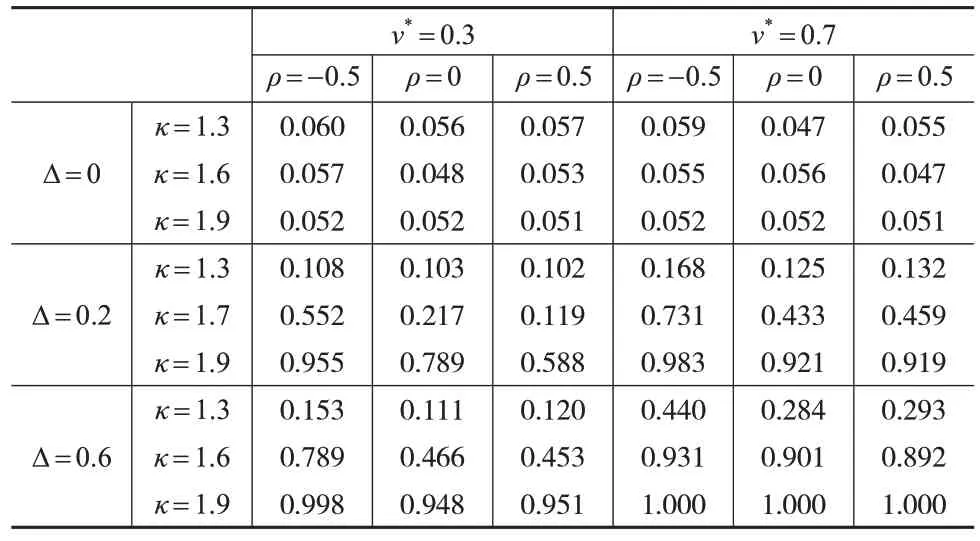
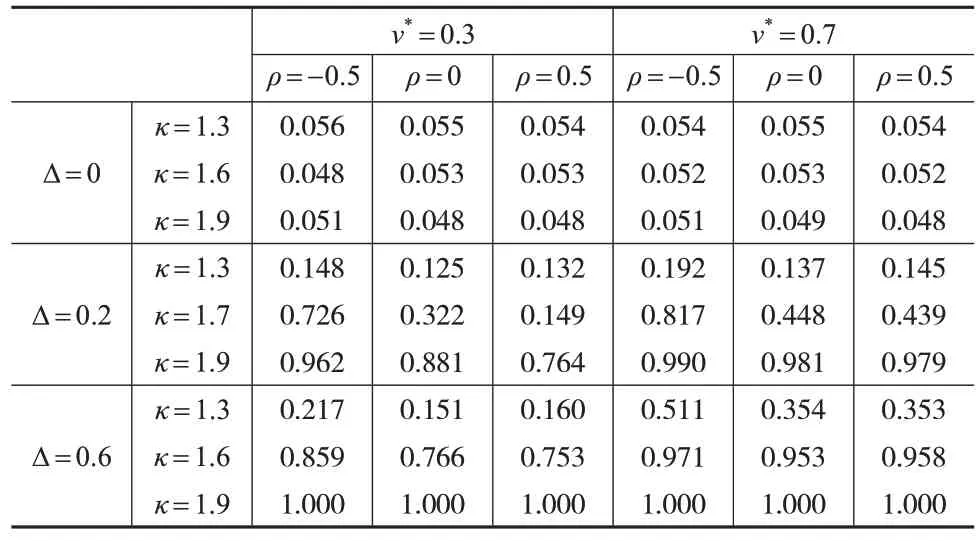
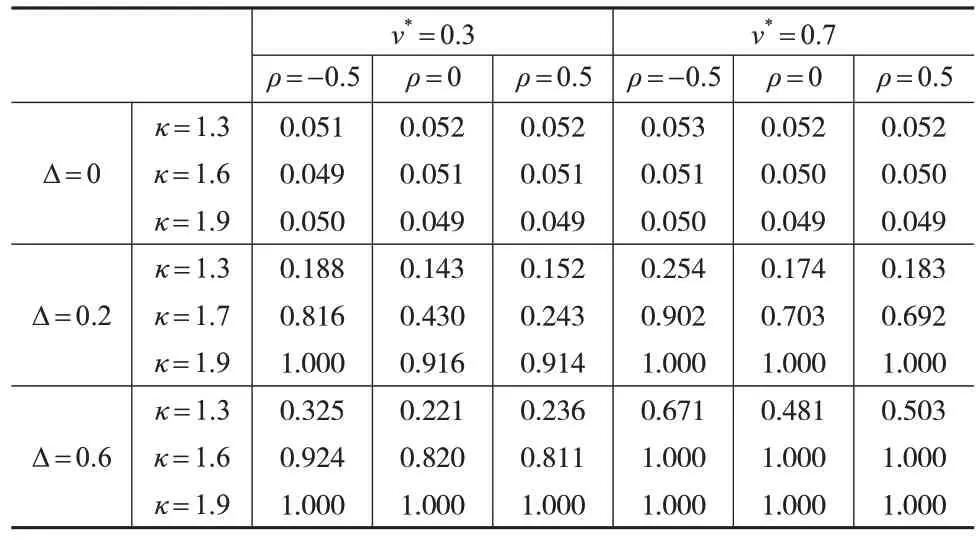
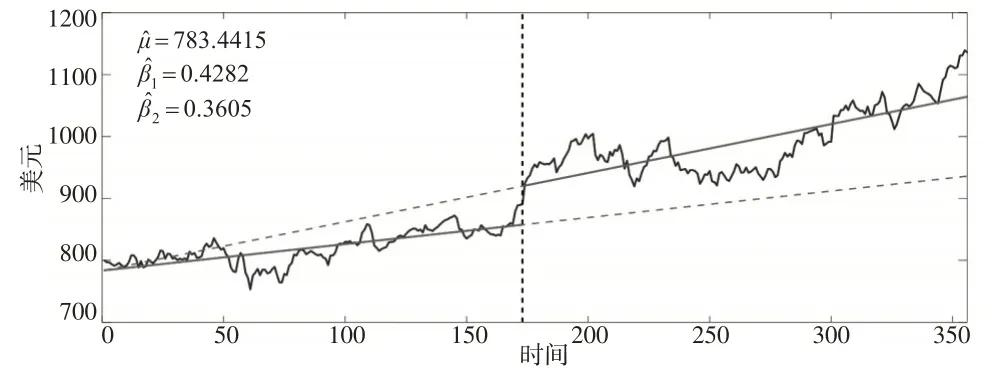
证明：若k

从而得到分母第二项的发散速度：

3 Subsampling抽样

因为趋势变点的极限分布依赖于尾指数κ，目前已有一些关于尾指数估计的文献，比如Koedijk 等（1990）[12]和Resnick（2007）[13]的研究，但其准确性不是很好。当使用Subsampling 抽样方法的时候就能避免参数κ的估计。具体步骤如下：

第一步，计算yt对μ和β回归的最小二乘估计残差：=yt--，t=1,2,…,T。

第二步，计算对ρ回归的最小二乘估计残差：

构造如下检验统计量：

为验证Subsampling 抽样方法的Ratio 检验有效性，下面给出原假设下的相合性。

定理3：当T→∞,b→∞时，满足b/T→0。若假设1和假设2同时成立，则对任意x>0，有。

在开发房地产之前，必须要考虑好供求关系，这对于房价、成本计算以及开发时间和房屋的数量等起到了重要的价值，也可以促进房地产行业的发展。可以促进城市的建设，在规划当中，还需要控制风险来让规划变得更具有可行性。

定理3：证明可参考文献[11]。

4 数值模拟

通过经验水平和经验势的模拟结果来说明上述基于Subsampling 抽样Ratio 检验趋势变点的合理性。以下是样本数据yt的产生过程：

考虑εt是一个AR（1）过程，εt=ρεt-1+ηt,ηt是独立同分布的厚尾序列。尾指数κ∊{1.1,1.2,…,1.9}。不失一般性，设置μ=0,β=0。考虑跳跃幅度∆∊{0,0.2,0.6,1}，自回归系数ρ∊{-0.9,-0.5,0,0.5,0.9}，变点位置v*∊{0.3,0.5,0.7}，置信水平α=5%，样本量T∊{300,500,1000}，进行3000次循环。

因经验水平都在5%的置信水平波动，所以经验水平的扭曲可以忽略。数值模拟结果（见表1 至表3）表明，首先，经验水平不依赖于自回归系数ρ，这和定理1 是一致的；其次，经验水平对尾指数的变化是敏感的；最后，随着T的增大，经验水平波动性减小。所以在原假设下，基于Subsampling 抽样的Ratio 检验能很好地控制经验水平。

表1 Subsampling抽样的Ratio检验的经验水平和经验势（T=300）

表2 Subsampling抽样的Ratio检验的经验水平和经验势（T=500）

表3 Subsampling抽样的Ratio检验的经验水平和经验势（T=1000）

Subsampling抽样的Ratio检验在备择假设下的经验势受到样本量、跳跃幅度、变点位置、自回归系数和尾指数的影响，纯模拟结果表明：

（1）随着样本容量T=300,500,1000 的增加，统计量的经验势随之增加。这与定理2 是一致的，即在存在趋势变点的情况下，样本量越大，统计量越发散。

（3）统计量在后端的经验势大于在前端的经验势，即变点在后端时更易检验。例如当T=300,∆=0.6,ρ=0.5,κ=1.7 时，对于v*=0.3,0.5,0.7，经验势分别是0.4805、0.8535和0.9420。

（4）在一阶自回归过程中，ρ≤0 的经验势大于ρ>0的经验势，这和定理2 是一致的。除ρ=-0.9 之外，其余自回归系数的经验势近似重合。例如当T=500,∆=0.6,v*=0.7,κ=1.7 时，对于ρ=-0.5，ρ=0 和ρ=0.5，经验势分别为0.9680、0.9640和0.9560。

（5）当∆=0.2,κ≤1.6 时，即使T很大，经验势也比较低，所以很难检验出趋势变点。但当κ>1.6 时，经验势就比较高。因趋势变点的发散速度为T3-2/κ，所以κ较大时有更快的发散速度。以上的数值模拟结论说明Subsampling抽样的Ratio统计量能够检验厚尾序列的趋势变点。

5 谷歌股票价格分析

为通过实际应用说明Subsampling 抽样的Ratio 统计量能够检验趋势变点，选取2016 年8 月19 日至2018 年1月18 日谷歌股票收盘价的356 次观察数据（见图1）进行实证。首先，根据Perron 和Zhu（2005）[9]提出的方法估计趋势变点=173，把整个样本序列分成两段[1,173] 和[1 74,356],修正后的序列定义为,t=1,…,356,,其 中，=783.4415,=0.4282，=0.3605；其次，使用贝叶斯信息准则，判定为AR(1)模型并计算临界值Ξb(0.05)=0.8406，其中，α=0.05，b=45；然后，用原始序列zt代替vt代入Ratio 统计量，得到Ξ=0.9047>0.8406，说明序列确实存在趋势变点；最后，由于序列若存在持久性变点，也会出现上述现象，因此应用Kim（2000）[14]提供的Ratio统计量检验此变点，并未发现持久性变点。所以，该序列存在趋势变点。

图1 Google股票收盘价

6 结束语

本文提出基于Subsampling 抽样的Ratio 统计量来检验厚尾AR(p)序列趋势变点。在原假设下推导出统计量的极限分布是列维过程的泛函，在备择假设下得到统计量的一致性。同时，Subsampling抽样对于厚尾AR(p)序列有比较精确的临界值。蒙特卡洛数值模拟结果表明该抽样的Ratio检验实现了较好的经验水平和经验势。最后，通过一组数据阐明了理论的可行性和有效性。总之，基于Subsampling 抽样的Ratio 检验是判断厚尾序列有趋势变点的有效工具。