Kaili HE(贺凯莉)Jianxun HE(何建勋))Zhenzhen LOU(娄珍珍)

School of Mathematics and Information Sciences，Guangzhou University,Guangzhou 510006，China E-mail: kailihe@e.gzhu.edu.cn; heji.anaun @gzhu.edu.cn; zhenzhenlou@e.gzhu.edu.cn

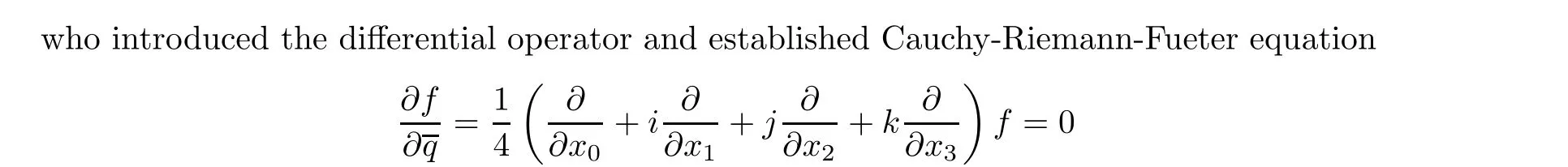
in 1935. A lot of significant conclusions have followed on from this, including Cauchy’s theorem[9]and Cauchy’s integral formula[10]. Nevertheless,the polynomials and series fail to be regular in the sense of Fueter. The other definition was proposed by Cullen[11]in 1965. He considered solutions of the equation

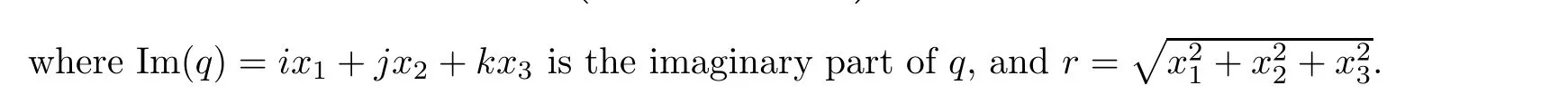
Let S={q ∈H: q2=-1}denote a 2-dimension sphere in the 3-dimension space of purely imaginary quaternions. Then H is regarded as a union of the complex planes LI=R+IR for I ∈S, where LIare isomorphic to C and intersect in the real axis. Two quaternions commute if and only if they belong to the same LI. Recently, Gentili and Struppa developed Cullen’s definition in [12, 13]. They claim that a function is Cullen-regular if its restriction on each complex plane is complex holomorphic. In other words, the function fIsatisfies

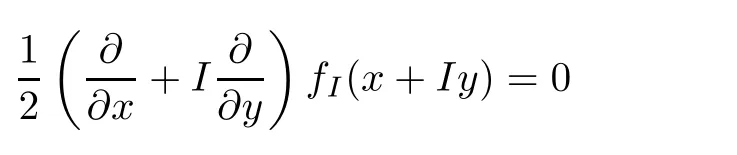
for x, y ∈R and for all I ∈S. If f and g are C-regular on Ω, then f +g is C-regular. By contrast, pointwise multiplication is not closed except for special cases. As an example, if f is slice preserving, then fg is C-regular on Ω [14].

The paper is organized as follows: in Section 2, we recall basic concepts and properties of a quaternion left Hilbert space. In Section 3, we extend the classical interpolation theorems of Riesz-Thorin with the maximum modulus principle from [14]. Section 4 describes the primary results of the first and second complex interpolation in Lp(C,H).

2 Preliminaries

The non-commutative algebra of quaternion H,as a special kind of Clifford algebra,consists of four real numbers and three imaginary units defined by

which follows

Every q ∈H can be expressed in Cayley-Dickson form

and has a quaternion conjugate

A quaternion left Hilbert space H has an inner product [18]

where f = f1+jf2, g = g1+jg2. The last of these inequalities is evident from the discrete form of Minkowski’s inequality. Moreover, Lp(R2,H) is a Banach space in a quaternion field.Specifically, L1(R2,H) is a Banach space of all quaternion valued functions f =f1+jf2on R2satisfying

L2(R2,H) is a left H-Hilbert space with the inner product

3 Interpolation of Operators on Lp(C,H)

There are two major elements of subsection 3.1. The first is to show Theorem 3.5. The trick of the proof here is to find a sequence of functions which are Cullen-regular in a symmetric slice domain. The second element, which is the main novelty of this paper, is Theorem 3.9; this is deduced from Theorem 3.5 and Proposition 3.8.

In Subsection 3.2, we conclude this section with two immediate consequences of Theorem 3.9.

3.1 The Riesz-Thorin interpolation theorem on Lp(C,H)

We first recall the modified versions of Cullen-regular functions of a quaternionic variable which come from [12-14]. Let Ω be a symmetric slice domain, let S = {q ∈H : q2= -1} be the sphere of purely imaginary unit quaternions, let ΩI= Ω ∩LIand LI= R+IR for I ∈S,and let fIdenote the restriction of f on ΩI. Definitions 3.1-3.3 and Lemma 3.4 are from [14].

Definition 3.1 Letting Ω be a domain in H,f : Ω →H is Cullen-regular if, for all I ∈S,its restriction fI: ΩI→H is complex holomorphic.

Definition 3.2 For all J ∈S with J ⊥I and every z = x + Iy, the function fIis holomorphic if and only if it is denoted by

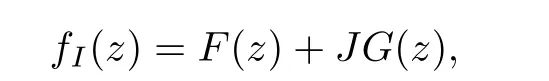
where F, G: ΩI→LIare complex-valued holomorphic functions of one complex variable.Definition 3.3 Ω is called a slice domain if, for all I ∈S, ΩI=Ω ∩LIis a domain of LI.Lemma 3.4 (Maximum modulus principle) Let Ω ⊆H be a symmetric slice domain and let f : Ω →H be C-regular. If ‖f‖Hhas a relative maximum at p ∈Ω, then f is constant.

To obtain the interpolation theorem, we give Hadamard’s three-lines theorem below. The foundational tool is Lemma 3.4.

Theorem 3.5 Suppose that Ω = {q ∈H | x0∈(0,1), x1, x2, x3∈R} is a symmetric slice domain. Let φ : Ω →H be a C-regular function in Ω, bounded and continuous on Ω.For any I ∈S, if there is ‖ φI(z)‖H≤k0on the line Re z = 0 and ‖ φI(z) ‖H≤k1on the line Re z =1, then for each 0 ≤θ ≤1, we have ‖φI(z)‖H≤k1-θ0kθ1on the line Re z =θ.

Proof Without loss of generality, we assume that I = i and J = j. It follows from Definition 3.2 that φi(z)=φ1(z)+jφ2(z) is holomorphic in the domain

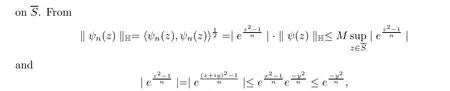
we obtain that ψn(x+iy) converges uniformly to 0 as | y |→∞. We can find yn> 0 such that ‖ ψn(z)‖H≤1 for all | y |≥yn, 0 ≤x ≤1. By Lemma 3.4 of the restriction function, we have ‖ψn(z)‖H≤1 on the rectangle {z =x+iy : 0 ≤x ≤1, -yn≤y ≤yn}. It follows that‖ψn(z)‖H≤1 on S for each n ∈N. As n →∞, we have thus proved the theorem. □

Remark 3.6 Thanks to the Splitting Lemma [14], we claim that φ1, φ2are complexvalued holomorphic functions,which implies that φiis holomorphic. In fact,for all J ∈S, J ⊥I,

We then have that

It follows that φ(ξ)∈Lpj(C,H)and ψ(ξ)∈Lq′j(C,H),and hence,T φ(ξ)∈Lqj(C,H), j =0, 1.Remark 1.8 in [14] implies that the slice derivatives φ＇(ξ), ψ＇(ξ) and (T φ)＇(ξ) are regular in 0 ＜Re ξ ＜1. Set

By Definition 3.7, we draw the conclusion that φ(ξ), which follows the Leibniz formula for slice derivatives, is C-regular on the open strip 0 ＜Re ξ ＜1, and is bounded and continuous on the closed strip 0 ≤Re ξ ≤1.

Next, we note that

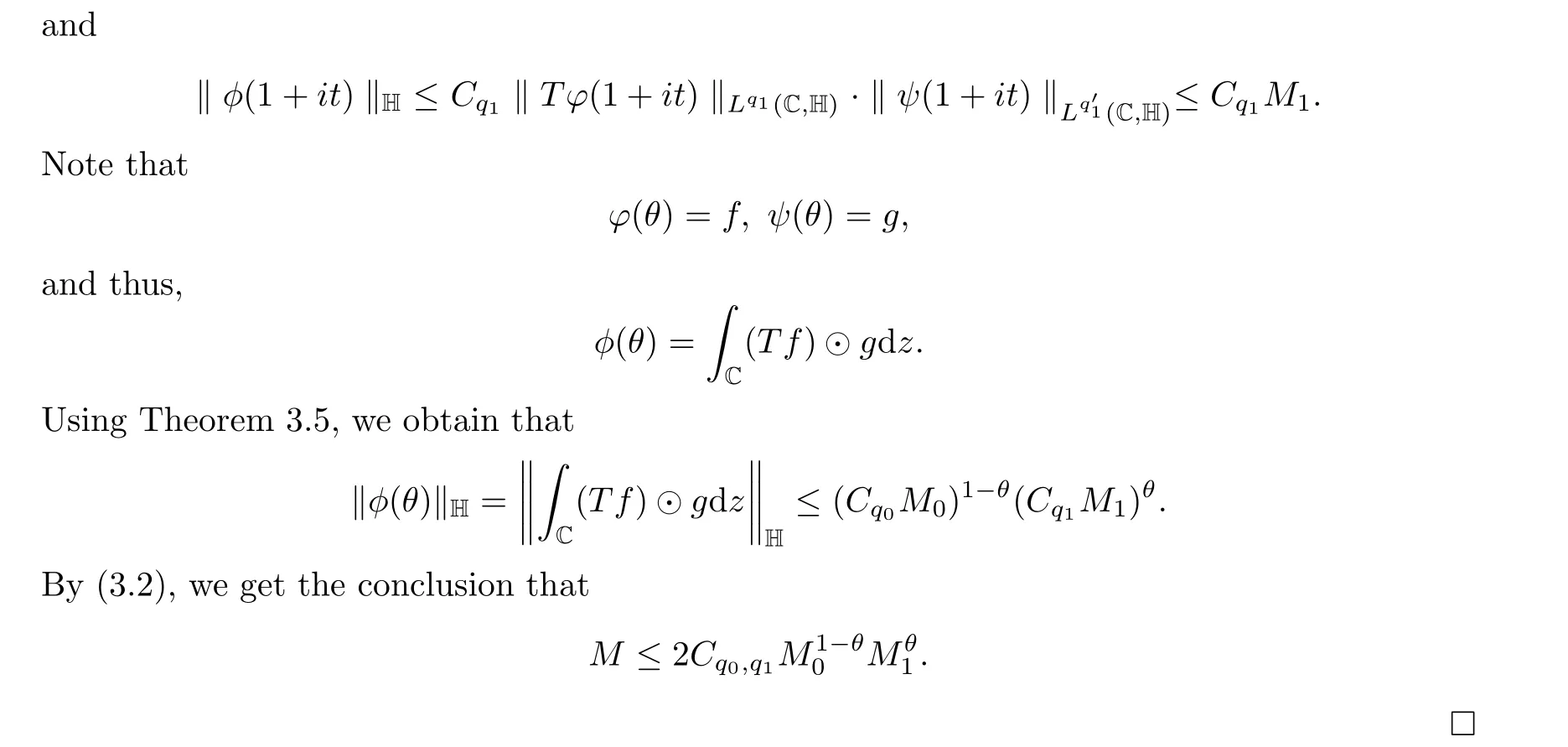
3.2 Corollaries of the Riesz-Thorin interpolation theorem

In order to obtain Corollary 3.13, we need the knowledge of QFT that is contained in[15, 18].

QFTs play a vital role in the representation of multidimensional (or quaternionic) signals.Due to the non-commutative property of multiplication of quaternions,there are different types of QFTs. In [15], it turns out that there exists a unitary form of the Plancherel formula, in spite of its different meanings.

This Lemma is a tool for proving the following corollary along the lines of the classical proofs in complex analysis:

In general,g ⊛f is not the same as f ⊛g. If both f and g are complex valued functions or if one of them is a real valued even function, then we obtain that f ⊛g =g ⊛f.

4 Interpolation of Lp Spaces

4.1 Two types of complex interpolation method

In this section, we investigate the complex interpolation of Lpin two ways. By Remark 3.6, the function f :S →H is holomorphic if we admit that f1, f2are complex analytic.

Definition 4.1 Letting (Lp0(C,H),Lp1(C,H)) be a Banach couple [5], the norm on Lp0(C,H) +Lp1(C,H) is defined by

If C =1, we say that Lp(C,H) and Lq(C,H) are exactly of exponent θ.

Next, we give definitions of the first complex interpolation spaces and their functions.

It is now obvious that the theorem holds. □

4.2 Properties and equivalence of the complex interpolation methods

We shall introduce the relation between the first and the second complex interpolations,including the equivalence theorem. For the first complex interpolation space, we have the following: