求解大型广义绝对值方程的Picard-SS迭代法
2023-01-03尹晓霞
尹晓霞,李 旭
(兰州理工大学理学院,甘肃 兰州 730050)
考虑求解大型广义绝对值方程 (GAVE)
Ax-B|x|=b,
(1)
其中:A,B∈n×n与b∈n都是给定的矩阵和向量,|x|=(|x1|,…,|xn|)T∈n表示对x的每个分量取绝对值。当B是单位矩阵时,GAVE 特殊化为绝对值方程 (AVE):
Ax-|x|=b。
(2)
许多科学计算和工程应用领域中的优化问题[1]都归结为求解GAVE(1),该方程的一个重要研究来源是如下的线性互补问题LCP(q,M)[2]:
对于给定的矩阵M∈n×n和向量q∈n,求一对实向量z,ω∈n使得
z≥0,ω=Mz+q≥0,zTω=0。
(3)
根据文献[3-5],线性互补问题 (3) 可转化为如下 GAVE:
(M+I)x-(M-I)|x|=q,
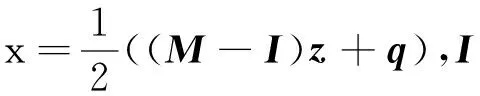
在理论分析方面,最早是由Mangasarian给出了GAVE(1)解存在的充分条件,随后一些学者改进和丰富了解的存在性理论[6-8]。在数值算法方面,除了早期的有限逐次线性化方法[9]、整数规划法[10]和符号一致算法[11],Mangasarian通过引入非线性项|x|的次梯度,提出了广义Newton(GN)迭代法。之后为了进一步提高计算效率,产生了一些改进GN的迭代法,如广义Traub迭代法[12]、修正GN迭代法[13]、松弛GN迭代法[14]等,但这些方法都有一个很大的缺陷,每一步迭代都需求解不同系数矩阵的线性系统,从而导致计算成本很高。
为了克服这一问题,针对GAVE(1),Rohn等[15]提出了非常高效的Picard迭代法:
Ax(k+1)=B|x(k)|+b,k=0,1,2,…,
(4)
其中:x(0)=A-1b是初始估值。
鉴于Picard迭代中的每一个线性系统的系数矩阵都是A,因此可以利用矩阵分裂方法高效求解这些子系统。Salkuyeh给出了一个很好的范例,并结合著名的Hermitian和反Hermitian分裂(HSS)迭代法[16],提出了求解AVE(2)的Picard-HSS迭代法[17]。收敛性分析表明Picard-HSS迭代法的收敛性与初值的选取无关,数值实验表明Picard-HSS迭代法比Picard迭代法和GN迭代法更高效。最近,Miao等学者利用单步HSS(SHSS)迭代法[18]提出了求解AVE(2)的Picard-SHSS迭代法[19]。
针对求解非Hermitian正定线性系统,Bai等[20]提出的Shift分裂(SS)迭代法是一种相较于HSS和SHSS迭代法更加高效的算法,尤其是针对条件数很大的情形。基于这一点,将Picard迭代法作为外迭代,对于每一步外迭代对应的线性系统,将SS迭代法作为内迭代求解器,建立求解GAVE(1)的Picard-SS迭代法,并且给出该方法的收敛性分析,最后通过数值算例检验Picard-SS 迭代法的可行性和高效性。
1 Picard-SS迭代法的建立
针对非Hermitian正定线性系统
Ax=b,
(5)
Bai等[20]利用A的Shift分裂(SS)
提出了如下求解线性系统(5)的Shift分裂(SS)迭代法:
算法1(SS迭代法)对于给定的任意初始向量x(0)∈n,l=0,1,2,…,利用下述迭代格式计算x(l+1)直到迭代序列n收敛:
(αI+A)x(l+1)=(αI-A)x(l)+2b,
(6)
式(6)中α为给定的正常数。
将SS迭代法运用到Picard迭代法的每一个子迭代线性系统(4),建立如下求解GAVE(1)的 Picard-SS迭代法。
算法2(Picard-SS迭代法)设A∈n×n是非Hermitian对称正定矩阵,B∈n×n。对于给定的任意初始估值x(0)∈n,k=0,1,2,…,利用迭代格式计算x(k+1)∈n直到迭代序列满足停止准则:
(1) 设x(k,0):=x(k);
(2) 对于l=0,1,2,…,lk-1,应用如下SS迭代法求解得到x(k,l+1):
(αI+A)x(k,l+1)=(αI-A)x(k,l)+2(B|xk|+b),
(7)
其中:α为给定的正常数;
(3) 令x(k+1):=x(k,lk)。
注1与HSS迭代法[16]相比,SS迭代法式(7)的优势在于单步迭代;与SHSS迭代法相比,SS迭代法式(7)的优势在于无条件收敛。因此Picard-SS迭代法在更短时间内得到迭代解,从而可以大大降低计算成本。
注2在算法2中,若取B为单位矩阵,则得到求解AVE(2)的Picard-SS迭代法。
2 收敛性分析
为了后续讨论方便,记
首先将Picard-SS迭代法的内迭代式(7)等价改写为以下形式:
x(k,l+1)=T(α)x(k,l)+G(α)(B|x(k)|+b),
(8)
这里
T(α)=M(α)-1N(α),G(α)=M(α)-1。
进一步可将式(8)改写为
x(k+1)=T(α)lkx(k)+
(9)
根据文献[21]中引理2.1,对于内迭代矩阵T(α)有如下引理:
引理1设A∈n×n是非Hermitian正定矩阵,记ρ(T(α))为T(α)的谱半径,则有
ρ(T(α))≤‖T(α)‖2≤
‖(αI+A)-1(αI-A)‖2<1。
接下来给出并证明Picard-SS迭代法的收敛性定理。
定理1设A∈n×n是非Hermitian正定矩阵,B∈n×n是非奇异矩阵。令η=‖A-1B‖2<1,则GAVE(1) 存在唯一解x*。对任意的x(0)∈n以及任意正整数序列设若
(10)
则由Picard-SS迭代法生成的迭代序列x(k)收敛于精确解x*。
证明为方便讨论,将GAVE等价改写为如下形式的AVE:
B-1Ax-|x|=B-1b。
根据条件η=‖A-1B‖2<1,由文献[4]中的命题4可得,以上方程有唯一解x*。
由于唯一解x*也满足不动点方程
(αI+A)x*=(αI-A)x*+2(B|x*|+b),
(11)
同样可将式(11)等价改写为
(12)
式(9)与式(12) 相减,得
x(k+1)-x*=T(α)lk(x(k)-x*)+
(13)
因为ρ(T(α))<1,有
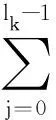
(I-T(α)lk)(I-M(α)-1N(α))-1M(α)-1=
(I-T(α)lk)A-1,
(14)
将式(14)代入式(13)得
x(k+1)-x*=T(α)lk(x(k)-x*)+
(I-T(α)lk)A-1B(|x(k)|-|x*|)=
T(α)lk[(x(k)-x*)-A-1B(|x(k)|-
|x*|)]+A-1B(|x(k)|-|x*|),
(15)
对式(15)两边同取2-范数,可得
‖x(k+1)-x*‖2≤(‖T(α)lk‖2(1+η)+
η)‖x(k)-x*‖2。
根据条件(10)有

容易得到以下的残量更新形式以方便实际计算。
算法3(Picard-SS迭代法的残量更新形式)设A∈n×n是非Hermitian对称正定矩阵,B∈n×n。对于给定的任意初始估值x(0)∈n,k=0,1,2,…,利用下述迭代格式计算x(k+1)∈n直到迭代序列满足停止准则:
(1) 设s(k,0):=0,b(k)=B|x(k)|+b-Ax(k);
(2) 对于l=0,1,2,…,lk-1,应用如下SS迭代法求解得到s(k,l+1):
(αI+A)s(k,l+1)=(αI-A)s(k,l)+b(k),
其中:α为给定的正常数;
(3) 令x(k+1):=x(k)+s(k,lk)。
3 数值实验
通过外迭代步数 (记作ITout)、内迭代步数 (记作ITint) 和CPU时间 (单位为秒,记作CPU)3个指标比较Picard-HSS和 Picard-SS迭代法求解GAVE (1) 的计算效率。由于SS迭代法是单步迭代,为了公平比较,我们将SS迭代法也写成两步迭代的格式计内迭代步数,数值实验实现平台:Matlab,Intel(R) Core(TM) i5 processor (2.20 GHz,4 GB RAM),在算法实现时,取初值x(0)=(1,0,1,0,…,1,0,…)T,外迭代停止标准为
内迭代停止标准为



为块三对角矩阵,
S=Tridiag(-1.5,4,-0.5)=

为三对角矩阵,n=m2且z*=(1.2,1.2,…,1.2,…)T是LCP(q,M)的唯一解。因此
x*=(-0.6,-0.6,…,-0.6,…)T
是GAVE(1)的精确解。
对于不同的规模n,表1和表2分别列出了当μ=4和μ=10时两种迭代法的数值结果,包括实验最优迭代参数、内外迭代步数以及CPU时间。
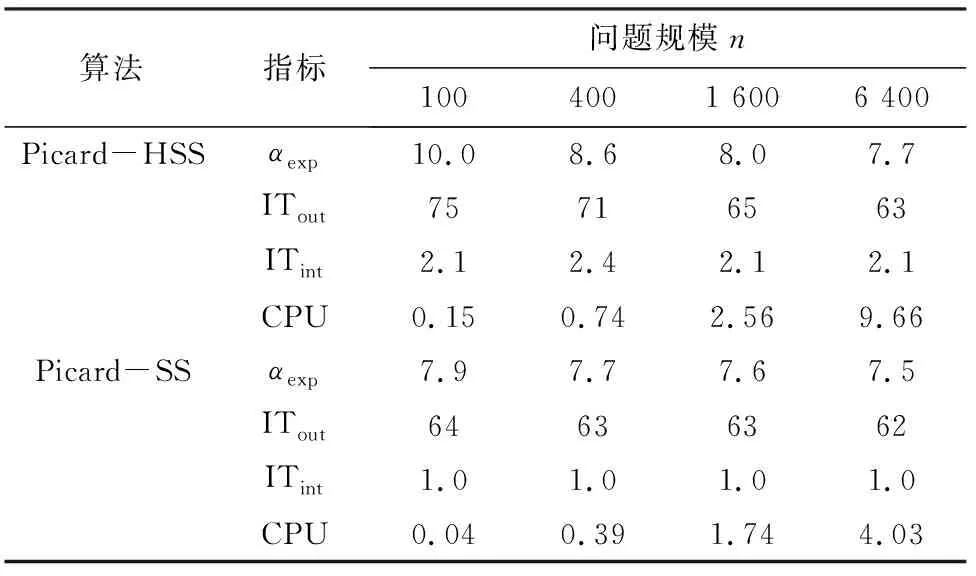
表1 μ=4的数值结果Table 1 Numerical results with μ=4

表2 μ=10的数值结果Table 2 Numerical results with μ=10
从表1和表2容易看出,随着问题规模n的增大,无论是内外迭代步数还是CPU时间,Picard-SS迭代法都要明显优于Picard-HSS迭代法。因此可知,Picard-SS迭代法是求解GAVE(1)的一种非常高效的方法。
4 结论
对于求解大规模广义绝对值方程,研究利用Picard内迭代线性系统的系数矩阵的Shift分裂(SS),提出了相比现存迭代法更加高效的Picard-SS迭代法,详细分析了该方法的收敛性,并且通过数值实验验证了其有效性和优越性。
