曹 辉 程守山 (江苏省常州市北郊高级中学 213032)

刘天程 (江苏省常州市正行中学 213017)

所谓深度学习是指教师借助一定的活动情景带领学生超越表层的知识符号学习，进入知识内在的逻辑形式和意义领域，挖掘知识内涵的丰富价值，完整地实现知识教学对学生的发展价值.本文以教学追问为活动方式，“三维一体”为设计思路，引导学生深度学习[1].在解析几何的教学过程中，教师往往以试题训练为“点”、以掌握通法通解为“面”来达到教学目标.实际上，通法通解是连接知识方法的“线”，对知识方法起到桥梁作用，“面”则是知识体系形成的关键，最后提炼思想方法，形成跨体系、跨学科、跨领域的“体”，而“体”即是能力，是知识方法的核心规律对学生理性思维和关键能力的培养.

本文以一道椭圆中的定值定点问题为例，通过问题引领、深化和追问，将知识和技能由“点”到“面”深入到思维的层面，进一步构建椭圆中一类定值定点问题的知识体系，从而实现“数学本质”和“知识交汇”的“体”，提升高三一轮复习课的质量.

1 “点”到为“指”

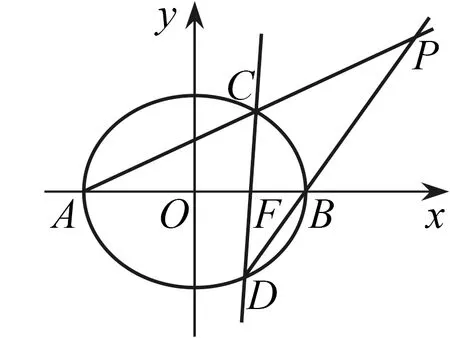
图1

·分析问题

点评以一道典型的定点问题为方向指引，抛砖引玉，打开学生思维的窗口.

·“点”到不止

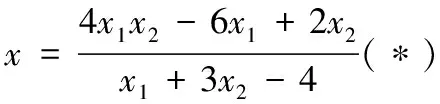
问题1 (*)式不能直接运用韦达定理，能否转化为单变量整体可约分？

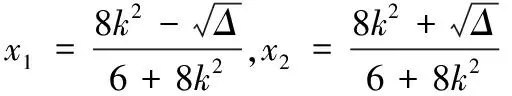
点评由于(*)式不能直接运用韦达定理，导致不少学生找不到解决问题的方法.实际上，韦达定理可利用求根公式得到，所以将求根公式代入(*)式，即将问题转化为单变量可约分为定值的问题.

问题2 你能根据特殊情况或对称性猜出答案吗？猜出答案后如何证明(*)式为定值？

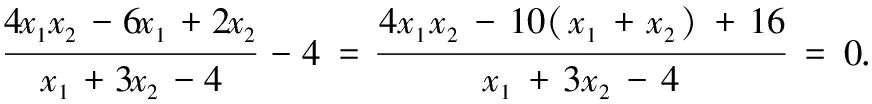
点评“先猜后证”是解析几何中常用的思想方法，学生可以根据斜率不存在和对称性判断出交点在x=4上，然后通过作差利用韦达定理证明猜想.

问题3 (*)式能否转化为双变量整体可约分问题？

点评以问题中的“单变量”和“双变量”引导学生思考，让学生进一步体会定值问题的单变量和多变量的整体可约分的思想方法.学生较易接受单变量可约分问题，对于双变量可约分问题则较为陌生，该解法进一步加深了学生对定值问题的理解.以上方法难度较大，可操作性不强，大部分学生会在(*)式的处理上遇到困难.

本题容易认为核心规律是(*)式处理的思想方法.实际上，题目中隐含着一类“定”的关系，如kACkBC,kBCkBD为定值，那么斜率之间的关系是否对解决该问题有帮助？能否通过问题设计、知识迁移得出一般结论和方法，从而达到掌握核心规律的目标？以该例题为“点”，通过问题设计，使问题问问相连，使各点环环相连，让学生进一步探究该图形中存在的“动”和“定”的问题.

2 “点”动成线

问题1 直线BC和直线BD的斜率乘积是否为定值？

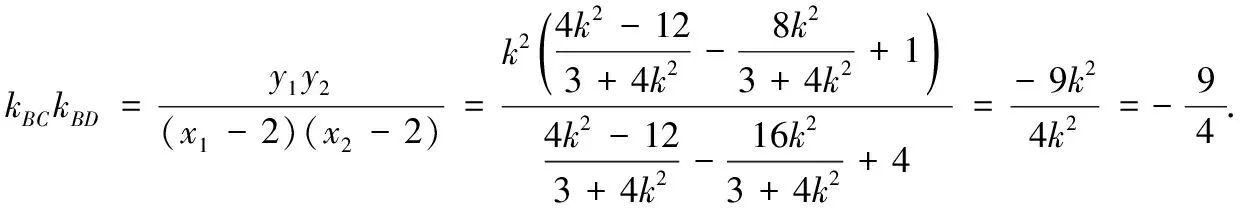
问题2 直线AC和直线BC的斜率乘积是否为定值？

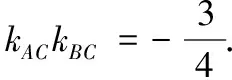
问题4 根据上述问题，能否用设AC斜率的做法求交点？

解得x=4.

3 线线交错

where only Ron and Roff appear, making clear their importance for this calculation. This happens despite QF has been defined in terms of NMR and NRS. Furthermore, expression(10) simplifies to whenever Roff Ron.

设计意图通过问题深化，学生将知识、方法过渡到一般性的思维策略，如图2.

图2

4 “线”动成“面”

下面通过条件和结论的互换，进一步对问题追问.对于问题深化中问题1的追问：

追问1 若已知直线BC和直线BD的斜率乘积为定值，直线CD是否过定点？

(备注：可以用直线方程和椭圆联立，借助韦达定理解决，此处不再赘述，可见文[4])

(备注：考虑到联立的复杂性，建议用齐次化联立解决问题，此处不再赘述)

对于问题深化中问题2的追问：

追问 若kAC=λkBD(λ为定值)，直线CD是否一定过定点？

对于问题深化中问题3的追问：

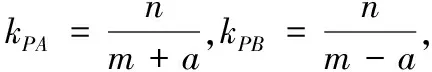
设计意图学生不可能一次性把握数学活动的本质，故需要教师进一步思考和研究知识方法的本质.追问的设计旨在从“点”到“面”的进一步升华，进一步培养学生的理性思维和关键能力，让学生经历发现问题→解决问题→再发现问题→再解决问题的过程，进一步掌握知识的“源”与“流”.针对上述问题的提出和解决，2021年和2020年新高考全国I卷(22)以及2020年全国I卷(20)解析几何题目便可迎刃而解.

5 “面”动成“体”

在这一过程中让学生体会“形缺数时少直观，数缺形时难入微”的数形结合思想，在整体消元中让学生感受函数与方程思想，这两大数学思想贯穿着初等数学的始末.将两大思想牵引到其他知识块，如：立体几何、三角函数等，学生遇到陌生问题就不会因恐惧而束手无策.如今年新高考I卷的第8题、第21题等.从一题多法到通法，提炼思想方法，实现一法解多题.借助有效追问实现了点动成线，线动成面，面动成体的生态循环，使学生实现深度学习.

6 教学建议

(1)批判性思维的培养

本文以例题中求交点的横坐标是定值的问题为“点”，通过问题引领，从新的角度进一步剖析问题，即发现kBD=kAC，将题目中以寻找变化过程中的不变关系为“点”发散，猜想、归纳、证明一般性结论为“线”，最后以追问的方式，从逆命题和知识方法联系的角度逐层深化椭圆中的定值定点问题形成“面”.追问的设计可以培养学生的批判性思维，即当一个命题成立时，培养学生自觉地思考其逆命题是否成立、是否可以探究出并判断其他相关命题是否成立.

(2)教学追问的注意点

·追问目标要明确

高中生的智力发展得已经较为成熟，因此，教师在设计问题时要结合学生对知识的理解水平提出有回答意义的问题，同时还要有明确的提问方向，提出的问题要清晰明了，能让学生明确所提问的目标[2].

·追问要及时

随着课堂教学方式的不断进步，教师逐渐转变了教学方法，明白了追问的重要性，在课堂中逐渐增加了设计问题和让学生回答问题的环节.但在这一环节教师需要注意的是，设计的问题一定要紧紧围绕自己所讲解的知识点，最好能够结合以前学习过的知识让学生自发地与新知识进行对比并总结.同时教师还需注意的是，所提问题一定要及时，合理安排问题并确定问题应当提在哪里.课堂动态的把握、课堂的生成是新老教师的最大区别.

·追问要主客体互动

核心素养下的高中数学课堂一定是以讨论为主的教学相长的学习共同体，能充分发挥学生主体性的课堂.学生在进行新知识的学习时一定或多或少地存在问题，因此，教师要引导学生对自己无法理解或掌握不好的地方踊跃提问.

·追问要有度

一节课不是在任何时候都有必要追问，尤其数学课堂，本身容量大、时间紧，在预设追问上更要精细.所以以课前预设的追问为主，课堂生成的追问为辅，如果不影响教学目标，有更好的生成追问突破重难点、拓宽学生思维，那么这样的生成追问是必要的.

高三教学不是知识方法的堆积，也不是教师一言堂式的讲解，它强调的是理智和情感的互动、思维方式的深层追问和高阶思维的培养.同时，教学中要求教师投入更多的精力去理解知识方法的广度、深度、关联度，主动构建知识方法的系统，通过问题设计将知识和方法深入到思维的层面，提升学生的思维品质，达到培养学生数学学科素养的目的.