马林涛,孙 婷,黄荣里

(广西师范大学 数学与统计学院,广西 桂林 541006)

0 引言

本文研究一维抛物型方程第二边值问题的长时间渐近行为,其极限解与平移孤立子密切相关.演化方程的特殊解通常又称为孤立子,孤立子在演化过程中保持其形状.例如,在平均曲率流中有两类非常重要的孤立子,它们分别是自收缩解和自膨胀解以及通过平移演化而来的平移解.孤立子是抛物方程解的一个有趣的例子,它们是精确的解,它们的演化是完全已知的,通常可以通过求解相应的椭圆方程得到.鉴于此，我们考虑利用经典傅里叶级数的性质证明一类带热源的热传导方程第二边值问题的解的极限必然是一类平移孤立子,而且这类平移孤立子可以通过求解一类二阶微分方程得到.关于抛物型方程第二边值问题的渐近行为,已有的研究结果如下.

设Ω是Rn中具有光滑边界的有界区域,S为Sn的连通开集,其中Sn为n阶实对称矩阵的集合.给定函数u0：Ω→R，文献[1]考虑了具有第二边界条件的非线性抛物型方程

(1)

由方程(1)可以得到一类特殊的方程

及其解

满足

本文考虑一维抛物型方程第二边值问题

(2)

其中f(x,t)表示物体内部热源强度,a,b为两个常数,u0(x)是区间[0,1]上的光滑函数.在物理意义上该模型描述了一种金属棒在区间[0,1]上与两个端点0,1进行热交换的热传导问题.我们的主要目的是分析当f(x,t)≠0时,方程的解的渐近性质.

接下来在给出建立本文主要结论需要用到的预备知识后,再分析一维抛物型方程第二边值问题(2)在一定假设下解的渐近性态.根据经典傅里叶级数的性质我们发现一维带热源的抛物型方程第二边值问题的解在长时间的渐近行为下其极限必然是一类平移孤粒子.

1 预备知识

命题1.1(Fourier级数逐项微分定理)[2]设f(x)在[0,1]上连续,

f(0)=f(1),且除有限个点外f(x)可导.进一步假设f'(x)在[0,1]上可积或绝对可积(注意：f'(x)在有限个点可能无定义,但这并不影响其可积性),则f'(x)的Fourier级数可由f(x)的Fourier级数逐项微分得到,即

命题1.2(L'Hospital法则)[3]设函数f(x)与g(x)在(a,a+d]上可导(d是某个正常数),且g'(x)≠0.若此时有

或

成立.

2 主要结论

定理2.1设

(1) ∀x∈[0,1],f(x,t)→f0(x)(t→∞);

(2)f(x,t)在[0,1]×(0,∞)上连续,

则方程(2)的解u(x,t)满足

(3)

注2.1定理中f(x,t)需满足当t→∞时f(x,t)收敛于f0(x),且f(x,t)要为区域[0,1]×(0,∞)上的连续函数这一条件说明在满足上述条件的情况下,求积分与求极限可交换.但很遗憾满足连续这个条件的函数不多,故若能将这一条件放宽将是一个更有趣的问题.

定理2.2设

(1) ∀x∈[0,1],f(x,t)→f0(x)(t→∞);

(3)f(x,t)在[0,1]×(0,∞)上连续,

则方程(2)的解u(x,t)满足

3 定理的证明

定理2.1的证明根据经典线性偏微分方程理论中的叠加原理[4]及分离变量法[5],我们可得方程(2)的解u(x,t)的表达式如下：

其中

λn=nπ,

到此我们令

即有

接下来,记

(4)

由w(x)的定义及Fourier级数逐项微分定理[2]我们对(4)逐项求导可得

(5)

(6)

为了下面求解方便,将f0(x)+(b-a)傅里叶余弦展开得

(7)

再将(7)移项后带入(6)得

最后,将x=0,x=1分别代入方程(5)中得

w'(0)=a,w'(1)=b.

综上,可以得到方程组

(8)

由定理2.1可知当t→∞时,

故为证明定理2.2成立,仅需证当t→∞时,

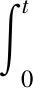
即当t→∞时,

定理2.2的证明由条件(1)可知

故有

4 结束语

本文发现一维带热源的抛物型方程第二边值问题的解在长时间的渐近行为下其极限必然是一类平移孤立子.对一般的非线性抛物方程(1),如果算子F与时间t有关,那么该收敛性定理是否成立依然有待进一步研究.