刘诗嘉，李 琦，高一天，黄在堂

(南宁师范大学 数学与统计学院,广西 南宁 530100)

1 引言

植物和传粉者之间的相互作用是非常有趣和复杂的.这两个物种相互依赖，植物为传粉者提供食物，传粉者在获得食物(花粉、花蜜或两者兼而有之)的过程中为植物传粉.这种互动关系通常被归类为互惠互利关系.植物物种依靠传粉者获得繁殖成功，从而物种生存下来，而传粉者依靠植物获得食物资源.在极端情况下，两个物种都离不开另一个物种[1，2].

1976年， May[3，4]首先提出了一个植物传粉者模型，模拟了植物与其传粉者之间具有义务关系的相互作用.为了避免模型出现不切实际的种群增长，May将植物从传粉者身上获得的益处和产生的曲线等位线的饱和效应结合起来.他最后解释了为什么在温带生态系统中，义务共生不如在热带生态系统中突出.由于食草动物以花为食，因而降低了许多植物物种的繁殖成功率，这一点已经得到了充分的证明.成功率的降低主要是由于配子的丢失.然而，花被食草动物攻击可能会通过减少传粉者的服务间接地阻碍植物的繁殖[5-8].因为传粉者对花的形态变化有反应.当食草动物攻击花朵时，造成的破坏会降低每朵花的广告属性，减少每次展示的花朵数量，降低传粉者的奖励.传粉者对植物的访问次数减少可能会导致植物繁殖成功率降低.Jang[9]以植物传粉者模型为基础，将一种食草动物物种引入该系统.具体来说，他将生物学观察纳入模型，并提出了食草动物植物传粉者模型.此后，Sánchez-Garduo等人[10-15]讨论食草动物植物传粉者模型的动力学.

最近(2019年)，Castellanos[16]提出了一个非线性食草动物植物传粉者数学模型，用于描述三个同质种群：两个共生种群，第三个种群早于两者的某一个.该模型即食草动物-传粉昆虫-植物模型

(1.1)

其中g∈C1[0,∞],g(0)=1,g′(z)≤0,g(z)>0,∀z≥0,且S,f,h分别表示

其中，x,y,z分别表示传粉昆虫、植物和食草动物在t时刻的种群密度.k1为每次授粉的效率常数，μ为传粉昆虫每次访问植物获得的能量奖励，α为植物死亡率.k表示传粉昆虫的多样性水平即传粉昆虫对于植物的专一性，当k=0时，没有植物，从而传粉昆虫不能生存；当k远大于0 时，授粉昆虫的数量基本没有变化.φ为一个与采蜜速度成反比的常数，k2是能量转化常数.b为密度相关调节常数，m1为食草动物最大摄食率，m2为食草动物最大出生率，a,c为与食草动物摄食量有关的参数.β为食草动物死亡率，与种群密度无关.g(z)表示传粉昆虫访问率的减少量，与食草动物的种群密度有关.

由于自然界中的种群系统不可避免地遭受突然的环境干扰，如火山爆发、海啸、台风、地震等[17-20]，因此，在种群模型中引入爆噪声或泊松噪声来描述这种连续或不连续系统是很自然的[21-25].但目前很多种群系统都是确定性的，它们的演化完全由初始数据决定，这显然与自然界的现象不一致.在对确定性食草动物植物传粉者模型研究过程中，人们容易忽略自然界中由于光照、水分、空气、温度、湿度等环境因素对物种生存的影响，这些因素都可能导致食草动物植物传粉者模型中种群密度的随机波动.因此，在食草动物植物传粉者模型中引入适当的环境噪声因素，能使对食草动物植物传粉者模型的研究更加贴近实际.因此，本文考虑具有非中心泊松噪声的随机食草动物植物传粉者模型

(1.2)

其中σi(i=1,2,3)是噪声强度，γi(t,u),δi(t,u)(i=1,2,3)是正的连续有界函数.ωi(t)(i=1,2,3)是相互独立的标准一维维纳过程，Ni(dt,du)(i=1,2,3)是相互独立的泊松过程，且泊松过程与维纳过程相互独立.设νi(A)(i=1,2)是博雷尔集A在上的有限测度.令E[Ni(t,A)]=tνi(A)(i=1,2)，则用S,f,h分别表示

2 正解存在唯一性

令概率空间为(Ω,F,P),ωi(i=1,2,3,t≥0)是在概率空间上相互独立的一维标准维纳过程.在概率空间(Ω,F,P)上定义相互独立的且与维纳过程相互独立的泊松过程Ni(dt,du)(i=1,2,3).

假设H1对于γi(t,u),δi(t,u),σi(t)(i=1,2,3),a(t),b(t),c(t),k(t),k1(t),k2(t),m1(t),m2(t),α(t),β(t),μ(t),φ(t)均为连续有界的关于t的函数，且这些函数的下确界均大于0.

假设H2ln(1+γi(t,u)),ln(1+δi(t,u))(i=1,2,3)是有界的,νi()<∞,i=1,2.

(2.1)

P{τ∞≤T}>,

则存在整数n1≥n0使得

P{τn≤T}>, ∀n≥n1.

(2.2)

在假设H1和假设H2成立条件下，由式(2.1)可以得到

(2.3)

V(x,y,z)=q1(x-1-lnx)+q2(y-1-lny)+q3(z-1-lnz).

运用伊藤公式，可以得到

dV(x(t),y(t),z(t))=LV(x(t),y(t),z(t))dt+q1σ1(t)(x(t)-1)dω1(t)+

q2σ2(t)(y(t)-1)dω2(t)+q3σ3(t)(z(t)-1)dω3(t)+

(2.4)

其中

(μ(t)φ(t)y(t)+1)-1[q1k2(t)μ(t)y(t)(x(t)-1)+

y(t))-1[q3m2(t)y(t)(z(t)-1)-q2m1(t)z(t)(y(t)-1)]+

(2.5)

对式(2.5)进行整理，可得

LV(t,x,y,z)=ζ1(t,x)+ζ2(t,y)+ψ1(t,x,y)+ψ2(t,z,y),x>0,y>0,z>0,

(2.6)

其中

q2k1(t)μ(t)g(z)xy-q2a(t)α(t)y-q3m2(t)y+q2k1(t)a(t)μ(t)g(z)x},

[-(q2m1(t)-q3m2(t))μ(t)φ(t)zy2+q2m1(t)μ(t)φ(t)zy-

(q2m1(t)-q3m2(t))zy+q2m1(t)z]-q3β(t)z.

根据假设H1和假设H2有，存在一个常数L1(q1,q2,q3)>0，使得以下不等式成立：

(2.7)

同理，根据假设H1和假设H2有，存在一个常数L2(q1,q2,q3)>0，使得

(q1k2sup+q2k1supgsup(z))asupμsupxy]≤L2(q1,q2,q3).

(2.8)

(q3m2sup-q2m1inf)zy+q2m1supμsupφsupzy+q2m1supz]≤

(2.9)

根据式(2.5)～(2.9)，可得到

LV(x(t),y(t),z(t))≤L(q1,q2,q3)+3C1+3C2,

(2.10)

其中

L(q1,q2,q3)=L1(q1,q2,q3)+L2(q1,q2,q3)+L3(q2,q3),

根据式(2.4)和(2.10)，可获得

V(x(τn∧T),y(τn∧T),z(τn∧T))≤V(x(0),y(0),z(0))+L(q1,q2,q3)(T∧τn)+

(2.11)

对式子(2.11)两边取期望，有

E[V(x(τn∧T),y(τn∧T),z(τn∧T))]≤

V(x(0),y(0),z(0))+L(q1,q2,q3)T.

(2.12)

从而，根据式(2.12)，可以得到

(2.13)

∞>V(x(0),y(0),z(0))+L(q1,q2,q3)T=∞.

因此τ∞=∞几乎处处成立.

3 灭绝性

本节主要讨论具有非中心泊松噪声的随机草食动物植物传粉者模型(1.2)的灭绝性.

引理3.1若假设H1和H2成立，则植物种群数量y(t)满足

证明根据伊藤公式，可以得到

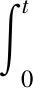
(3.1)

其中

由鞅不等式，对于任意的T>0,0<κ≤1,η>0，有

其中

令T=jτ,j∈,τ>0,κ=e-jτ,η=θejτlnj,θ>1，则有

即

根据不等式yr≤1+r(y-1),∀y≥0,0≤r≤1，可以得到

(3.2)

(3.3)

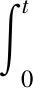
(3.4)

由定理2.1的证明可知，对于任意的x,y>0，存在一个独立于j,s,x,y的常数L>0，使得

由(3.4)可以得到，对于任意的(j-1)τ≤t≤jτ,k≥k0(ω),有

因此

若θ↓1,τ↓0，则可以得到

从而有

引理3.1证明完毕.

引理3.2若假设H1和H2成立，则食草动物种群数量z(t)满足

证明由伊藤公式，可以得到

其中

类似于引理3.1的证明方法，由鞅不等式可得，对于任意的T>0,0<κ≤1,η>0，有

其中

令T=jτ,j∈,τ>0,κ=e-jτ,η=θejτlnj,θ>1，则有

对于足够大的j≥j0(ω),0≤t≤jτ，根据Borel-Cantelli引理可以得到

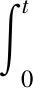
(3.5)

对于任意的(j-1)τ≤t≤jτ,k≥k0(ω),由(3.5)可以得到

因此

若θ↓1,τ↓0，则可以得到

故有

引理3.2证明完毕.

引理3.3若假设H1和假设H2成立，则传粉昆虫种群密度x(t)满足

证明由伊藤公式，可以得到

其中

类似于引理3.1的证明方法，可以得到

令T=jτ,j∈,τ>0,κ=e-jτ,η=θejτlnj,θ>1，则有

对于足够大的j≥j0(ω),0≤t≤jτ,根据Borel-Cantelli引理可以得到

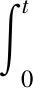
(3.6)

由(3.6)可以得到，对于任意的(j-1)τ≤t≤jτ,k≥k0(ω)，有

因此

若θ↓1,τ↓0，则可以得到

因而有

引理3.3证明完毕.

其中

证明由伊藤公式，可得

(3.7)

其中

由式(3.7)，可得

(3.8)

即

(3.9)

对(3.9)两边从t0到t进行积分，得到

从而

所以

由于ε>0，且x(t)>0 a.s.,故有

定理3.4证明完毕.

其中

证明由伊藤公式，可得

(3.10)

其中鞅为

且

由局部鞅的强大数定律[22]，可知

由于y(t)>0，a.s.，因此

定理3.5证明完毕.

其中

证明运用伊藤公式，可得

[k1(t)μ(t)x(t)-α(t)+D2(t)]dt+dMy(t),

(3.11)

其中

由局部鞅的强大数定律，可知

由于y(t)>0，a.s.,因此

定理3.6证明完毕.

其中

证明根据伊藤公式，可得

(3.12)

其中

由局部鞅的强大数定律可知

由于z(t)>0，a.s.,因此

定理3.7证明完毕.

4 持久性

本节主要讨论具有非中心泊松噪声的随机草食动物植物传粉者模型(1.2)的持久性.

引理4.1若假设H3和假设H4成立，令p>0，则有：

(1) 对于任意的初值x0>0，传粉昆虫的种群密度的p阶矩满足

其中K1(p)>0且与初值x0无关.

(2) 对于任意的初值y0>0，植物的种群密度的p阶矩满足

(4.1)

其中K2(p)>0且与初值y0无关.

(3) 对于任意的初值z0>0，食草动物的种群密度的期望满足

(4.2)

其中K3>0且与初值z0无关.

证明(1) 根据定理2.1的停止时间τn的定义，对过程V(t,y(t))=etxp(t),p>0，运用伊藤公式，可以得到

(4.3)

若假设H1和H2成立，则存在一个常数K1(p)>0，使得下式成立：

(4.4)

由(4.3)和(4.4)，对(4.3)取期望，可以得到

E[V(t∧τn,x(t∧τn))]≤xp(0)+K1(p)E[et∧τn]≤xp(0)+K1(p)et.

令n→∞,则有估计

etE[xp(t)]≤xp(0)+K1(p)et,

即

(2) 与(1)同理，对于式(4.1)，对过程V(t,y(t))=etyp(t),p>0，运用伊藤公式，可以得到

p[k1(s)x(s)f(y(s))g(z(s))-m1(s)z(s)h(y(s))-α(s)]+

(4.5)

若假设H1和H2成立，则存在一个常数K2(p)>0，使得下式成立：

esyp(s){1+p[k1(s)x(s)f(y(s))g(z(s))-m1(s)z(s)h(y(s))-α(s)]+

(4.6)

由(4.5)和(4.6)，对(4.5)取期望，可以得到

E[V(t∧τn,y(t∧τn))]≤yp(0)+K1(p)E[et∧τn]≤yp(0)+K2(p)et.

令n→∞，则有估计

etE[yp(t)]≤yp(0)+K2(p)et.

即

(3) 对于(4.2)，对过程

U(t,(x(t),y(t),z(t)))=et[q1x(t)+q2y(t)+q3z(t)],qi>0,i=1,2,3,

运用伊藤公式可以得到

dU(t,(x(t),y(t),z(t)))=et{q1x(t)+q2y(t)+q3z(t)+

q1[k2(t)x(t)y(t)f(y(t))+x(t)S(x(t))]+q2[k1(t)x(t)y(t)f(y(t))g(z(t))-

y(t)m1(t)z(t)h(y(t))-α(t)y(t)]+q3[m2(t)z(t)y(t)h(y(t))-β(t)z(t)]+

et[q1σ1(t)x(t)dω1(t)+q2σ2(t)y(t)dω2(t)+q3σ3(t)z(t)dω3(t)]+

对于函数

f1(x)+f2(x,y)+f3(z,y),

(4.7)

其中

f(t,x,y,z)≤L.

(4.8)

由(4.7)和(4.8)，对(4.7)取期望，可以得到

E[U(t∧τn,x(t∧τn),y(t∧τn),z(t∧τn))]≤

令n→∞，则有估计

于是

引理4.1证明完毕.

引理4.2若D3inf>βsup-m2inf，即f3inf>0,f3(t)=m2(t)-β(t)+D3(t),则对任意的初值z0>0，食草动物的种群密度z(t)满足

其中

(4.9)

当0<θ<1时，根据(4.9)和伊藤公式，得到

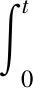
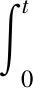
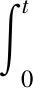
(4.10)

在假设H1和H2下，根据不等式(x+y)θ≤xθ+θxθ-1y,0<θ<1,x,y>0，知存在常数|K1(θ)|<∞,|K2(θ)|<∞，使得(4.9)中的Q(t)满足

K1(θ)U(t)+K2(θ)=-K0(θ)U2(t)+K1(θ)U(t)+K2(θ).

(4.11)

由于

根据条件f3inf>0，当0<θ<1足够小时，有

由式(4.10)和(4.11)，可以得到

d[(1+U(t))θ]≤θ(1+U(t))θ-2[-K0(θ)U2(t)+K1(θ)U(t)+K2(θ)]dt-

(4.12)

根据(4.12)和运用伊藤公式，可以得到

d[eλt(1+U(t))θ]=λeλt(1+U(t))θdt+eλtd[(1+U(t))θ]≤

(4.13)

(4.14)

根据定理2.1的停止时间τn的定义、式(4.13)和(4.14)，可得期望

令n→∞，则有

(4.15)

由(4.15)，可以得到

引理得证.

证明由引理4.1，可以得到估计

(4.16)

根据(4.16)，可以得到

这意味着动力系统有长期性行为.

定理4.4如果引理4.2条件成立，则对任意初值z0>0，食草动物种群密度z(t)拥有持久性.

证明根据引理4.1，有下式成立

即

根据引理4.2，可以得到

即

定理4.4证明完毕.

定理4.5如果定理3.6条件成立，且D2inf-αsup>0，则对任意初值y0>0，植物种群密度y(t)拥有持久性，其中

证明根据引理4.1，可以得到

即

同引理4.2证法，在假设H1和假设H2成立的条件下，根据不等式(x+y)θ≤xθ+θxθ-1y,0<θ<1,x,y>0，和z(t)=0，a.s.，知存在常数|K1(θ)|<∞,|K2(θ)|<∞，使Q(t)满足

K1(θ)U(t)+K2(θ)=-K0(θ)U2(t)+K1(θ)U(t)+K2(θ).

故有

即

定理4.5证明完毕.

其中

证明若定理不为真，则P{x*=0}>0.由(3.10)，可获得

(4.17)

其中

因此

由引理3.3可知

与已知矛盾，故定理4.6为真.

其中

证明若定理不为真，则P{z*=0}>0.由(3.12)，可获得

(4.18)

其中

因此

由引理3.2可知

与已知矛盾，故定理4.7为真.

其中

证明若定理不为真，则P{y*=0}>0.由(3.18)，可得到

(4.19)

其中

因此

由引理3.1可知

与已知矛盾，故定理4.8为真.