Yong Zhang, Yanwei Ren,2 and Huanhe Dong,*

1 College of Mathematics and Systems Science,Shandong University of Science and Technology,Qingdao 266590, China

2 College of Economics and Management, Shandong University of Science and Technology, Qingdao 266590, China

Abstract In this paper,based on the robust inverse scattering method,we construct two kinds of solutions to the focusing modified Korteweg–de Vries equation.One is the classical soliton solution under the zero background condition and the other one is given through the nonzero background.Especially, for the nonzero background case, we choose a special spectral parameter such that the nonzero background solution is changed into the rational travelling waves.Finally, we also give a simple analysis of the soliton as the time t is large,then we give the comparison between the exact solution and the asymptotic solution.

Keywords: robust inverse scattering method, modified Korteweg–de Vries equation, soliton solution, rational travelling waves, asymptotic analysis

1.Introduction

In this paper,we consider the complex modified Korteweg–de Vries (mKdV) equation

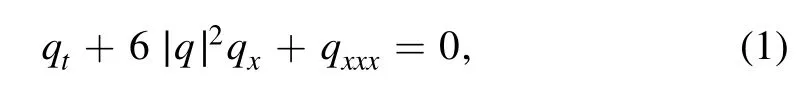
which is a well-known integrable equation admitting the following Lax pair

where

The compatibility condition about the Lax pair (2) generates the mKdV equation(1).In this paper,we would like to derive two kinds of higher order solutions to mKdV equation (1) via the robust inverse scattering method, one is the zero background and the other one is the nonzero constant background.In the terminology of inverse scattering methods[1–4],N-soliton solutions are constructed under the reflectionless case basing on that the scattering dataa(λ)hasNdifferent simple zeros,but the higher order solitons are different,it refers that the scattering dataa(λ)has multiple zeros.As a result,the velocity and the amplitude of N-soliton solutions are different unless the corresponding spectral parameters have some constraints, while the higher order solitons have the same velocity and amplitude due to sharing the same spectral parameter.

In 2017,Peter Miller and Deniz Bilman put forward to the robust inverse scattering method to construct the higher order rogue waves of NLS equation successfully, which makes it possible to derive the rogue wave under the framework of inverse scattering method [5].More importantly, they also established the Riemann–Hilbert problem about the higher order rogue wave and analyzed the near-field and far-field asymptotics by the Deift–Zhou nonlinear steepest descent method [6, 7].Afterwards, the robust inverse scattering method has been used to many other integrable equations, such as, the higher order soliton solutions of the NLS equation and the corresponding asymptotic analysis[8,9],the rogue wave to the Hirota equation[10]and the higher order NLS equation[11–13]and the discrete system [14].But to our best knowledge, we have not seen that the robust inverse scattering method was applied to the complex mKdV equation, thus we would like to study it.

It is well known that the mKdV equation and the nonlinear Schrödinger equation (NLS) are all the special flows of the AKNS system, thus they possess many similar properties, but they has some difference in essence.A typical characteristic is that the mKdV equation possesses the higher order dispersion term, which affects the shape of the solutions directly.In addition, we observe that mKdV equation has the nonzero constant solution, while the NLS equation has not.What the solution behavior will be under the constant background?Is it the soliton solution under the nonzero background? Or is there some other novel phenomena? With these questions in mind, we begin our research and analyze this kind of solution more profoundly.

The outline of this paper is as follows: in section 2, we give the classical inverse scattering method to mKdV equation (1) with the zero background and the nonzero constant background.Afterwards, we construct the higher order soliton solution and give a simple asymptotic analysis for larget.In addition, we also give the higher order rational travelling waves under the constant background,which are all shown in section 3.The last part is the conclusion.

2.Inverse scattering method for mKdV equation

For simplicity, we adopt the zero background and nonzero background condition as

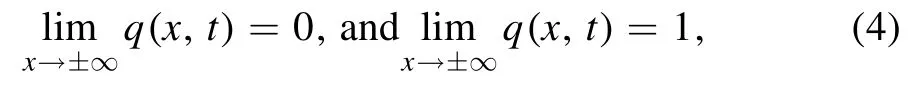
then the fundamental solution of the spatial Lax pair are

It can be seen that, the fundamental solutionψs,bgis analytic in the complexλ-plane,but theψr,bghas the singularities atλ= ±i.The Jost solution of equation (1) are defined uniquely with the boundary condition

where

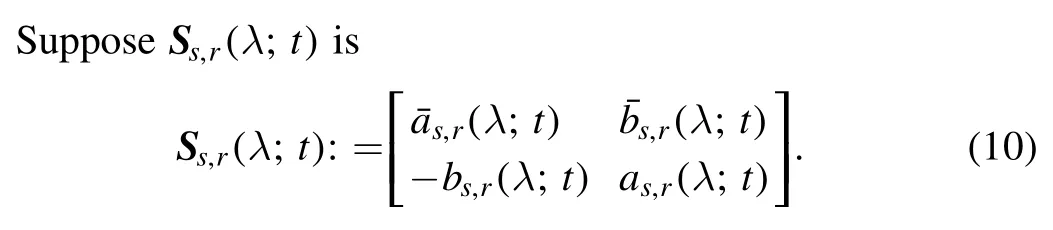
With a simple calculation, we have

2.1.Symmetry

From the symmetry about the spatial Lax pairU(λ;x,t)

which implies that the scattering dataas,r(λ;t)andbs,r(λ;t)obey the evolution behavior

Next, we begin to discuss the inverse scattering transformation.

2.2.Inverse scattering transformation

With the different analysis of the Jost solution(7),the Beals–Coifman solutions for the zero and nonzero background of the Lax pair(2)are the sectionally meromorphic function defined as follows:

In order to give the corresponding Riemann–Hilbert problem,we introduce the following matrices

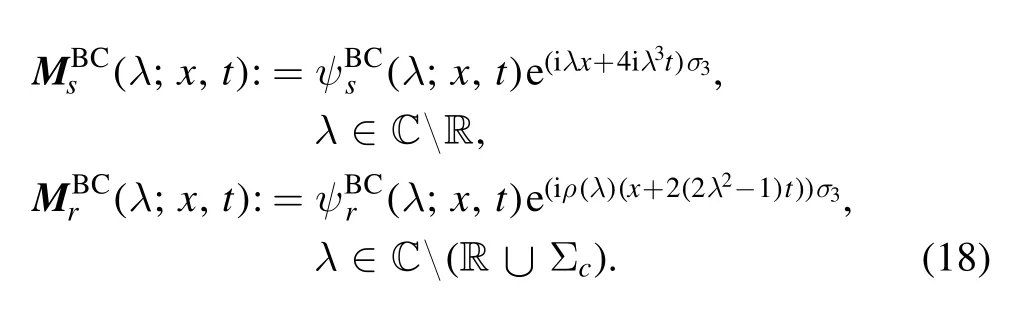
where

Forλ∈Σc,similar to the result in [5], we give the jump conditions aboutMr(λ;x,t),that is

where

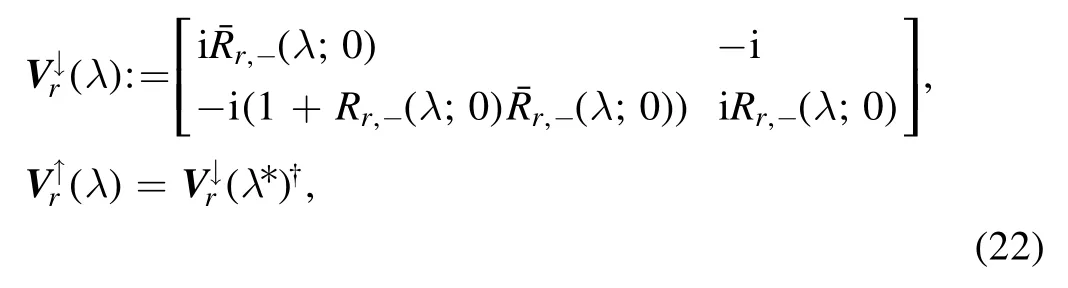
3.Robust inverse scattering and higher order soliton and rational traveling waves

Next, we will construct the soliton solutions and the rational traveling waves through the Darboux transformation and then give the corresponding Riemann–Hilbert problem about these higher order solutions.

3.1.Darboux transformation in the robust inverse scattering transformation

In this section, we want to construct the higher order soliton and higher order rational traveling waves with the Darboux transformation and the Riemann–Hilbert problem.Suppose the Darboux transformation as

Under this case, the new matrices satisfy the following jump conditions:

Remark 1.If the spectral parameterλ1in the Darboux transformation (30) is a pure imaginary number and the constant vectorcis real, then the potentialqr,s(x,t)via the limit calculation (25) will be a real number.Under this constraint, the complex mKdV equation (1) will become a real mKdV equation.

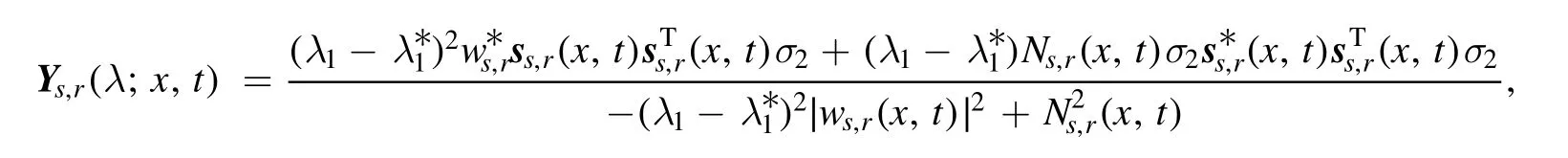
Remark 2.From the definition ofwe know

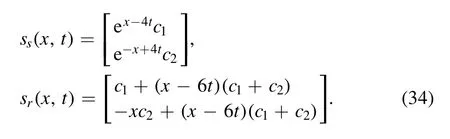
Whenc1+c2=0,sr(x,t)can be simplified into a simple formula, so as to theNr(x,t)andwr(x,t).Then the rational traveling waves will be changed into the first order case, but the soliton does not have a similar property.As a result,using this kind of Darboux transformation, we can get the evenorder soliton, if we want to get the odd case, we should use the first order soliton solution as the fundamental solution to iterate, but we do not give it in this paper.

By choosing special spectral parameterλ,1we can get the soliton solution and the the rational traveling waves.

Example 1.Settingλ1= i andc=[1, -1]Tin the zero background, we can get the second order soliton solution as

3.2.The Riemann-Hilbert problem of higher order soliton and rational traveling waves

Based on the property 1, we can simplify the jump condition in the Riemann–Hilbert problem 1 and 2.By a direct calculation, we know that the Darboux transformation at(x,t) =(0 , 0) has a good decomposition, that is

then the jump conditions in Riemann–Hilbert 1 and 2 can be converted into

Next,we rewrite the Darboux transformation as another equivalent formula and then rewrite the potential as a determinant.Suppose the N-fold Darboux transformation as

whereKs,r,j(x,t),Rs,r,j(x,t),j= 1, 2 …,Nare unknown matrices to be determined.AfterN-fold Darboux transformation,whenλ∈D0,the inner solutionψs,r(λ;x,t)equal to

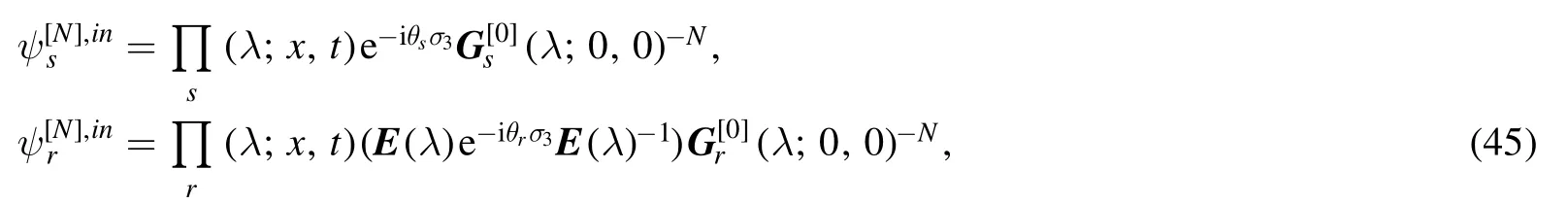
Under this situation, theN-order soliton and theN-order rational traveling waves can be changed into

For convenience,we introduce some notations about the series expansion coefficients so that the higher order solution can be given with a beautiful formula.Atλ= ±i, we have the following series expansion

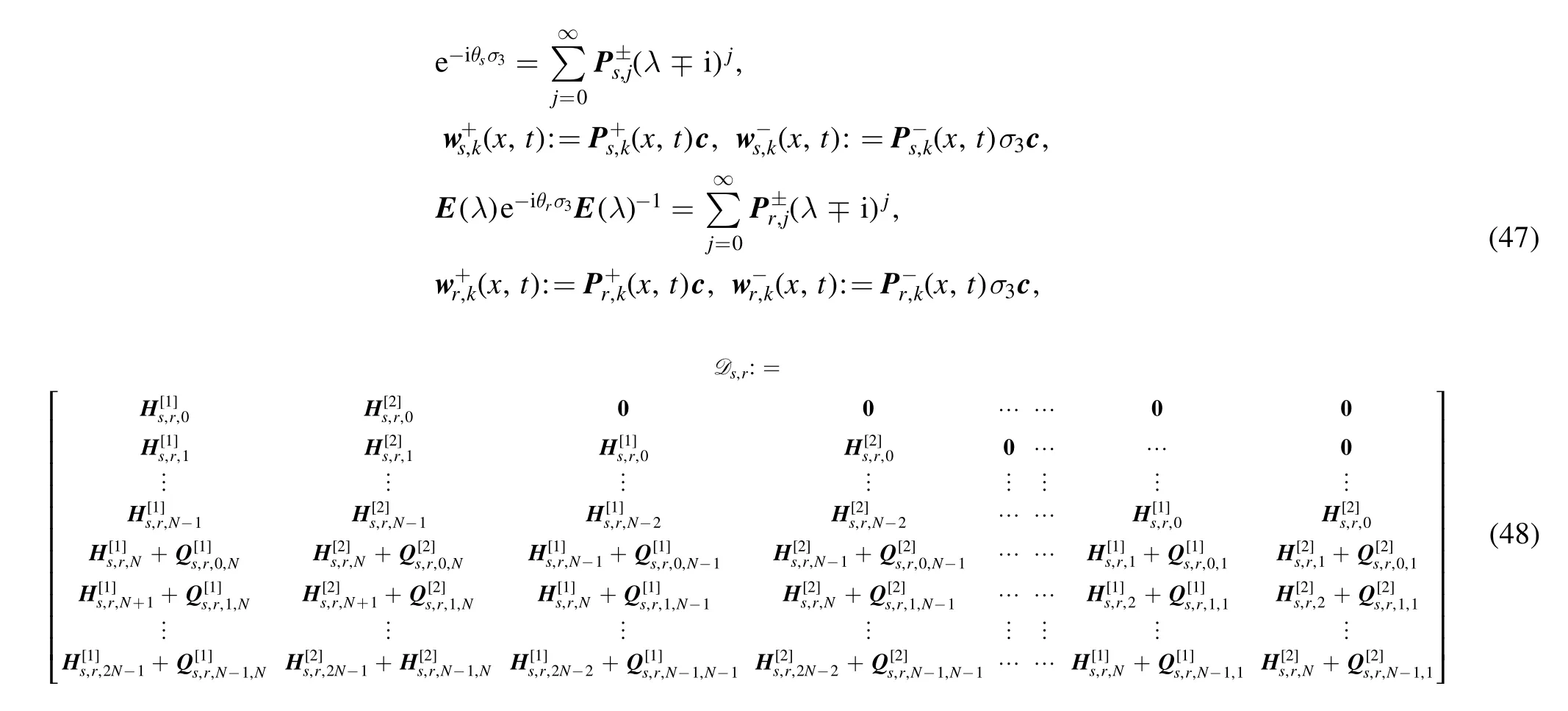
where

Under this formula, theN-order soliton andN-order rational solutions can be written as

3.3.Asymptotic analytic when t is large

As to the soliton solutions and the rational traveling waves, we give some figures by choosing some special order, which is shown in figures 2 and 3.

Figure 1.Definition of the regions D 0 , D±and the contour Σ 0= Σ+ + Σ-.

Figure 2.(a)–(c) The second order, fourth order and sixth order soliton for equation (1), respectively.

Figure 3.The upper ones are the odd-order rational traveling waves and the lower ones are the even-order rational waves for equation (1),whereξ is a new variable about x andt,ξ = x+6t .

From the soliton solution,we can see that whentis large,the higher order soliton will split into some single solitons,but as to the rational traveling wave,we can not receive a similar result from the figures and the exact expression in(37)up to now.Thus we only give the asymptotic expression about the soliton solutions.With the exact soliton solution in equation(35),if the soliton moves along the characteristic curves

then the soliton solutions will not approach to zero, otherwise, it will vanish.Substitute this characteristic curves into equation (35) and let ∣t∣→∞, then we can get the asymptotic soliton solutions,

WhenN= 2, we know the characteristic curves can be set as

and its asymptotic expression is

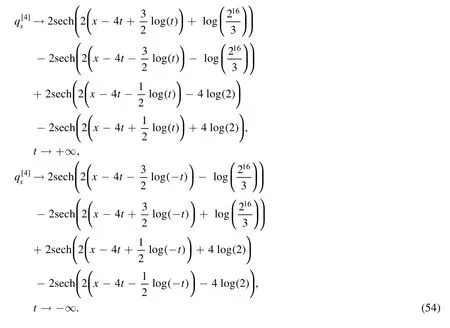
Remark 3.Following this rule of characteristic curves, for a general2N-order soliton, the characteristic curves can be set as

As to this result, we only give some comparison graphs between the exact solutions and the asymptotic solution fortpositive, the negative one can be given similarly, which is shown in figure 4.

Figure 4.(a)–(c) The comparison between the exact soliton solution and the asymptotic solution, when the corresponding order is second,fourth and sixth respectively.The blue solid line is the exact soliton, and the red dotted line is the asymptotic soliton.

4.Discussions and conclusions

In this paper,we construct two types of solutions to the mKdV equation, one is under the zero background condition and the other one is under the nonzero constant background.It is well known that the zero background soliton can be found for many integrable systems, such as the classical NLS equation.But the nonzero background soliton is very special, especially, in this paper, by choosing one fixed spectral parameter, we get the rational traveling waves.Although this type of solution is rational,it is very different from the well known rogue wave.Its shape is similar to the soliton,which is not a localized solution at the(x,t) -direction,which is very interesting.More importantly,the soliton solutions and the rational traveling waves are constructed under the framework of Riemann–Hilbert method,which can be used to discuss some asymptotic behaviors.In[6–9], the authors discuss the far filed and the near field asymptotics to the higher order soliton and the higher order rogue waves for the NLS equation.Comparing to the NLS equation, the phase term about the mKdV equation becomes more complex, which give a new challenge for study the asymptotics.After this paper, we will try to analyze this asymptotics and hope to get more interesting phenomena.

Acknowledgments

This work was supported by the Natural Science Foundation of Shandong Province (Grant No.ZR2019QD018), National Natural Science Foundation of China (Grant Nos.11975143,12105161, 61602188), CAS Key Laboratory of Science and Technology on Operational Oceanography (Grant No.OOST2021-05),Scientific Research Foundation of Shandong University of Science and Technology for Recruited Talents(Grant Nos.2017RCJJ068, 2017RCJJ069).