缺失数据下异方差半变系数模型的约束统计推断
2022-07-07张巍巍萨如拉冯三营
张巍巍, 萨如拉, 冯三营
(1.内蒙古农业大学理学院, 内蒙古呼和浩特 010018;2.郑州大学数学与统计学院, 河南郑州 450001)
1.引言
半变系数模型作为一类重要的半参数统计模型, 其一般形式为:

其中Y 是响应变量, 协变量Z ∈Rp, X ∈Rq, U为单变量, β = (β1,··· ,βp)T为p×1未知参数向量, g(·) = (g1(·),··· ,gq(·))T为q ×1未知函数向量.本文假设模型误差ε为异方差, 满足E(ε|X,Z,U)=0, Var(ε|X,Z,U)=σ2(U)>0.
目前模型(1.1)的估计问题已被统计学者广泛研究, 并且提出了很多不同的估计方法.[1−4]在对实际数据建模时, 模型有时会受到一些随机因素的干扰, 而使得模型误差ε可能会出现异方差, 针对异方差半变系数模型(1.1), 目前已有一些文献对其估计问题进行了研究, 比如,Ahmad等[3]给出了级数估计方法; KAI等[4]提出了半参数复合分位数回归方法; SHEN等[5]构造了模型参数和非参数分量的加权profile最小二乘估计量; YUAN和ZHOU[6]提出了模型参数和非参数分量的自适应加权估计量; ZHAO等[7]基于正交投影方法构造了模型参数和非参数分量的估计量; 当参数部分协变量Z带有可加测量误差时, ZHAO等[8]提出了参数和非参数分量的加权纠偏profile最小二乘估计量.
在实际应用中, 我们经常会遇到数据缺失的情形, 针对缺失数据下半参数回归模型的研究主要文献可参阅文[9-11].在本文中, 假设协变量Z随机缺失, 引入示性变量δ, δ =1表示Z可观察, δ =0表示Z缺失, 即在给定Y,X,U的情形下, Z和δ条件独立, 且满足

其中π(·)为选择概率函数.目前统计学者主要基于完全样本法、回归借补法和逆概率加权法研究了缺失数据下半变系数模型(1.1)的统计推断, 比如: 当响应变量Y 缺失时, WEI[12]在完全观察样本情形下, 利用经验似然方法研究了参数分量置信域的构造问题, 并针对参数分量的检验问题, 提出了修正的广义似然比统计量; 当响应变量Y 缺失且参数部分协变量Z与X分别带有可加测量误差时, 魏传华[13]与XIAO和LI[14]基于回归借补技术构造了模型参数和非参数分量的借补纠偏估计量; 当参数部分协变量Z缺失时, 陈盼盼等[15]基于逆概率加权法提出了模型参数分量的逆概率加权估计量, 并构造了参数分量的逆概率加权经验似然比统计量; XU等[16]在协变量Z缺失且带有可加测量误差时, 基于逆概率加权方法和纠偏方法构造了模型参数分量的逆概率加权纠偏经验似然比统计量.
在实际问题分析时, 除了样本信息以外人们基于历史研究等原因往往还会获得一些关于参数的先验信息, 这些先验信息有助于提高参数估计的精度.本文假设参数分量β满足:

其中A是k×p的已知矩阵, 且假设rank(A)=k, d是k×1的已知向量.目前有一些文献研究了复杂数据下半变系数模型(1.1)在约束条件(1.3)下的统计推断, 但是大部分文献仅考虑模型误差为同方差的情形, 比如: 魏传华和吴喜之[17]针对线性约束条件, 提出了profile拉格朗日乘子检验统计量, 当参数部分协变量Z带有可加测量误差时, ZHANG等[18]和WEI[19]基于线性约束条件, 提出了修正的约束估计量和修正的检验统计量, 当非参数部分协变量X带有可加测量误差时, FENG和XUE[20]提出了纠偏的约束估计量和纠偏的profile拉格朗日乘子检验统计量; 当协变量Z和X同时带有可加测量误差时, 樊明智和胡玉萍[21]提出了纠偏的约束估计量.
当模型误差为异方差, 为了得到模型参数分量和系数函数更有效的估计, 一些文献构造了半变系数异方差模型(1.1)的加权估计量和加权检验统计量, 比如; SHI和ZHAO[22]在参数分量Z带有可加测量误差的情形, 提出了加权纠偏的约束统计量和加权纠偏的profile拉格朗日乘子检验统计量, ZHANG和LI[23]在非参数分量X带有可加测量误差情形, 构造了模型参数分量和系数函数的加权纠偏约束估计量, 并针对线性检验问题, 提出了加权纠偏的profile拉格朗日乘子检验统计量.但到目前为止, 有关缺失数据下异方差半变系数模型在约束条件下的统计推断问题还未被研究, 因此本文研究协变量Z满足随机缺失条件(1.2)下, 异方差半变系数模型(1.1)在约束条件(1.3)下的估计问题.
2.自适应逆概率加权约束估计量


则模型(2.2)转化为

且极小化(2.3), 可得系数函数g(·)在u0点的估计

由上式可得M的估计为

将M的估计代入模型(2.4), 可得

基于上式和约束条件(1.3), 由拉格朗日乘数法, 构造辅助函数


则约束条件(1.3)下M的估计为
由(2.9)和(2.11), 可得模型误差ε的估计为


下面我们来处理缺失数据, 一般情形下选择概率函数π(·)未知, 因此需要去对它进行估计,但是利用非参数估计方法可能会产生维数灾祸, 为此本文借鉴文[15]的方法, 假设缺失机制为以下的Logistic回归模型


可得系数函数g(·)在u0点的自适应逆概率加权估计为

M的自适应逆概率加权估计为

其中

基于约束条件(1.3), 由拉格朗日乘数法, 构造加权辅助函数
下面给出估计量的渐近性质, 首先给出一些正则条件:
C1 随机变量U具有有界支撑Ω, 它的密度函数f(·)满足Lipschitz连续且在其支撑上有界且远离0, 并且具有二阶连续导数;


3.随机模拟
下面通过随机数值模拟来验证估计量的有限样本表现.考虑以下异方差半变系数模型:



表3.2 参数分量β2估计量的偏差(Bias)和均方误差(MSE)

表3.3 参数分量β3估计量的偏差(Bias)和均方误差(MSE)
从表3.1-3.3可以得到: 1)参数分量的所有估计量都是渐近无偏的, 当样本量的增大时, 估计量的绝对偏差和均方误差都在减小; 2)当缺失概率增大或异方差性增强时, 所有估计量的绝对偏差和均方误差都在增大; 3)当模型误差、缺失概率和样本量相同时, 本文提出估计量的均方误差在大多数情形下小于忽略缺失值估计量, 绝对偏差前者明显小于后者, 而且比忽略约束估计量ˆβ和忽略异方差估计量有更小的绝对偏差和均方误差.此外, 通过图3.1发现系数函数的自适应逆概率加权约束估计量与真实曲线比较接近.通过以上数值模拟验证了本文方法对缺失数据和异方差误差的有效性, 进一步说明了所提出方法的可行性.

表3.1 参数分量β1估计量的偏差(Bias)和均方误差(MSE)

图3.1 系数函数g1(u)和g2(u)的估计曲线图, 其中实线表示真实曲线, 点虚线表示本文提出的自适应逆概率加权约束估计.
4.定理的证明


所以

引理4.6假设条件C1-C8成立, 则当n →∞, 有

结合Slutsky定理和中心极限定理即可完成证明.
引理4.7假设条件C1-C8成立, β的自适应逆概率加权估计ˆβ是渐近正态的, 即

证
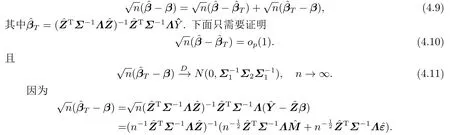
则由引理4.4-4.6, 结合条件C6, 由Slutsky定理即可完成(4.11)的证明.
下面证明(4.10) 式, 经简单运算可得

为此只需要证明

(4.12)-(4.15)式与文[5]中定理3中的证明类似, 结合定理2.1、引理4.1-4.2, 条件C6-C7即可完成证明, 这里略去.
定理2.2的证明由(2.19)式, 可得

因此由引理4.7结合Slutsky定理即可完成证明.
定理2.3的证明由(2.20)式, 经简单运算可得

对于∆1, 对u0邻域内的任意一点Ui, 对g(Ui)进行Taylor展开

则

由引理4.1, 结合定理2.1和引理4.2可证

结合(4.16)-(4.18), 由Slutsky定理即可完成证明.
