何 签，李顺初，董晓旭，夏 星，彭 春

（西华大学 理学院，四川 成都610039）

许多物理、化学、工程、生物中抽象出的数学模型可以转化为微分方程边值问题［1］，可见微分方程边值问题求解的重要性。针对不同的微分方程（组），其解的结构表达式也呈现出复杂性和多样性，因而微分方程（组）解的相似结构思想开始形成。李顺初［2－4］等分别对二阶线性常微分方程（组）的解进行探究，并提出了化解为统一的结构式的新方法——相似构造法。此方法可运用于Weber 方程［5－7］、Hermite 方程［8］、欧拉超几何方程［9］、复合变型Bessel 方程［10］、复合Bessel 方程［11］、复合Thomson 方程［12］及石油工程所涉及的渗流方程［13－15］中。

第一种Weber 方程是特殊函数重点研究的内容之一［16］，它在诸多重要学科（如流体力学、物理学等）中的应用极为广泛［6］。在量子力学中考虑一维谐振子问题时，可通过对定态Schrödinger 方程的变量进行代换，将其转换为第一种Weber 方程求解［17］，可见研究第一种Weber 方程的边值问题是很有必要的。文献［6－7］阐述了第一种Weber 方程和二区复合第一种Weber 方程的求解及应用，但却没有对三区复合第一种Weber 方程的解进行研究。为了进一步地探讨第一种Weber 方程的相关理论，本文研究如下三区复合第一种Weber 方程边值问题

其中：x所在区间均为闭区间；D，E，F，M，N，a，b，c，d，λ1，λ2，μ1，μ2是常数；ni(i＝1，2，3) 是整数，且ni(i＝1，2，3) ≥1，λ1λ2μ1μ2≠0，M2＋N2≠0，D≠0，0 ＜a＜b＜c＜d。

1 预备知识

其中：i＝1 代表内区(a≤x≤b)，i＝2 代表中区(b≤x≤c)，i＝3 代表外区(c≤x≤d)。

2 主要定理及其证明

定理1如果边值问题（1）有唯一解，则其内区、中区、外区解分别表示为

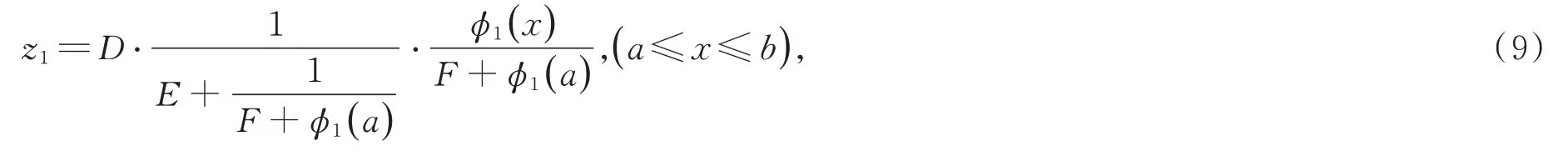
将（17）—（22）式组成一个关于待定系数A1，B1，A2，B2，A3，B3的线性方程组，结合（5）—（8）式，求得关于A1，B1，A2，B2，A3，B3的系数行列式为

3 相似构造法的步骤

第二步为内、中、外区相似核函数的构造。外区引解函数和外边界条件系数M，N 构成外区相似核函数，即式（12），同时算出ϕ3(c)；中区引解函数、衔接条件系数μ1，μ2及ϕ3(c) 构成中区相似核函数，即式（13），同时算出ϕ2(b)；内区引解函数、衔接条件系数λ1，λ2及ϕ2(b) 构成内区相似核函数，即式（14），同时算出ϕ1(a)。

第三步为边值问题（1）的解的获得。内边界条件系数D、E、F，内区相似核函数及ϕ1(a) 构成内区解，即式（9）；内边界条件系数D、E、F，衔接性条件系数λ1、λ2，内区引解函数，中区相似核函数及ϕ2(b) 构成中区解，即式（10）；内边界条件系数D、E、F，衔接性条件系数λ1、λ2、μ1、μ2，内区与中区引解函数，外区相似核函数及ϕ2(b)、ϕ3(c) 构成外区解，即式（11）。

4 相似构造法的应用

5 结论与认识

（1）相似构造法是求解边值问题（1）的一种简洁、准确、思路清晰的方法，只需找到第一种Weber 方程的2 个线性无关的解，并构造出相似核函数，再结合边界条件、衔接条件系数进行组装，边值问题（1）的解即可获得。

（2）相似构造法能够提升求解边值问题（1）的计算速度，以便能快速得到此类边值问题的解的相似结构。

（3）经过研究发现，当改变边界条件、交界面衔接条件系数时，边值问题（1）的解仍然呈现出相似结构，这更加说明了相似构造法在实际应用中的实用性和美观性。