乔世东

(山西大同大学数学与统计学院，山西大同 037009)

p-laplace 算子形式是φp(u,),=|s|p-2s,其中φp(s)=|s|p-2s,p＞1。

研究时间模上的一维p-Laplacian 两-点边值问题[1]

设p＞1，q＞1，且满足。另外，设

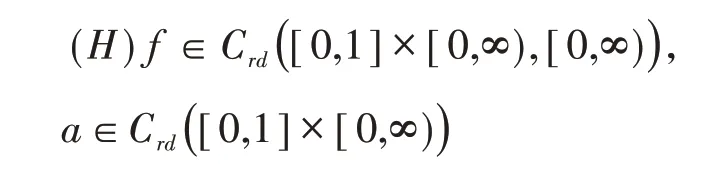
B1不增，B1(-V)=-B(V)，且有m＞0,B1(V) ≤mv2

记E=Crd()[0,1]T为一个Banach空间，其范数定义为，定义一个锥P⊂E，且

P={u∈E∶u(t)≥0，是凹函数不增，}

定义非负连续增函数λ,θ,α满足

对∀u∈P,有γ(u)=θ(u)≤a(u)。另外,

对∀u∈P,有‖u‖≤2γ(u),‖u‖=u(0)。

其中泛函λ，θ，α:P→R+,r,则

对∀u∈P,

有∀λ∈[0,1],θ(λu)=λθ(u)，

记

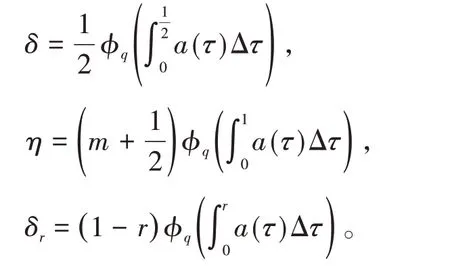
解方程得到

定义积分算子

AP⊂P,则A全连续积分算子，边值问题(1)有解u=u(t)当且仅当u是下列算子方程的解。

定理1(Avery-Henderson)设P是实巴拿赫空间E的一个锥,集合

如果ν,Φ是定义在P上的增加的,非负的连续函数,让θ是一个定义在P上非负的连续函数且有θ(0)=0 满足对一些正的常数r,M及所有的,Φ(u)≤θ(u)≤ν(u),‖u‖≤MΦ(u)。又假设存在常数0 ＜p＜q＜r满足下列条件θ(λu)≤λθ(u),0≤λ≤1,u∈∂P(θ,q)。假设A∶P是P上的一个全连续算子满足下列条件:

（1）Φ(Au) ＞r对所有的u∈∂P(Φ,r)；

（2）θ(Au) ＜q对所有的u∈∂P(θ,q)；

（3）P(ν,p) ≠φ,和ν(Au) ＞p对所有的u∈∂P(ν,q),

则A至少有两个不动点u1,u2满足

定理2设条件(H)成立,且又设存在常数a,b,c＞0,且满足，使

则边值问题1) 至少有两个正解u1,u2，满足α(u1)＞a,θ(u1)＜b,和b＜θ(u2),γ(u2)＜c[3]。

证明设

由假设条件(c3)得到

由定理1,则边值问题(1)至少有两个正解u1,u2满足.