李永艳, 杜 静

(沧州交通学院 通识教育学院, 河北 黄骅 061199)

关于染色问题,国内外许多学者在传统边染色、点染色和全染色基础上,增加相应的条件,提出了新的染色概念.Kalkowski M等[1]介绍了图的邻和可区别一般边染色,Przybylo等[2]进一步提出邻和可区别一般全染色概念,Flandrin等[3]在此基础上提出邻点扩展和可区别全染色,研究了路、圈、完全图、树等图的邻点扩展和可区别全染色,并提出一个猜想.张辉等[4-5]研究了星、扇、双星及联图的邻点扩展和可区别全染色.刘秀丽[6]讨论了Mycielski图的邻点可区别I-全染色,本文研究了路、圈、星、扇、轮的Mycielski图的邻点扩展和可区别全染色.

1 预备知识

定义2[6]对简单图G,若V(M(G))=V(G)∪V′∪{ω},

其中:V′={v′|v∈V(G)},{ω}∩(V∪V′)=∅,称图M(G)是图G的Mycielski图.

命题1[3]设Pm(m≥2)是m阶的路,则

命题2[3]设Cm(m≥3)是m阶的圈,则

egndi∑(Cm)=2

命题3[3]设Kn(n≥2)是n阶的完全图,则

egndi∑(Kn)=2

命题4[3]设T是n(n≥2)阶的树,则

egndi∑(T)≤2

猜想1(NESD猜想)[3]设G为简单图,则

egndi∑(G)≤2

文中未加说明的符号或术语可参见文献[7].

2 主要结果

定理1设Pn表示阶为n(n≥2)的路,则有egndi∑(M(Pn))=2.

证明设V(Pn)={v1,v2,…,vn},E(Pn)={v1v2,v2v3,…,vn-1vn},则

V(M(Pn))={v1,v2,…,vn}∪

{v′1,v′2,…,v′n}∪{ω}

E(M(Pn))={vivi+1|i=1,2,…,n-1}∪

{ωv′i|i=1,2,…,n}∪

{viv′j||i-j|=1,i,j=1,2,…,n}

令f是M(Pn)的一个全k-染色,显然M(Pn)没有NESD全1-染色,下面给出M(Pn)的一个NESD全2-染色.

情形1n=2.此时M(Pn)≅C5,由命题2得

egndi∑(M(P2))=egndi∑(C5)=2

情形2n≥3.此时所有边染颜色1,令f(ω)=1,f(vi)=1,i=1,2,…,n

则w(v′1)=w(v′n)=4,w(v′i)=6,i=2,3,…,n-1,w(v1)=4,

显然,f是M(Pn)的一个NESD全2-染色.

定理2设Cn表示阶为n(n≥3)的圈,则有

egndi∑(M(Cn))=2

证明M(Cn)即在M(Pn)的基础上添加3条边v1vn,v1v′n,v′1vn,

情形1n>3,n≡0(mod 4).此时M(Cn)与M(Pn)染色f相同,则w(v′i)=6,i=1,2,…,n,

显然,f是M(Cn)的一个NESD全2-染色.

情形2n>3,n≡1(mod 4).此时在M(Pn)染色f基础上,将f(vn-1vn)=1改为f(vn-1vn)=2,将f(v′n)=2改为f(v′n)=1 ,则w(v′i)=6,i=1,2,…,n

显然,f是M(Cn)的一个NESD全2-染色.

情形3n>3,n≡2(mod 4).此时M(Cn)与M(Pn)染色f相同,则w(v′i)=6,i=1,2,…,n

显然,f是M(Cn)的一个NESD全2-染色.

情形4n>3,n≡3(mod 4).此时在M(Pn)染色f基础上,将f(v′n-1vn)=1改为f(v′n-1vn)=2,则w(v′i)=6,i=1,2,…,n-2,n,w(v′n-1)=7

显然,f是M(Cn)的一个NESD全2-染色.

情形5n=3.此时设f是M(Cn)的一个全k-染色,令f(v′1)=2,其余点染颜色1,f(ωv′1)=f(v′2v3)=2,其余边染颜色1,则w(v1)=w(ω)=8,w(v2)=9,w(v3)=10,w(v′1)=w(v′3)=6,w(v′2)=7.

显然,f是M(C3)的一个NESD全2-染色.

定理3设Sn表示阶为n+1(n≥3)的星,则有egndi∑(M(Sn))=2.

证明设V(Sn)={v0,v1,v2,…,vn},E(Sn)={v0vi|i=1,2,…,n},则

V(M(Sn))={v0,v1,v2,…,vn}∪

{v′0,v′1,v′2,…,v′n}∪{ω}

E(M(Sn))={v0vi|i=1,2,…,n}∪

{v0v′i|i=1,2,…,n}∪

{v′0vi|i=1,2,…,n} ∪

{ωv′i|i=0,1,2,…,n}

设f是M(Sn)的一个全k-染色,显然M(Sn)没有NESD全1-染色,下面给出M(Sn)的一个NESD全2-染色.

令f(v′0)=2,其余点和所有边都染颜色1,则w(v0)=4n,w(vi)=5,i=1,2,…,n,w(v′0)=2n+2,w(v′i)=4,i=1,2,…,n,w(ω)=2n+3.

显然,f是M(Sn)的一个NESD全2-染色.

定理4设Fn表示阶为n+1(n≥3)的扇,则有egndi∑(M(Fn))=2.

证明M(Fn)即在M(Sn)的基础上添加边{vivi+1|i=1,2,…,n-1},{v′ivi+1|i=1,2,…,n-1},{v′ivi-1|i=2,…,n},设f是M(Fn)的一个全k-染色,显然M(Fn)没有NESD全1-染色,下面给出M(Fn)的一个NESD全2-染色.

情形1n≥3(n≠6).此时所有边都染颜色1,令f(ω)=f(vi)=1,i=0,1,2,…,n

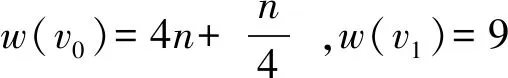
显然,f是M(Fn)的一个NESD全2-染色.

情形2n=6.此时在情形1的染色f基础上,将f(ωv′0)=1改为f(ωv′0)=2,则w(v′0)=14改为w(v′0)=15,w(ω)=16改为w(ω)=17.

显然,f是M(F6)的一个NESD全2-染色.

定理5设Wn表示阶为n+1(n≥3)的轮,则有egndi∑(M(Wn))=2.

证明M(Wn)即在M(Fn)的基础上添加边v1vn,v′1vn,v1v′n,

设f是M(Wn)的一个全k-染色,显然M(Wn)没有NESD全1-染色,下面给出M(Wn)的一个NESD全2-染色.

情形1n=3.此时令f(v′0)=f(v′2)=2,f(v0v1)=f(v1v3)=2,其余点和边都染颜色1,则w(v0)=14,w(v1)=16,w(v2)=13,w(v3)=15,w(v′0)=w(v′1)=w(v′3)=8,w(v′2)=9,w(ω)=10.

显然,f是M(W3)的一个NESD全2-染色.

情形2n>3且n≠6,n≡0,1,2(mod 4).此时令f(v0v1)=2,其余边都染颜色1,f(ω)=f(vi)=1,i=0,1,2,…,n

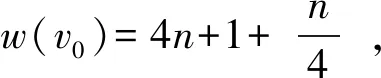
显然,f是M(Wn)的一个NESD全2-染色.

情形3n=6.此时在情形2的染色f基础上,将f(ωv′0)=1改为f(ωv′0)=2,则w(v′0)=14改为w(v′0)=15,w(ω)=16改为w(ω)=17.

显然,f是M(W6)的一个NESD全2-染色.

情形4n>3且n≡3(mod 4).此时在情形2的染色f基础上,将f(v′n-1vn)=1改为f(v′n-1vn)=2,则w(v′n-1)=8改为w(v′n-1)=9.

显然,f是M(Wn)的一个NESD全2-染色.

可以看出,猜想1对上述定理中的图M(Pn)、M(Cn)、M(Sn)、M(Fn)、M(Wn)是成立的.