张文娟

（闽南师范大学数学与统计学院,福建漳州363000）

1985年，Doignon 等[1]提出知识空间理论(Knowledge space theory,简称“KST”)[1],深受众多学者的关注.该理论通过分析学生对一系列问题的回答来确定学生的认知水平,因此在测评学生知识和个性化学习中起着举足轻重的作用.随后,众多学者对该理论进行了拓展.孙波等[2]提出了包含技能结构、技能空间以及技能层次等相关概念的扩展知识空间理论,Heller等[3-4]证明了一类特殊的CDMs(认知诊断模型)等价于概率知识空间模型论;Luca等[5-6]将二分知识空间的理论推广到了多分知识空间理论.

1982年，Wille[7]提出形式概念分析(FCA)理论,该理论是处理数据分析与规则提取的一种有效工具.属性约简作为其重要研究内容之一,它探讨了保持形式概念所有概念外延集不变的情况下，剔除冗余属性.针对属性约简的方式,张文修等[8]引入保持格结构不变的属性约简,Wu等[9]设计了形式背景的粒约简方法,Wang 等[10]研究了基于交(并)不可约元的概念格属性约简方法.通过对上述4 类约简理论的研究,Li等[11]指出了保持格结构不变与保持交不可约元的等价性.

1996年，Rusch 等[12]首次建立了知识空间理论与形式概念分析之间的联系.Spoto 等[13]以合取技能映射为研究对象,构建了合取技能映射与形式背景的联系.而后,李进金等[14]通过知识基构建了知识空间与形式背景的联系.Nicotra等[15]系统地分析了形式概念分析,知识空间理论与认知诊断理论的联系与区别.在此基础上,周银凤等[16]探讨了形式背景下的技能约简与评估,

本文旨在深入研究简单闭包空间和形式概念分析之间的联系,根据知识基的对偶集A 与形式背景中交不可约元的等价性,论证了合取模型下技能约简的实质是保持形式背景最小交式生成组不变的理论,而后给出了一种技能约简的方法,丰富了形式概念分析在知识空间中的应用.

1 预备知识

1.1 知识空间基本理论

定义1[17]设Q为非空问题集,K为Q的K一些子集构成的集族,若K包含∅,Q与其它知识状态.则称（Q,K）为知识结构,这里知识状态指的是个体在理想状态下能够正确答对问题集Q中的问题所构成集合.在问题域Q确定的情况下,可简称K为知识结构.

所谓理想状态指的是学生在没有受到外部压力或任何躁动情绪干扰的情况,没有因粗心导致的错误或侥幸猜对的情况.

定义2[17]设（Q,K）为知识结构,若K 有限,且对任意K1,K2∈K,有K1⋃K2∈K,则称（Q,K）为知识空间,或简称K为知识空间.

定义3[18]若G′是由G中所有有限个元素并构成的集合,则称集族G张成(span)G′,记为S（G）=G′.

由定义3 知,S（G）满足“并”封闭. 且一个“并”封闭集族F 的基是可张成F 的极小子集族B, 其中,B ⊆F.由于基的极小性,故∅∉B.类似地,知识基B 可张成K.需要注意的是:若K 为有限的知识空间,则K 有且只有一个知识基,对偶地L 也是有限的.基于上述知识,本文仅对有限条件下的知识空间与简单闭包空间进行研究.

定义4[18]设F是非空的集族,对于任意的q∈⋃F,称F中包含q的极小集为问题q的原子,记为σ(q).若对于某个q∈⋃F,X为q的原子,则称集合X∈F为一个原子.

通过定义4可知,问题的原子不唯一,在有限知识结构中,每个问题q至少有一个原子.若B是知识空间K的知识基,则B是由K中所有原子构成的集族[19].

定义5[19]设Q为非空问题集,S为非空技能集,τ:Q→2S{ ∅}.则称三元组（Q,S,τ）是一个技能映射.其中,对于任意的q∈Q,S的子集τ(q) 是与问题q求解相关的技能集.

事实上,对于给定的技能映射,主要有析取模型与合取模型两类.针对上述技能映射,在析取模型下有如下定义:若T为S的非空子集,则技能集T可确定的知识状态显然该模型表现为“或”的形式,即若T中存在某个与问题q求解相关的技能s∈T,则问题q属于技能集T确定的知识状态中.对偶地,合取模型下,技能集T可确定的知识状态此模型表现为“且”的形式,即技能集T只有包含与问题q求解相关的所有技能时,才有问题q属于技能集T确定的知识状态.

遍历S的全部子集分别可得析取模型与合取模型确定的知识结构,且在析取模型下确定的知识结构为知识空间,合取模型下确定的知识结构为简单闭包空间,二者是对偶结构.

1.2 形式背景基本理论

定义6[20]称三元组(U,A,I)为形式背景,其中是对象集,是属性集,I⊆U×A是U和A的二元关系.对于任意x∈U,m∈A,若(x,m)∈I则表示对象x有属性m;(x,m)∉I则表示对象x不具有属性m.

对任意X⊆U,B⊆A,记X*={m∈A:(x,m)∈I,∀x∈X};B*={x∈U:(x,m)∈I,∀m∈B}为Wille 定义的一对算子.

若二元组(X,B)满足X*=B和B*=X,则称(X,B)为(U,A,I)的形式概念.其中X和B分别称为形式概念的外延和内涵.所有形式概念的集合记为L(U,A,I),称为概念格.

定义7[21]若对于任意(X1,B1),(X2,B2)∈L(U,A,I), 引入二元关系“≤”定义两个概念间的偏序关系:(X1,B1)≤(X2,B2)⇌X1⊆X2(B1⊇B2).则其上、下确界定义如下:(X1,B1)∨(X2,B2)=((X1⋃X2)**,B1⋂B2);(X1,B1)∧(X2,B2)=(X1⋂X2,(B1⋃B2)**).且其下确界、上确界均为概念,从而L(U),A,I是完备格.

1.3 形式背景与简单闭包空间的联系

定义8[12]设Q={q1,q2,…,qm} 为非空问题集,qi∈Q为一个问题;S={s1,s2,…,sn} 为非空技能集,si∈S为一个技能,R为Q和S之间的二元关系,R⊆Q×S,则称三元组(Q,S,R)为(合取)技能映射(Q,S,f)相应的一个形式背景.且满足∀(q,s)∈R⇔s∉f(q),即技能s不能解决问题q,其中,f(q)表示析取技能映射下与问题q求解相关的技能集.

注由定义8可知,在合取模型下诱导的形式背景是一个反背景,其主要研究对象为问题和技能.特别地,本文称上述形式背景为技能背景.

定义9设(Q,S,R)是技能背景, 在问题集X⊆Q和技能集Y⊆S上定义如下运算:X*={s|s∈S,∀q∈X,s∉f(q)};Y*={q|q∈Q,∀s∈Y,f(q)⊆SY} .其中X*表示与X中所有问题求解无关的技能集,Y*表示与Y中所有技能都不能解决的问题集.

推论1若LQ(Q,S,R)为技能背景的全体外延集, 则LQ(Q,S,R)为简单闭包空间, 且有知识空间K={(QL)∈2Q|L∈LQ(Q,S,R)} .

证明由技能背景中概念的定义显然有∅,Q∈LQ(Q,S,R),任意(X1,B1),(X2,B2),其外延属于简单闭包空间,而概念本身满足交运算封闭,因此全体外延满足交运算封闭,即LQ(Q,S,R)为简单闭包空间.故知识空间K={(QL)∈2Q|L∈LQ(Q,S,R)} .

2 在简单闭包空间中知识基的对偶集A的构建

Spoto 等构建了合取模型与形式概念分析之间的联系,但并未对二者的联系进行深入的研究.基于上述研究,本文主要结合概念格中交不可约元的概念深入探讨二者的联系.

在已有的析取模型下,技能约简的核心是保持知识基不变,且若某个极小技能映射可确定知识空间当且仅当知识基的基数与极小技能集的基数相同.由简单闭包空间与知识空间的对偶性,首先探讨知识基对偶集A的构建.

推论2若（Q,L）是知识空间（Q,K）的对偶空间(即简单闭包空间),则对于任意q∈Q,问题q的原子可以表示为L中不包含问题q的极大知识状态集族的补集.

证明任意q∈Q,σ(q)为K 中包含问题q的极小状态集族, 根据对偶性有此时q不在的任何子集中且中任何子集均为不包含q的极大知识状态集族.故而问题q的原子可以表示为L中不包含问题q的极大知识状态集族的补集.

定义10设（Q,L）是简单闭包空间,对任意q∈Q,记δ(q)为L中不包含问题q的极大知识状态集族.

推论3若B为知识空间（Q,K）的知识基,记A={δ(q)|q∈Q} ,则有｜A｜=｜B｜,这里 |⋅|代表基数.

证明由于知识基可由Q中所有的σ(q)构成,而任意σ(q)⊆B,由推论2知存在δ(q)⊆A,满足σ(q)=遍历所有的问题q,根据对偶性显然有｜B｜=｜A｜.

定理1[19]若知识空间可由某个极小技能映射所确定当且仅当该知识空间有基,且知识基的个数与极小技能集的基数相同.此外,确定同一个知识空间的任意两个极小技能映射是同构的.同样地,可由任意技能映射所确定的有基的知识空间在其极小技能映射下仍可确定此空间.

定理2设（Q,L）与（Q,K）是同一个极小技能映射确定的简单闭包空间与知识空间,则（Q,L）可由该极小技能映射确定当且仅当A的基数与极小技能集的基数相同.

证明设技能映射为(Q,S,τ),任意s∈S,记K(s)为析取模型下技能{s} 确定的知识状态,L(s)为合取模型下技能{s} 确定的知识状态.则q∈K(s)⇌s∈τ(q)满足析取模型,q∈L(s)⇌s=τ(q)满足合取模型.对于任意L∈L,记T为S中可确定知识状态L的技能集,则对于任意问题q,有q∈L⇌τ(q)⊆T⇌∀s∈ST:且B ={K(s)|s∈ST} 为知识基.A={K′(s)|s∈ST} 恰为不包含问题的极大集.而由定理1 与推论3 可得A的基数与极小技能映射的基数相同.

例1设Q1={a,b,c,d,e} ,S1={s,t,u,v} ,定义技能映射为τ:Q1→2S1,其中τ(a)={s,t} ,τ(c)={v} ,τ(b)={t,u} ,τ(d)={s,v} ,τ(e)={t,u,v} .

经过计算可得:知识空间K={{a,d} ,{b,e} ,{a,b,e} ,{c,d,e} ,{a,b,d,e} ,{a,c,d,e} ,{b,c,d,e} ,Q1,∅},简单闭包空间L={{b,c,e} ,{a,c,d} ,{c,d} ,{a,b} ,{c} ,{b} ,{a} ,Q1,∅}. 此时知识基B ={{a,d} ,{b,e} ,{a,b,e} ,{c,d,e} }, A={{b,c,e} ,{a,c,d} ,{c,d} ,{a,b} }. 取L={c,d} , 则T={s,v} , 即其对偶其中,{a,b,e} ,{b,e} ∈B,{c,d} ,{a,c,d} ∈A.

3 交不可约元与知识基的对偶集的联系

由推论1 可知技能背景全体外延集构成了简单闭包空间,且简单闭包空间满足交封闭性.又因为基于知识基理论可探讨知识空间的技能约简问题.对偶地,本文考虑在简单闭包空间中寻找知识基的对偶集,在此基础上探讨简单闭包空间约简问题.实际上,文献[11]中提出保持交不可约元的概念格约简与保持格约简的结果一致.因此可从形式概念分析理论中交不可约元的概念出发,探讨A的构建问题.

2014年，李进金等[22]从交运算封闭性的角度提出了一种形式背景属性约简理论.形式背景(U,A,I)产生概念格L(U,A,I), 每个形式概念(X,B)的外延X构成集合:LU(U,A,I)={X|X⊆U,X**=X}, 同样地,LA(U,A,I)={B|B⊆A,B**=B}, 即LU(U,A,I)是不同的B∗的集合(B⊆A). 又因此,LU(U,A,I)又是{a∗|a∈A}经交运算形成的集合,于是{a∗|a∈A}可以看成是LU(U,A,I)的生成组.

命题1{s*|s∈S}是LQ(Q,S,R)的交式生成组,对任意L∈LQ(Q,S,R),存在S′⊆S,使得

定义11设(Q,S,R)为技能背景,若对于s∈S,存在s′∈S,使得s*=(s′)*,则称s与s′为同等技能.

事实上,同等技能在技能背景中的作用相同,因此将同等技能剔除后仍不影响A的构建.不妨记剔除后的技能集为S′,此时技能集中同等技能只保留一个.在此基础上,可探讨A的构造.

定义12设(Q,S,R)为技能背景,{s*|s∈S′}是LQ(Q,S,R)的交式生成组. 对任意s∈S′, 存在S″⊂S′,s∉S″,且则称s*为{s*|s∈S′} 的交可约元,否则称s*为交不可约元.

注意若s*为交可约元,则表示技能s是可约的.

性质1若s*为交可约元.记则有s*⊂(s′)*.

定理3设(Q,S,R)为技能背景,s*为{s*|s∈S′} 的交可约元,则对任意q∈Qs*,s*均不是不包含问题q的极大集.

证明s*为交可约元,由性质1 知任意q∈Q(s)*,存在s′∈S′s,使得q∈Q(s′)*⊂Q(s)*,s*⊂(s′)*,即s*均不是不包含Q中某个问题q的极大集.

定理4设(Q,S,R)为技能背景,si*为{s*|s∈S′} 中的交不可约元,则si*可表示为不含某个问题q的极大集.

证明对于任意si*为{s*|s∈S′} 交不可约元,存在某个问题q∈Qsi*且满足si*是不包含某个问题q的极大集.假设存在s1*为交不可约元使得对任意q∈Qs1*满足s1*不是不包含问题q的极大集.先证其中某个q∈Qs1*,至少存在一个si*,i≠1,且i≤ |S′|满足si*是不包含问题q的极大集.不妨假设存在技能s2∈S′,满足q∈Qs2*⊂Qs1*,s2*为不包含问题q的极大集.但此时有s1*⊂s2*,由交不可约元定义有s2*为{s*|s∈S′}的交不可约元.即s2*是交不可约元且是不包含问题q的极大集.类似地取遍Qs1*中所有元素,可得不包含问题的极大集必定为交不可约元.而Q不属于交不可约元,故在所有包含s1*的si*中,有如下情况成立:1)对于一切包含s1*的si*,有s1*⊂s2*⊂…⊂si*成立,其中2,…,i的次序依集合的包含关系排列,则对于任意但由真包含关系,必存在某个qi∈Q(s1)*,但qi∉Q(si)*,i≠1,也即(s1)*必是不包含某个问题qi的极大集.2)若对所有包含s1*的si*不存在真包含的关系,也即si*之间是不可比较的,则必有故对任意则有q∈Qs1*,但由真包含关系,必存在某个但故可表示为不含Q中某个问题的极大集.综上所述,即任意si*为{s*|s∈S′} 的交不可约元,则存在某个问题q∈Qsi*且满足si*是不包含某个问题q的极大集.

推论4设(Q,S,R)为技能背景,si*为{s*|s∈S′} 中的交不可约元,则Q(si)*均可表示含Q中包含某个问题的极小集.

图1 概念格L(Q,S2,R)Fig.1 The concept lattice L(Q,S2,R)

证明由推论2与定理4可得.

定理5设(Q,S,R)为技能背景,中的交不可约元,则技能映射在析取模型下确定的知识基B={Qsi*|si*}为交不可约元.

证明因为知识基可由所有包含问题的极小集构成,而由推论4知Q(s)*均可表示含Q中包含某个问题的极小集.而知识基由全体包含问题的极小集构成,遍历{s*|s∈S′} 中的全体交不可约元可得,知识基}为交不可约元.

例2设(Q2,S2,R2)是技能背景,其中Q2={a,b,c,d,e} ,S2={r,s,t,u,v,w} ,则由此技能背景构造的概念格如表1和图1.

记技能映射为τ(a)={r,t,u,v} ,τ(b)={s,u,v,w} ,τ(c)={t} ,τ(d)={t,u} ,τ(e)={u} ,从而得闭包空间L ={∅,{c} ,{e} ,{c,d,e} ,{b,e} ,{a,c,d,e} ,{b,c,d,e} ,Q2} , K={Q2,{a,b,d,e} ,{a,b,c,d} ,{a,b} ,{a,c,d} ,{b} ,{a} ,∅} 为与之相对应的知识空间.则知识基B ={{a} ,{b} ,{a,c,d} ,{a,b,d,e} },A={{b,c,d,e} ,{a,c,d,e} ,{b,e} ,{c} }.

技能概念如下:(r*,r**)=(b cd e,r),(t*,t**)=(be,rt),(s*,s**)=(w*,w**)=(a cd e,sw),(u*,u**)=(c,rsuvw),(v*,v**)=(cd e,rsvw).由上述知识知计算A 需要剔除技能s或者w,不妨假设剔除技能w后的技能集为S′2.此时有s*⋂r*=v*,故v*为交可约元.并且可验证对于a,b∈Q(v)*,有r*是不包含问题a的极大集,s*是不包含问题b的极大集.从而也知交可约元必定是不包含问题的极大状态集.剔除同等技能集后的交不可约元分别为r*,s*,t*,u*,显然r*为不含问题a的极大集,经过计算可得,{r*,s*,t*,u*} 均为不含某个问题的极大集.且其对偶B ={{a} ,{b} ,{a,c,d} ,{a,b,d,e} }恰为知识空间的基.

表1 技能背景(Q2,S2,R2)Tab.1 A skill context(Q2,S2,R2)

由推论4及知识基的定义知,知识基可由剔除同等技能后交不可约元的补集构成,但剔除同等技能后求交不可约元的方法比较繁琐.由于同等技能蕴含相同的信息,因此极小技能集的求解可转化为技能背景中的最小交式生成组的求解,也即极小技能集的求解可转化为形式背景中最小交式生成组的求解.

例3续例2,根据文献[22]所提方法求解极小技能集.

显然交式生成组为{r*,s*,t*,u*,v*,w*} ,且s*=w*;S2/R={[r*],[s*],[t*],[u*],[v*]};取等价类中代表元组成属性集S2′={r,s,t,u,v} ;对{s∗|s∈S2′} 中的s∗依 |s∗|由大到小排序为r*,s*,v*,t*,u*,且v*=s*⋂r*,故删去v.从而有最小交式生成组为{r*,s*,t*,u*} ,与例2结果一致.

4 技能约简

定义13设(Q,S,R)为技能背景,对于“↙”“↗”和“”,作出如下定义:q↗s表示(q,s)∉R并且s*是不包含q的极大集.q↘s表示(q,s)∉R并且q*是不包含s的极大集.qs表示同时满足q↗s与q↘s.

例4设(Q3,S3,R3)是技能背景,其中Q3={1,2,3,4,5,6} ,S3={a,b,c,d,e,f} ,则由此技能背景构造的概念格如表2和图2-图3.

表2 技能背景(Q3,S3,R3)Tab.2 A skill context(Q3,S3,R3)

图2 概念格L(Q3,S3,R3)Fig.2 The concept lattice L(Q3,S3,R3)

图3 概念格L(Q3,S3,R3)Fig.3 The concept lattice L(Q3,S3,R3)

图2与图3分别表示从技能出发构造的概念格与从问题出发构造的概念格,根据上述知识,技能约简保持交不可约元的外延集不变,类似地,问题约简是保持交不可约元的内涵集不变.而所在的行、列恰好为不包含某个技能的极大问题集与不包含某个问题的极大技能集,由第三部分知识可知,二者对应于问题集的最小交式生成组与技能集的最小交式生成组,因此剔除不含所在行、列恰好是保持问题集的最小交式生成组与技能集的最小交式生成组不变,故下面给出其约简方式，如表3-表4.

由于b与f所在列完全相同,故而删除其中之一对结果没有影响,故技能约简集为{a,b,c,d} .

由第3 部分知识,交式生成组{a*,b*,c*,d*,e*,f*} ,且b*=f*;S3/R={[a*],[b*],[c*],[d*],[e*]};取等价类中代表元组成属性集S3′={a,b,c,d,e} ; 对{a∗|a∈S3′} 中的a∗依 |a∗|由大到小排序为a*,b*,c*,d*,e*, 且e*=b*⋂d*,故删去e.最小交式生成组{a*,b*,c*,d*} ,即技能约简集为{a,b,c,d} .与利用的结果一致.

5 结束语

定义了知识基的对偶集A ,基于保持交不可约元外延集不变的属性约简理论,建立交不可约元外延集与A 的等价性.给出合取模型下技能约简的原理与概念格保持最小交式生成组不变的理论相同.进一步给出了技能约简的方法,但如何进一步将形式概念分析方法应用到知识空间,以及如何更深次挖掘它们之间的联系有待在将来的工作中不断完善.

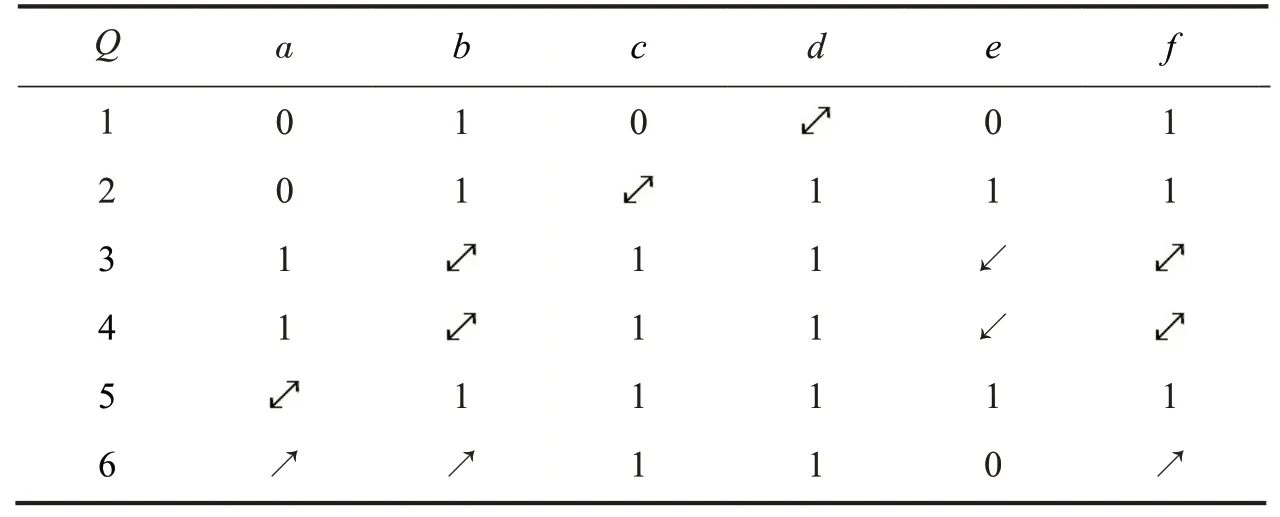
表3 转化后的技能背景Tab.3 skill context after coverted

表4 约简后的技能背景Tab.4 skill context after reduction