MULTIPLE SOLUTIONS FOR THE SCHRDINGER-POISSON EQUATION WITH A GENERAL NONLINEARITY∗
2021-06-17蒋永生
(蒋永生)
School of Statistics and Mathematics,Zhongnan University of Economics and Law,Wuhan 430073,China
E-mail:jiangys@zuel.edu.cn
Na WEI(魏娜)†
School of Statistics and Mathematics,Zhongnan University of Economics and Law,Wuhan 430073,China
Department of Mathematics and Statistics,Curtin University,GPO Box U 1987,WA 6845,Australia
E-mail:nawei2006@126.com
Yonghong WU(吴永洪)
Department of Mathematics and Statistics,Curtin University,GPO Box U 1987,WA 6845,Australia
E-mail:Y.Wu@curtin.edu.au
Abstract We are concerned with the nonlinear Schrödinger-Poisson equation where λ is a parameter,V(x)is an unbounded potential and f(u)is a general nonlinearity.We prove the existence of a ground state solution and multiple solutions to problem(P).
Key words Multiple solutions;ground state solution;Schrödinger-Poisson equation
1 Introduction
To study the Hartree-Fock system,a mean field approximation was used to deduce the following Schrödinger-Poisson equation:
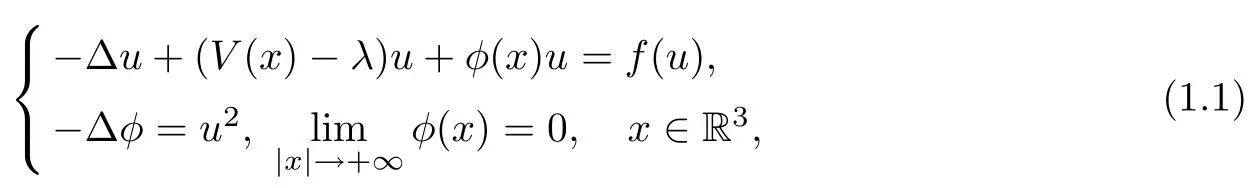
where λ is a parameter,V(x)is an external potential and f(u)is the nonlinearity.For more details on the physical aspects of the Hartree-Fock system and its approximation,we refer readers to[2,3,12–15,18,19,21]and the references therein.The harmonic potential V(x)=|x|2and the Slater term f(u)=|u|2/3u are more relevant from the viewpoint of the physics model(see[18,19]).Here,we consider the potential function and the nonlinearity with a more general application via the following assumptions:
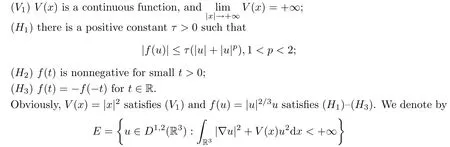
the Hilbert space with norm
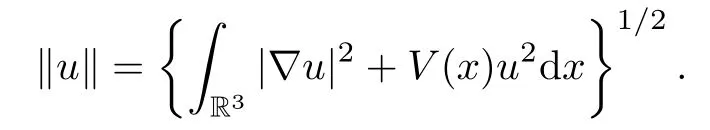
Under assumption(V1),we see that the embedding from E to Lp(R3)is compact for all p∈[2,6).Under assumptions(V1)and(H1),it is a standard process to prove that equation(1.1)is the Euler-Lagrange equation of a functional on E,which is defined by
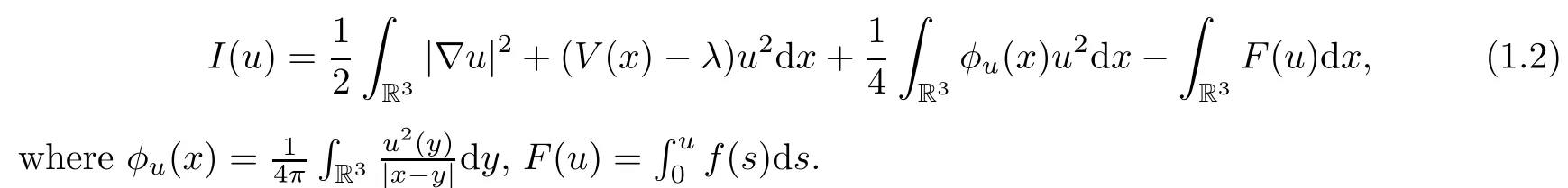
Problem(1.1)has been studied under various conditions in terms of the potential and nonlinearity;see[1,4,8–11,17,20,22]and the references therein.From the references mentioned above,the varied potentials V and nonlinearities f(u)give different geometric properties of I.Indeed,as f(u)=|u|p−1u with p≥3,the function I satisfies the(P.S.)condition,which means that any sequence{un}⊂H such that0 and{I(un)}is bounded and has a convergent subsequence(see[4]for V(x)−µ≡1 and[1]for a nonconstant potential V(x)).If f(u)=|u|p−1u with p∈(1,3),the geometric properties of I are more complex than for p∈[3,5).For example,we do not know whether I satisfies the(P.S.)condition when p∈(1,3).To overcome this difficulty,a related Pohozaev type equality is used to get a bounded approximate sequence to the solution of(1.1)with p∈(2,3);see[22].For the case f(u)=|u|p−1u with p∈(1,2),the symmetric properties of functions are used to prove that the(P.S.)condition of I holds when V(x)−λ=1,and therefore the existence of a radial symmetry solution is obtained;see[17].If there is a small parameter as the coefficient of the nonlocal term‘φuu’in(1.1),a truncated functional could be used to give a bounded sequence of approximate solutions to(1.1)without the radial symmetry constraint on the working functional space;see[11].For a nonconstant positive potential V(x)−λ and f(u)=|u|p−1u with p∈(1,2),an a priori estimate to the solution of(1.1)is given in[8]to prove the compactness of a sequence of approximate solutions to(1.1),so the existence of ground state solution is proved.
Under the general assumptions(V1),V(x)−λ is a sign-changing function for some λ.It is almost impossible to obtain an a priori estimate as in[8]to the solution of(1.1),although the nonlinearity f(u)possesses behavior similar to|u|p−1u with p∈(1,2).Since the coefficient of the nonlocal term in(1.1)is not a small parameter,it is not possible to construct a truncated functional as it in[11]to give a bounded sequence of approximate solutions.Motivated by the method in[6,9],we first prove that the functional of(1.1)satisfies the(P.S.)condition under assumptions(V1)and(H1),then via variational method,we study the existence of the ground state solution,the multiple solutions and the nonexistence of the solution to(1.1).
By assumptions(V1)and(H1),we see that I∈C1(E,R),by a standard method in[16].For any ϕ∈E,we have the Fréchet derivative of I as
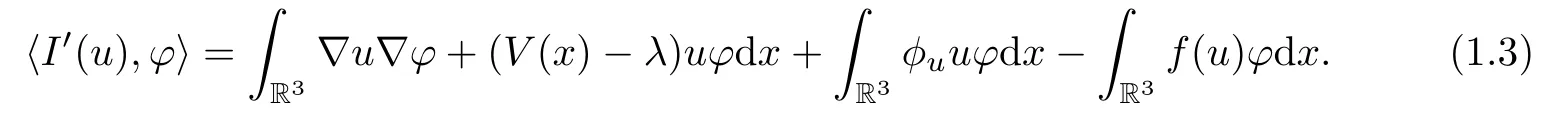
If I′(u)=0 in E−1,it is known that u is a critical point of I and thus a weak solution of(1.1).To make these notations more clear,we give the following definitions:
Definition 1.1u∈E is said to be a weak solution of(1.1)if
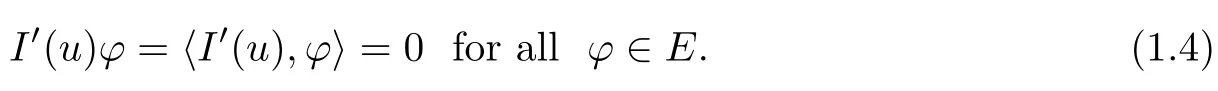
Definition 1.2Let G={u∈E{0}:I′(u)=0}.Then v is said to be a ground state solution to(1.1)if v is a weak solution of(1.1)and I(v)=
Before presenting our theorems,we state the following eigenvalue problem:
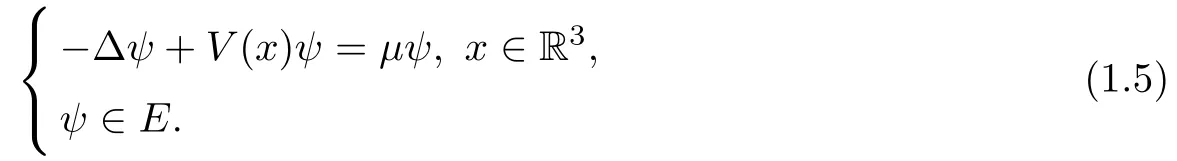
Under assumption(V1),eigenvalue problem(1.5)has infinite eigenvalues.Throughout this paper,we denote bythe normalized eigenfunctions of(1.5)corresponding to eigenvaluesthat is,|ψm|2=1 for any m∈N.It is well known thatµi→+∞as i→+∞andµ1<µ2≤µ3≤....
Our main results include three theorems.First,we prove that there exists a ground state solution of(1.1)as follows:
Theorem 1.3Assume that(V1)and(H1)–(H2)hold.If λ>µ1,then(1.1)has a ground state solution u∈E and I(u)<0.
To prove the existence of multiple solutions of(1.1),we need to introduce Clark’s theorem([16],Theorem 9.1),and to recall some notations about index theories.Let X be a real Banach space and let Γ={Y⊂X{0}:Y be closed and symmetric in regard to the original point}.For any Y∈Γ,we have a set Θ={k:k=1,2,...such that there exists an odd map ϕ∈C(Y,Rk{0})}.If Θ/=∅,we denote by γ(Y)=the genus of Y,otherwise γ(Y)=∞.Let γ(∅)=0.
Remark 1.4Let Sk−1be a unit sphere in the Euclidean space Rk.If Y⊂E{0}is homeomorphic to Sk−1by an odd map,then γ(Y)=k.
Proposition 1.5(See[16],Clark’s theorem) Let X be a real Banach space and let I∈C1(X,R)be even,bounded from below,and satisfying the(P.S.)condition.Supposing that I(0)=0,there is a set K⊂X such that K is homeomorphic to Sj−1by an odd map,andThen I possesses at least j distinct pairs of critical points,and the corresponding critical values are
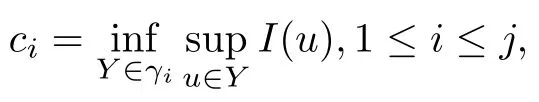
where γi={Y⊂X{0}:Y is closed and symmetric with respect to 0,γ(Y)≥i}.
By applying Proposition 1.5 to the functional I in(1.2),we obtain the following theorem:
Theorem 1.6Assume that(V1)and(H1)–(H3)hold.Ifµm<λ for some m∈N,there exist at least m pairs of distinct solutions±ujto(1.1).Moreover,I(±uj)<0 for 1≤j≤m.
We note that the potential V(x)under assumption(V1)may be a sign-changing function.The first author and his collaborator have studied the Schrödinger-Poisson equation with some sign-changing potentials in[7]by using the sub-supersolution method.Theorems 1.3 and 1.6 are supplemental to the previous research in[7].From Theorems 1.3 and Theorem 1.6,we see that(1.1)has nontrivial solutions when the parameter λ is greater thanµ1,which is the first eigenvalue of problem(1.5).It is natural to ask whether there exist nontrivial solutions of(1.1)for some λ<µ1.We partially answer this question in the next theorem,which requires the following assumption:
(V2):V(x)is nonnegative for x∈R3.
Roughly speaking,we have the estimate thatµ1≥0 under assumptions(V1)and(V2).
Theorem 1.7Assume that(V1)–(V2)and(H1)hold.Let τ>0 be given by(H1)andIf λ In this section,we prove that the functional I satisfies the(P.S.)condition under the assumptions(V1)and(H1).The next proof is based on the idea of[6,9],but there are some differences at certain points,since we consider a more general case here.For the convenience of the reader,we give the entire proof as follows: Lemma 2.1Assume that(V1)and(H1)hold.For any λ∈R,the sequence{un}⊂H1(R3)with I(un)≤C is bounded. ProofIt follows from−and the Young’s inequality that Let η=λ+θ.Then,by combining(1.2)and(2.3),we obtain that Let Ωη={x∈R3:V(x)<η}.If θ>0 is large enough,then,by assumption(V1),η>0 andΩηis a non-empty bounded set.Obviously,we see that Ωη⊂Ω2η.Since I(un)≤C,it follows from(2.4)that It follows that{|∇vn|2}must be bounded andHence{vn}is bounded in H1(R3).There exists v0∈H1(R3)up to a subsequence of{vn}such that Hence,v0(x)=0 a.e.x∈R3and the compact embedding theorem show that(Ω2ηis bounded,as mentioned above).These facts together with(2.7)imply that Thus{‖un‖}is bounded. □ Lemma 2.2Assume that(V1)and(H1)hold.Let λ∈R and{un}⊂E be a bounded(P.S.)sequence for functional I,that is,as n→+∞, Then{un}has a convergent subsequence in E. ProofUnder assumption(V1),the embedding ELq(R3)is compact for q∈[2,6)and there exists u∈Lq(R3)such that,up to a subsequence, Letting p be given by(H1)and n→+∞,it follows from(2.8)that By using Hölder’s inequality,we have On the other hand,it follows from(1.3)that In this section,we prove Theorems 1.3,1.6 and 1.7. Proof of Theorem 1.3Letµ1be the first eigenvalue of(1.5)and let ϕ1be the corresponding eigenfunction.ThenLetting h>0 be small enough,it follows from λ>µ1and(H2)that Let M={u∈E,I(u)<0},N={u∈E,I(u)≥0}.Then,by applying Lemma 2.1,E=M∪N and M⊂E is bounded.Since I is a continuous functional on E,we get that By assumption(H1)and the compactness of embedding ELq(R3)for q∈[2,6),we get that I is lower semicontinuous on E.Hence,there exists u0∈E such that Therefore,u0is a nontrivial critical point of I with minimal energy and u0is a ground state of(1.1). □ Proof of Theorem 1.6We see that,similar to(3.2),I is bounded from below.By applying Lemmas 2.1 and 2.2,we obtain that I satisfies the(P.S.)condition.It follows from assumption(H3)that the functional I is even.It is clear to see that I(0)=0.To apply Clark’s theorem in Proposition 1.5 with X=E to the functional I in(1.2),we construct the following setwhere ψiis the normalized eigenfunction of(1.5)related to the i-th eigenvalueµi:for any um∈Sm,we haveIt follows that Under the assumption that λ>µm,we haveLetting σ0>0 be small enough,from(3.4)we obtain that Let S={σ0u:u∈Sm}.Remark 1.4 implies the genus γ(S)=m.By(3.5),we obtain that Proof of Theorem 1.7Letting u∈E be a solution of(1.1),2 The(P.S.)Condition of Functional I
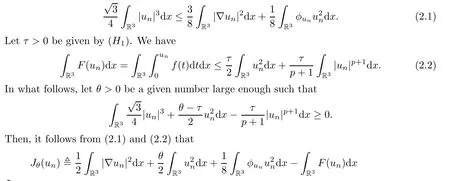
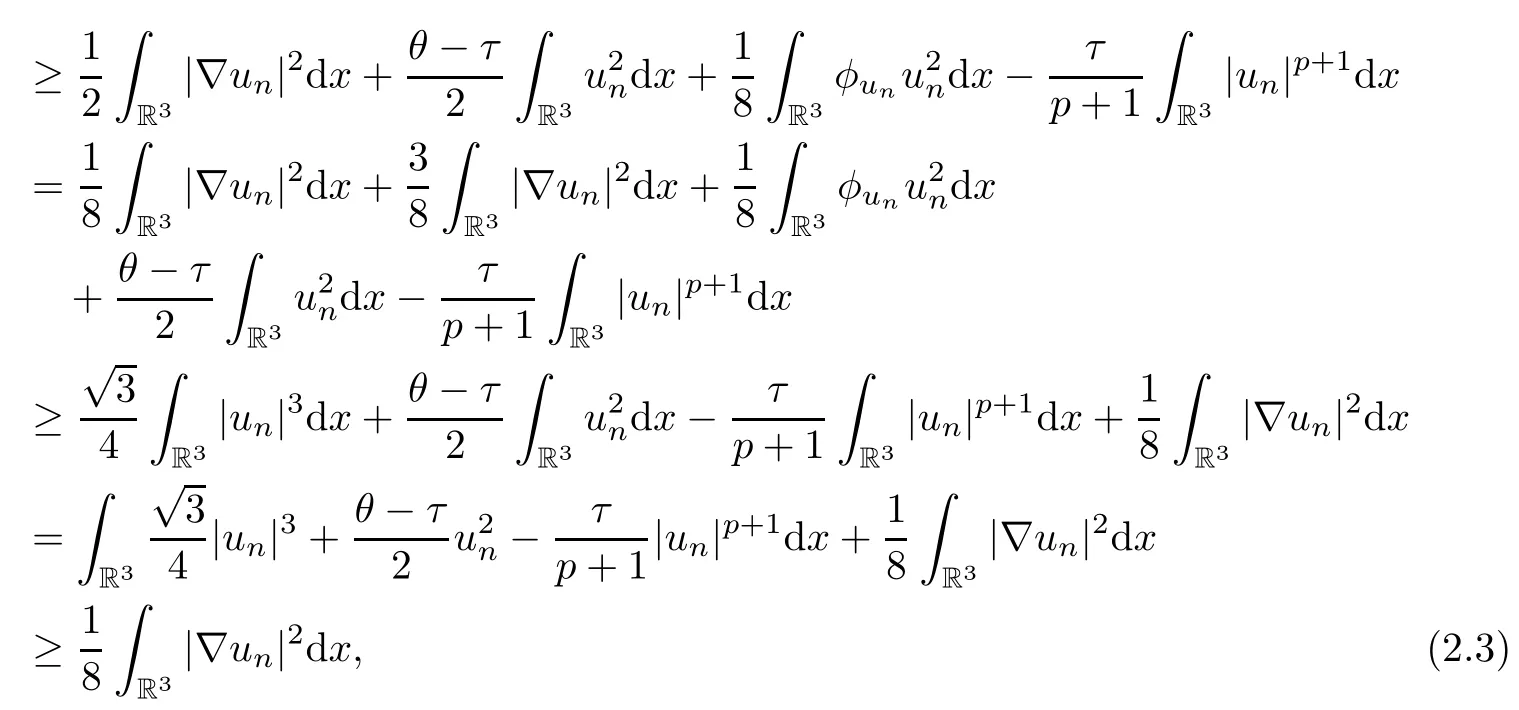
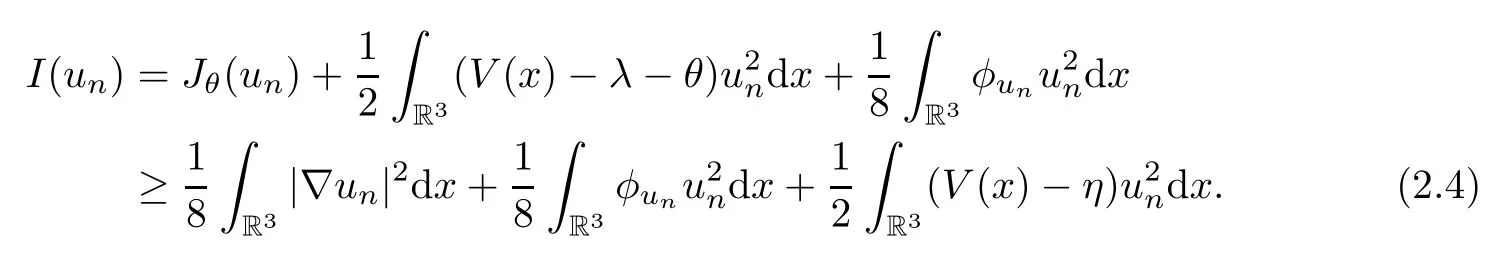

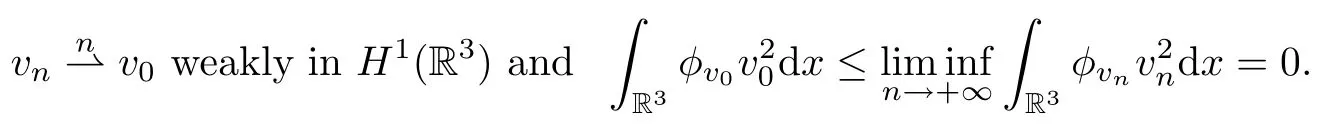
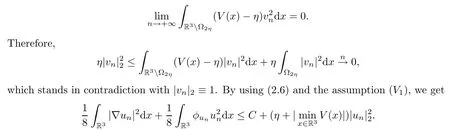
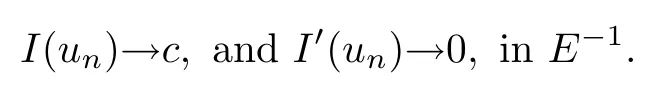

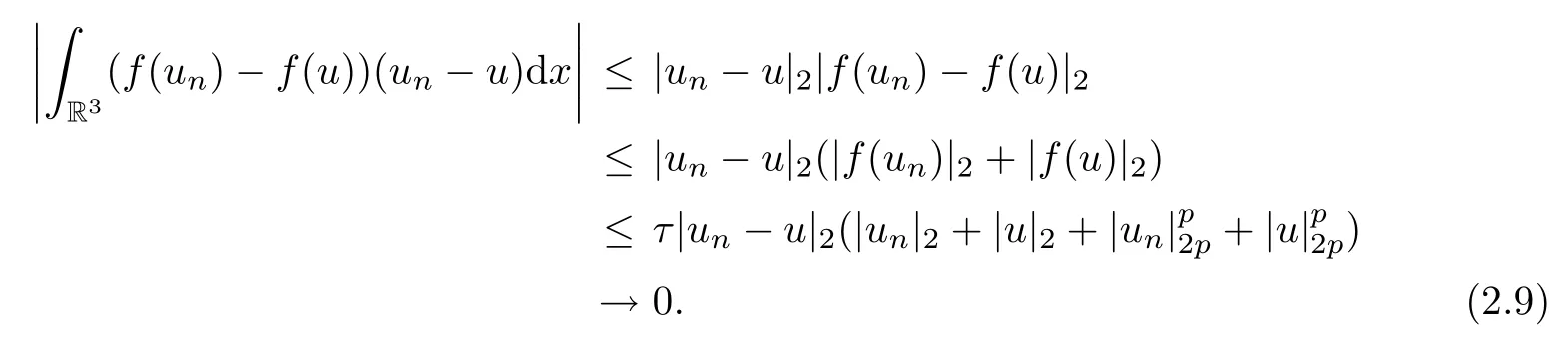
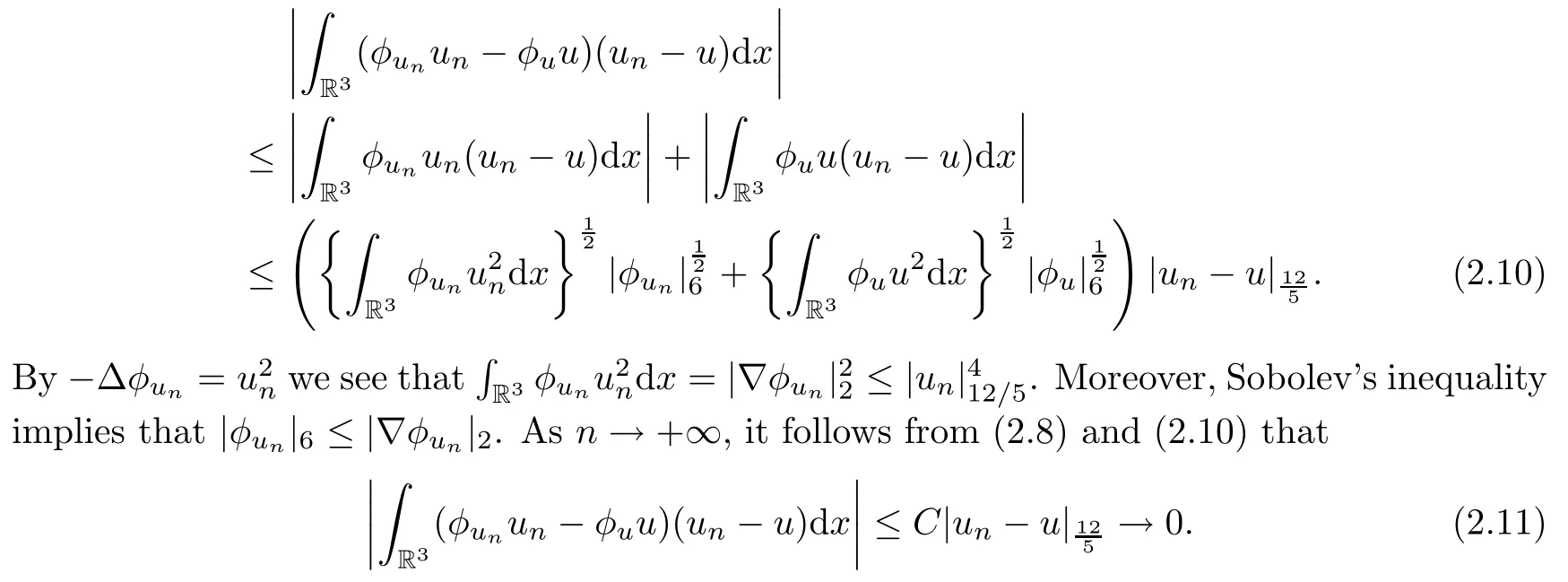
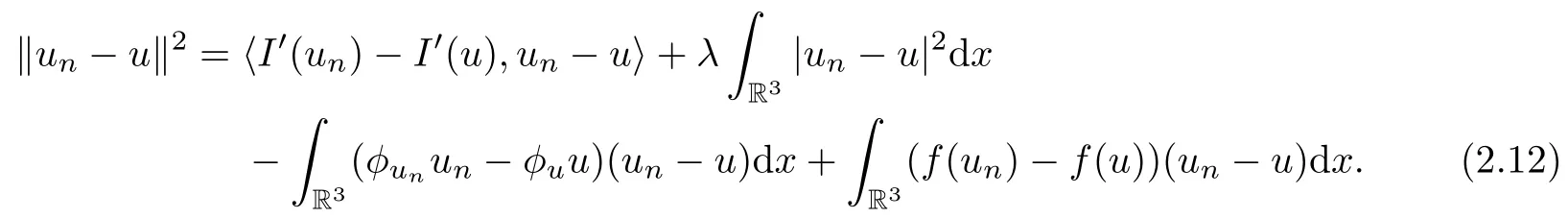
3 Existence of Ground State Solution and Multiple Solutions
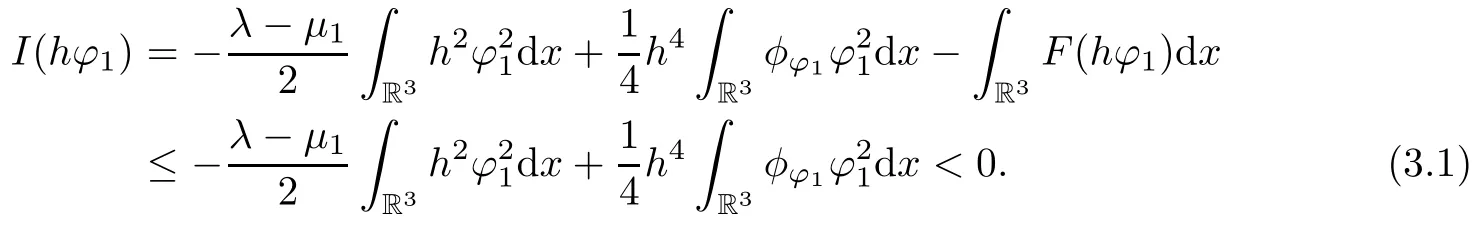
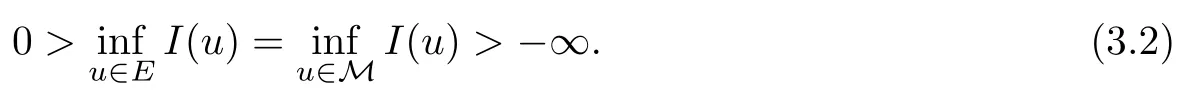
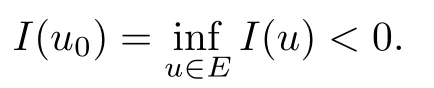
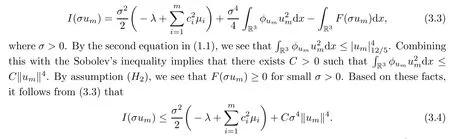
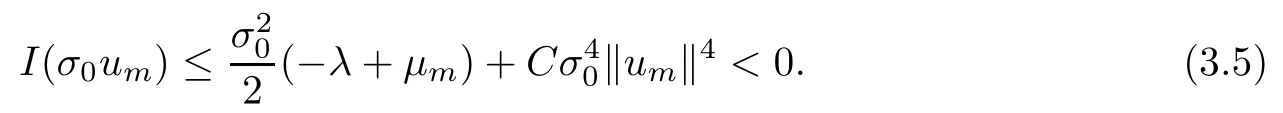

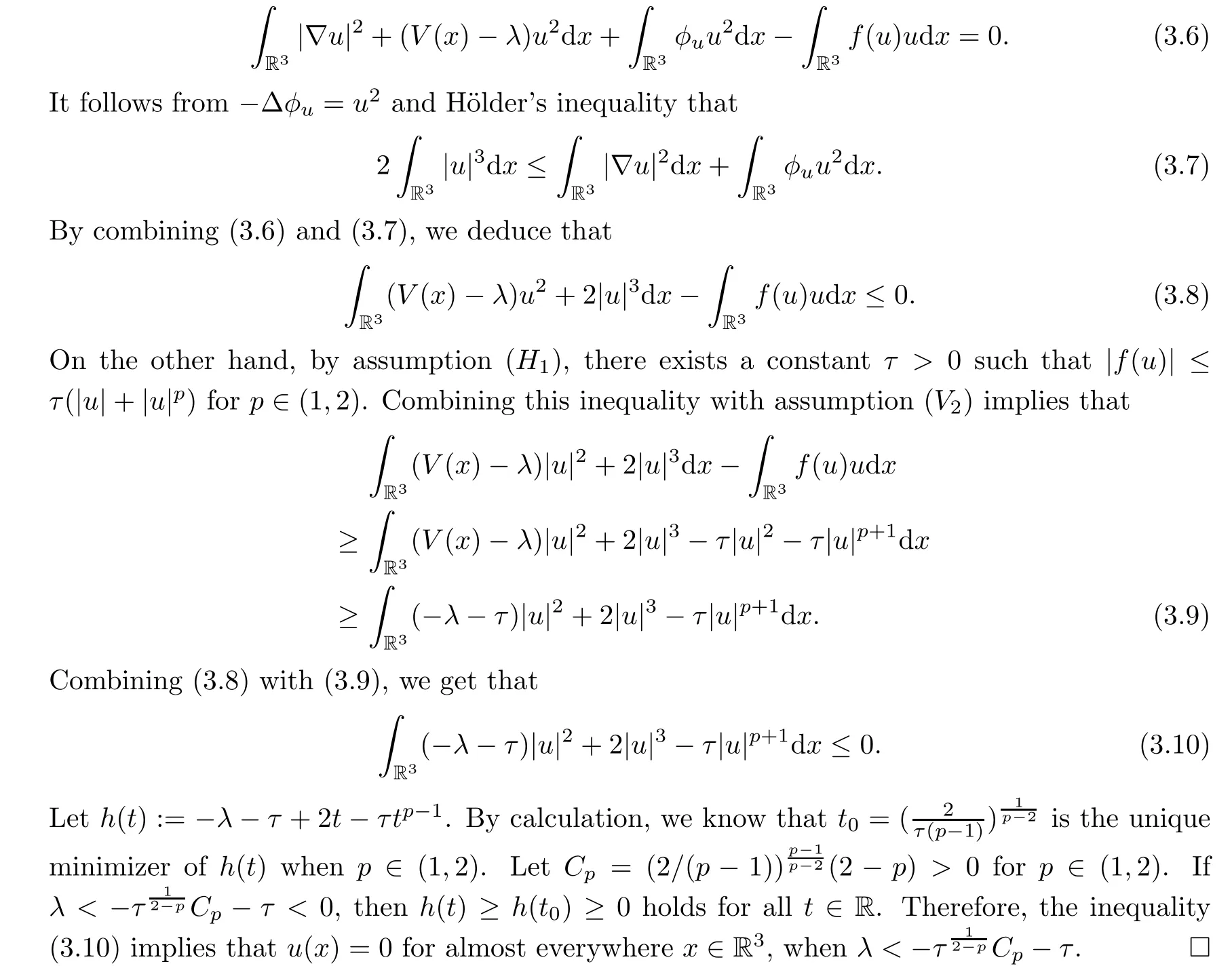
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- SEQUENCES OF POWERS OF TOEPLITZ OPERATORS ON THE BERGMAN SPACE∗
- A REMARK ON GENERAL COMPLEX(α,β)METRICS∗
- GLOBAL WEAK SOLUTIONS TO THE α-MODEL REGULARIZATION FOR 3D COMPRESSIBLE EULER-POISSON EQUATIONS∗
- HOMOCLINIC SOLUTIONS OF NONLINEAR LAPLACIAN DIFFERENCE EQUATIONS WITHOUT AMBROSETTI-RABINOWITZ CONDITION∗
- SHARP BOUNDS FOR TOADER-TYPE MEANS IN TERMS OF TWO-PARAMETER MEANS∗
- THE PROXIMAL RELATION,REGIONALLY PROXIMAL RELATION AND BANACH PROXIMAL RELATION FOR AMENABLE GROUP ACTIONS∗
