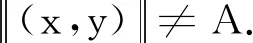于鹏艳， 侯成敏

( 延边大学 理学院，吉林 延吉 133002 )

0 引言

近年来，分数阶微分方程和微分包含耦合系统受到国内外学者的广泛关注，并得到了一些很好的研究成果.2017年，H.H.Alsulami等[1]研究了一类带有不可分的成对边值条件的Caputo型分数阶微分方程耦合系统

解的存在唯一性.其中:CDα和CDβ分别表示α阶和β阶Caputo型分数阶导数；f,g∶[0,T]×R×R→R；υi和μi是常实数，υiμi≠1,i=1,2.

2019年，B.Ahmad等[2]研究了一类带有边界条件的分数阶微分包含系统

解的存在性.其中：CDα和CDβ分别表示α阶和β阶Caputo型分数阶导数；F,G∶[0,T]×R×R→P(R)是多值映射，P(R)是R的所有非空子集全体；υi和μi是常实数，υiμi≠1,i=1,2.

2019年,B.Ahmad等[3]研究了一类分数阶混合微分方程系统边值问题

受以上文献启发，本文考虑一类新的混合Caputo型和Riemann-Liouville的分数阶微分包含耦合系统问题：

(1)

1 预备知识

定义1[4]设G∶X→P(X)为多值映射.多值映射的基本概念如下:

1)若对于所有x∈X，G(x)是凸(闭)的，则称P(x)为凸(闭)值的.

2)若对于任意的x0∈X，集合G(x0)是X的非空闭子集，且对于X中包含G(x0)的每一个开集N，都存在一个x0的开邻域N0，使得G(x0)⊆N,则称G是上半连续的.

3)若对于每一个B∈Pb(X)，G(B)是相对紧的，则称G是完全连续的.

4)若对于每一个y∈R，函数t→d(y,G(t))=inf{|y-z|:z∈G(t)}可测，则称多值映射G∶[a,b]→Pc l(R)可测.

5)若多值映射G是全连续的，且具有非空紧值，则G是上半连续的当且仅当G有一个闭图,即：xn→x*,yn→y*,yn∈G(xn) ⟹y*∈G(x*).集合Gr(G)={(x,y)∈X×Y,y∈G(X)}表示G的图像.

定义3[5]定义函数f∶(0,∞)→R的r阶Riemann-Liouville分数阶积分为

其中t>0,r>0,Γ(r)为Gamma函数，右端积分在R+上逐点有定义.

定义4[5]定义连续函数f∶(0,∞)→R的r阶Riemann-Liouville分数阶导数为

其中r>0,n=[r]+1,[r]表示r的整数部分，等式右端积分在R+上逐点有定义.

定义5[5]连续函数f∶(0,∞)→R的r阶Caputo型分数阶导数可写成

定义6[5]若f(t)∈Cn[0,∞)，则

(2)

的解为

定义7函数(x,y)∈C2(J,R)×C2(J,R)是系统(1)的解，即该函数满足系统(1)中的成对边值条件，并存在函数f,g∈L1(J,R)使得f(t)∈F(t,x(t),y(t)),g(t)∈G(t,x(t),y(t))在J上几乎处处成立，其中:

2 主要结果及其证明

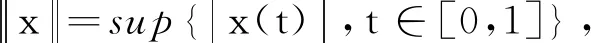
任取(x,y)∈X×X，并将SF,(x,y)={f∈L1([0,1],R):f(t)∈F(t,x(t),y(t)),a.e.t∈[0,1]}和SG,(x,y)={g∈L1([0,1],R):g(t)∈G(t,x(t),y(t)),a.e.t∈[0,1]}分别作为F和G的选择集.

根据引理1，将算子Θ1,Θ2∶X×X→P(X×X)定义为如下：

Θ1(x,y)={h1∈X×X:∃f∈SF,(x,y),g∈SG,(x,y)使得

h1(x,y)(t)=Q1(x,y)(t),对于∀t∈[0,1]},

(3)

Θ2(x,y)={h2∈X×X:∃f∈SF,(x,y),g∈SG,(x,y)使得

h2(x,y)(t)=Q2(x,y)(t),对于∀t∈[0,1]}.

(4)

其中:

(5)

(6)

(7)

(8)

(9)

引理2[4]若G∶X→Pc l(Y)是上半连续的，则Gr(G)是X×Y的一个闭子集.即：对于任意序列{xn}n ∈N⊂X和{yn}n ∈N⊂Y，当n→∞时有xn→x*,yn→y*，yn∈G(xn)，则y*∈G(x*).反之，如果G是完全连续的且有一个闭图像，则G是上半连续的.

在C([0,T],R)×C([0,T],R)上是一个闭图算子.

定理1系统(1)在[0，1]上至少有一个解，若以下假设成立：

(H1)多值映射F,G∶[0,1]×R2→P(R)是L1-Carathéodory多值映射，且具有非空紧值和凸值.

(H3)存在一个正数A满足AL>1，其中Mi(i=1,2,3,4)和L分别由式(5)—(9)给出.

证明取f∈SF,(x,y),g∈SG,(x,y)，则对于(x,y)∈X×X有:

因上式中h1∈Θ1,h2∈Θ2，所以(h1,h2)∈Θ(x,y).下面证明算子Θ满足Leray-Schauder型非线性选择定理的假设条件.

令0≤ω≤1，则对于每一个t∈(0,1)有:

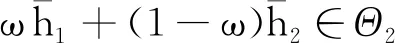
(10)

(11)

由于式(10)和式(11)分别是|h1|和|h2|的一个上界，因而可知|hi|(i=1,2)的上确界满足：

(12)

(13)

将式(12)和式(13)相加得

(14)

3)证Θ是等度连续的.取0≤t1

类似于上述的证明可得：

由上式可知，算子Θ(x,y)是等度连续的.再根据Arzelá-Ascoli定理可知，算子Θ(x,y)是完全连续的.

考虑连续线性算子Φ1,Φ2∶L1([0,1],X×X)→C([0,1],X×X),并做如下定义：

5)证明存在一个开集U⊆C([0,1],R),且对于所有的k∈(0,1)和(x,y)∈∂U都有(x,y)∉kΘ(x,y).令(x,y)∈kΘ(x,y)，其中k∈(0,1)，则存在f∈SF,(x,y)和g∈SG,(x,y)，且使得:

(15)

(16)

将式(15)和式(16)相加得

(17)