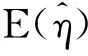张 洁

(云南民族大学 数学与计算机科学学院，云南 昆明 650500)

1935年，Landau等[1]首提描述连续统铁磁体自旋磁场演化的Landau-Lifshitz方程(简称LL方程)：

其中 ，λ1，λ2(>0)是常数.多年以来，既具有外加磁场又具有各向异性场的多维LL方程整体光滑解的存在性仍是重大的公开性问题.当外加磁场和各向异性场情形同时出现时，LL方程求解会面临一定的困难，许多研究者仅对外加磁场或各向异性场缺一情形进行研究.2000 — 2001年，Guo等[2-3]构造了n≥2维LL方程的一些显示柱对称解.2001年，Guo等针对2维柱对称情形构造了不存在外加磁场和各向异性场的LL方程的一族精确整体光滑圆盘解[4].2003年，Yang等[5]获得了存在和不存在外加磁场之间的一个精确显示解变换，利用此变换，可以构造出具有外加磁场的精确光滑柱对称解，类似地，此变换也适用于仅具有各向异性场的情形.然而直到2009年，Yang[6]才考虑了存在脉冲型外加磁场和各向异性场的多维LL方程，并给出了2维情形的显示柱对称解.Mu等[7]研究了在保持与文献[4]相同解的情形下如何反求出外加磁场和各向异性场问题.2011年，杨干山等[8]给出了一种求解存在外磁场和各向异性场的LL方程的新方法，并构造了LL方程的一族球面锥对称解.本文主要研究的方程GLL是LL方程的一种典型形式.

1 具有多向效应场的二维柱对称Landau-Lifshitz方程

首先，引入含Gilbert项的具有多向效应场的Landau-Lifshitz方程

其中各向异性场H(u)=(2αu1,2αu2,2βu3)；外磁场H=(h1,h2,h3)；γ是非负参数；λ是正参数；边界条件g=(g1,g2,g3)∈C2,α(∂Ω;R3)∩(∂Ω;S2)；Ω⊂R2和常数α∈(0,1).

其次，将方程GLL整理化简，可得

(1.1)

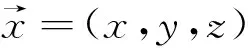
(1.2)

利用链式法则，柱坐标形式的拉普拉斯算子写成：

若考虑方程(1.1)的解仅与角度θ有关，则

(1.3)

根据方程(1.1)和(1.2)-(1.3)式，可得

(1.4)

(1.5)

其中B=h1ur+h2uθ+h3uz;

(1.6)

其中C=2α(1-(uz)2)+2β(uz)2;

(1.7)

(1.8)

和

(1.9)

将(1.3)～(1.9)式代入方程(1.1)，并整理化简为含Gilbert项的具有多向效应场的二维柱对称Landau-Lifshitz方程组

2 证明定理3.1所需的基本不等式和嵌入定理

(2.1)

(2.2)

和

(2.3)

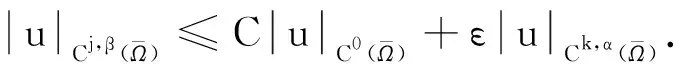
(2.4)

C=C(ε,j,k,Ω)，有下面不等式：

(2.5)

5) (Cauchy不等式[11])设对任意的a,b∈R，则有下面的不等式：

(2.6)

Ω⊆Rn，则有下面不等式：

(2.7)

其中当n=2时，ωn表示单位圆面积；当n=3时，ωn表示单位球体积.

(2.8)

8) (Hölder空间上的Sobolev嵌入定理[11])设对任意1≤p<∞和有界开子集Ω⊆Rn，

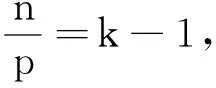
(2.9)

3 具有多向效应场的二维柱对称HLZ方程静态解的存在性

定理3.1的详细证明过程可由下面的这些引理提供：

设二维柱对称方程HLZ存在一个静态光滑解，如下所示：

(3.1)

由于边界条件g=(g1,g2,g3)∈C2,α(∂Ω;S2)∩(∂Ω;{uz=0})，因此在∂Ω上

将(3.1)式代入二维柱对称方程HLZ，通过直接计算和比较向量的各分量，得到下面2个方程：

(3.2)

和

(3.3)

(3.4)

和

(3.5)

(3.6)

和

(3.7)

证明将方程(3.6)重新改写成椭圆型方程:

(3.8)

(3.9)

(3.10)

(3.11)

(3.12)

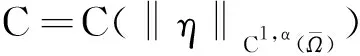
(3.13)

其中

(3.14)

(3.15)

(3.16)

2)再次考虑方程(3.7)，将其重新写成如下形式：

(3.17)

(3.18)

C3≥max{C1,C2}，使得

(3.10)式证明完毕.

3)为证明(3.11)式，再次考虑方程(3.7)，使其等价于下面方程:

(3.19)

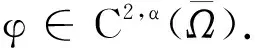
(3.20)

C6≥max{C4,C5}，使得

利用插值不等式(2.4)式，存在C7，使得

从而，存在C8，使得

(3.11)式证明完毕.

4)利用插值不等式(2.5)式，并结合(3.10)～(3.11)式，则(3.12)式成立.引理3.7证明完毕.

(3.21)

(3.22)

(3.23)

(3.24)

如果μ>max{μ1,μ2}，那么有估计

再次利用引理3.7，存在μ3≥max{μ1,μ2}，使得对于一切μ>μ3，有

第3步 由方程(3.6)和方程(3.22)，可得

(3.25)

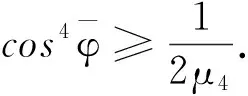
第6步 类似于引理2.3.7证明过程中的第3步，从方程(3.25)可知，我们有估计

(3.26)

引理3.8证明完毕.

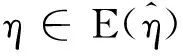
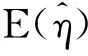
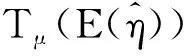
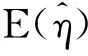
(3.27)

接着，考虑方程(3.6)，将其重新改写成如下形式：

(3.28)