郑文彬 ,李进金 ,张燕兰 ,廖淑娇

（1.闽南师范大学计算机学院，漳州，363000；2.闽南师范大学数学与统计学院，漳州，363000；3.福建省粒计算及其应用重点实验室，闽南师范大学，漳州，363000）

Qian et al［1］于2012 年提出多粒度粗糙集，在多粒度粗糙集中，目标决策可以通过多个粒度产生的信息粒进行刻画，因此可以从多个角度出发分析问题并获得更加满意、合理的求解，在许多多维度、多视角的现实生活问题中有强大的表示能力［2-4］.许多学者对多粒度粗糙集拓展模型进行了研究，例如Lin et al［5］提出多粒度邻域粗糙集，Dou et al［6］提出变精度多粒度粗糙集，张明等［7］提出可以自由控制粒度的可变粒度粗糙集等.

应用多粒度粗糙集时不可避免地存在冗余粒度，冗余粒度对多粒度粗糙集的各种应用没有帮助，反而因参与计算增加了计算时间.为解决这类问题有学者提出粒度约简的概念.Qian et al［1］首先提出一种启发式粒度约简算法，以粒度重要度为约简的依据.对于多粒度粗糙集，因悲观与乐观多粒度下近似集本身存在不同，粒度重要度有多种形式，而无论是何种粒度约简算法，粒度重要度都是粒度约简的核心［8-9］.现行算法多以悲观多粒度或者乐观多粒度粗糙集之正域作为衡量粒度重要性的指标，如孟慧丽等［10］考虑下近似分布约简，引入下近似分布约简中粒度集的信息量；汪小燕等［11］设计了可变粒度粗糙集的下近似分布粒度约简算法；张艳芹［12］在构建基于模糊等价关系的悲观多粒度模糊粗糙集模型的基础上，进一步给出粒度重要度的度量方法；于莹莹［13］提出相对粒度约简的概念并给出了基于相应的粒度重要性的粒度约简算法；桑妍丽和钱宇华［14］引入分布约简的概念并给出了相应的粒度重要度.这些基于正域或者下近似分布而提出的各种约简算法本质上都是保持下近似不变的算法.

本文尝试改进基于正域的算法，提出基于多粒度粗糙集上下近似集的粒度重要性度量.在粒度增加时乐观多粒度下近似集基数会变大，上近似集基数会减小；而悲观多粒度下近似集基数会变小，上近似集基数会变大.基于这些性质，以平滑系数为辅助项，提出两种粒度重要性度量.基于提出的粒度重要性度量，提出一种计算重要度的矩阵方法并设计相应的粒度约简算法，并使用UCI 数据验证了所提算法的有效性与优越性.

本文的主要贡献：

（1）提出保持乐观/悲观多粒度上下近似不变的约简方法，并提出了两种基于多粒度粗糙集上下近似集的粒度重要性度量；

（2）提出计算（1）中粒度重要性度量的具体矩阵方法；

（3）设计了两种启发式粒度约简算法；

（4）使用公开UCI 数据集进行实验，通过对比算法验证了所提计算方法和两种算法的有效性和高效性.

1 相关理论

定义1［1］令S=(U，AT，V，f，D)为一个多粒度决策信息系统，其中U={x1，x2，…，xn} 为非空有限论域，AT={A1，A2，…，Am} 为非空有限属性集族，A∈AT是一个属性集.为属性值的值域，VA为属性集A的值域.f：U×AT→V为一个决策函数，使得f(x，A)∈VA对任意的A∈AT，x∈U都成立.D={d1，d2，…，dr}为决策属性.

定义2［1］ 乐观多粒度粗糙集（Optimistic Multi-Granulation Rough Sets，OMGRS） 令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的X⊆U，X的乐观多粒度下近似集与上近似集分别表示为：

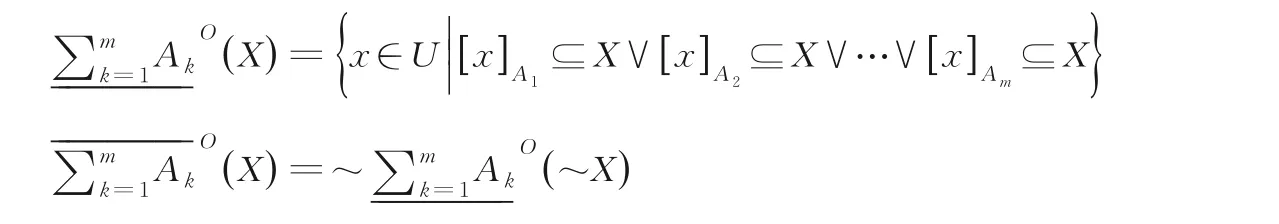
引理1［15］令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的X⊆U，X的乐观多粒度上近似集可以表示为：

定义3［1］ 悲观多粒度粗糙集（Pessimistic Multi-Granulation Rough Sets，PMGRS）令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的X⊆U，X的悲观多粒度下近似集与上近似集分别表示为：

引理2［15］令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的X⊆U，X的悲观多粒度上近似集可以表示为：

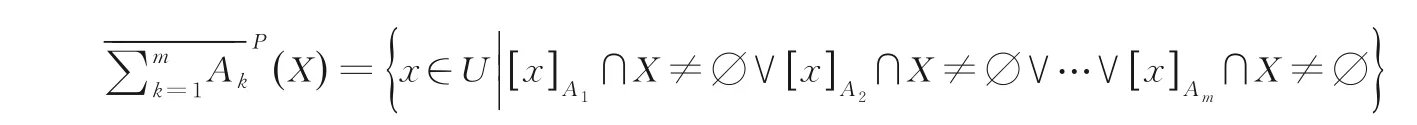
定义4［15］令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意X⊆U，X的向量矩阵表示为G(X)=[g1(X)，g2(X)，…，gn(X)]T，其中表示矩阵的转置.

2 基于多粒度粗糙集的粒度约简方法

定义5令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的x∈U，对于任意的BT⊆AT，BT的乐观不定、确定决策累计函数分别定义为：

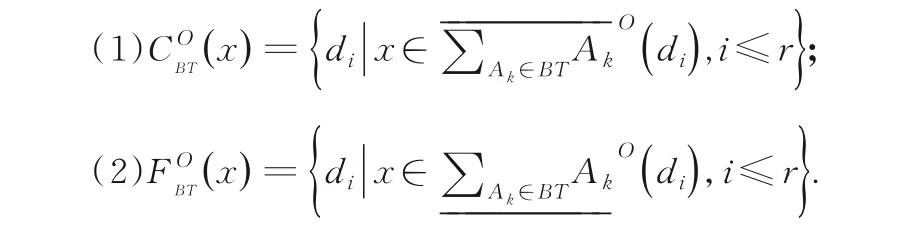
定义6令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的x∈U，对于任意的BT⊆AT，BT的悲观不定、确定决策累计函数分别定义为：

定理1令S=(U，AT，V，f，D)为一个多粒度决策信息系统.如果BT⊆CT⊆AT，则以下关于BT，CT的性质总是成立的：

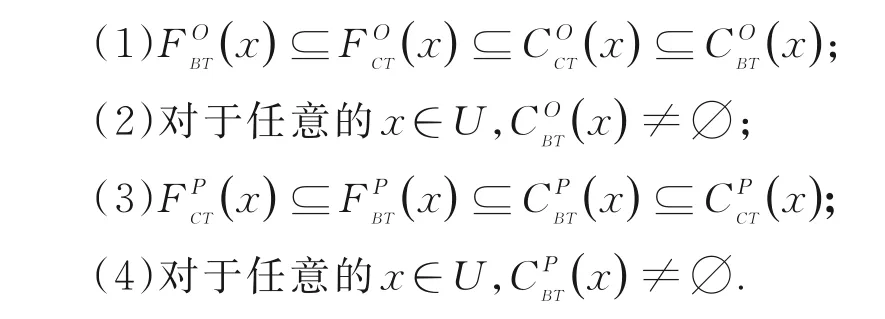
证 明

定义7令S=(U，AT，V，f，D)为一个多粒度决策信息系统.如果对于任意的x∈U，对于任意的BT⊆AT，若满足且则称BT为乐观累计决策粒度协调集.

定义8令S=(U，AT，V，f，D)为一个多粒度决策信息系统.如果对于任意的x∈U，对于任意的BT⊆AT，若满足且则称BT为悲观累计决策粒度协调集.

定义9令S=(U，AT，V，f，D)为一个多粒度决策信息系统.如果BT⊆AT，BT为乐观决策粒度协调集，若满足对于任意的CT⊂BT，CT不是AT的乐观决策粒度协调集，则称BT为AT的乐观累计决策粒度约简集.

定理2令S=(U，AT，V，f，D)为一个多粒度决策信息系统，如果CT为AT的乐观累计决策粒度约简集.以下结论总是成立的：

（2）证明类似（1）.

定义10令S=(U，AT，V，f，D)为一个多粒度决策信息系统.如果BT⊆AT，BT为悲观决策粒度协调集，若满足对于任意的CT⊂BT，CT不是AT的悲观决策粒度协调集，则称BT为AT的悲观累计决策粒度约简集.

定理3令S=(U，AT，V，f，D)为一个多粒度决策信息系统.如果CT为AT的悲观累计决策粒度约简集.以下结论总是成立的：

证 明 类似定理2.

定义11令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的BT⊆AT，BT的乐观平滑系数定义为：

定义12令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的BT⊆AT，BT的悲观平滑系数定义为：

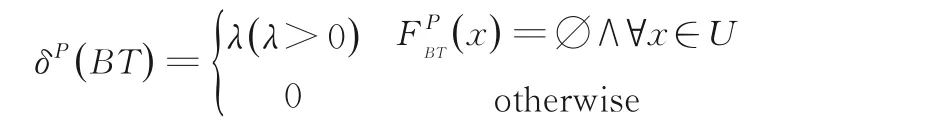
定义13令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的BT⊆AT，BT的乐观累计决策重要度定义为：

定义14令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的BT⊆AT，BT的悲观累计决策重要度定义为：

定理4令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的BT⊆CT⊆AT，以下性质总是成立的：

（1）γO(BT)≤γO(CT)；

（2）γP(BT)≤γP(CT).

证 明

(1)由定义2 与引理1，显然BT⊆CT⊆AT时，

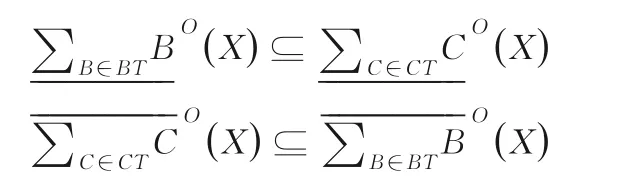
从而有γO(BT)≤γO(CT).

（2）由定义3 与引理2，证明类似（1）.

定义15令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的BT⊆AT，Ak∈BT，Ak的乐观粒度内重要度的定义为：

定义16令S=()

U，AT，V，f，D为一个多粒度决策信息系统.对于任意的BT⊆AT，Ak∈BT，Ak的悲观粒度内重要度的定义为：

定义17令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的BT⊆AT，Ak∉BT，Ak的乐观粒度外重要度的定义为：

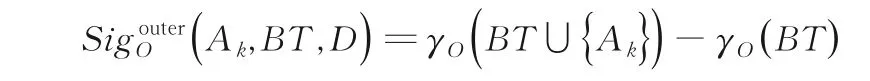
定义18令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的BT⊆AT，Ak∉BT，Ak的悲观粒度外重要度的定义为：

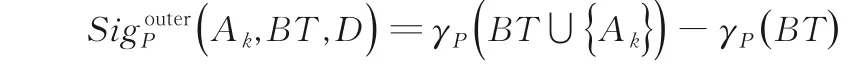
定义19令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的Ak∈AT，若满足，则称Ak为乐观核心粒度，而所有乐观核心粒度组成的集合称为乐观核心，记为COREO.

定义20令S=(U，AT，V，f，D)为一个多粒度决策信息系统.对于任意的Ak∈AT，若满足，则称Ak为悲观核心粒度，而所有悲观核心粒度组成的集合称为悲观核心，记为COREP.

定义21令S=(U，AT，V，f，D)为一个多粒度决策信息系统.粒Ak的特征矩阵定义为，其中：

3 基于矩阵的粒度约简算法

由定理5 的（1）（3）可以导出计算乐观多粒度粗糙集的粒度约简的算法，即算法1.

由定理5 的（2）（4），可以导出计算悲观多粒度粗糙集的粒度约简的算法，即算法2.

Step 2 计算COREP，时间复杂度为O(|D||AT|2|U|)；Step 4 计算REDP，时间复杂度为O(|D||AT|2|U|)；Step 6 计算REDP中是否存在可约粒度，时间复杂度为O(|D||AT|2|U|).

4 UCI 数据实验

4.1 时间效率为了验证两算法的时间效率，本文选取六个UCI 数据集（表1）来验证本文所提算法的有效性，样本数从178 到1055，属性数目从20 到41.所有实验均在系统为64-bit Windows 10 Inter（R） Core（TM） i7 6700HQ CPU @2.60 GHz 16 GB 的内存个人计算机上进行.所使用的编程语言是Matlab r2015b.

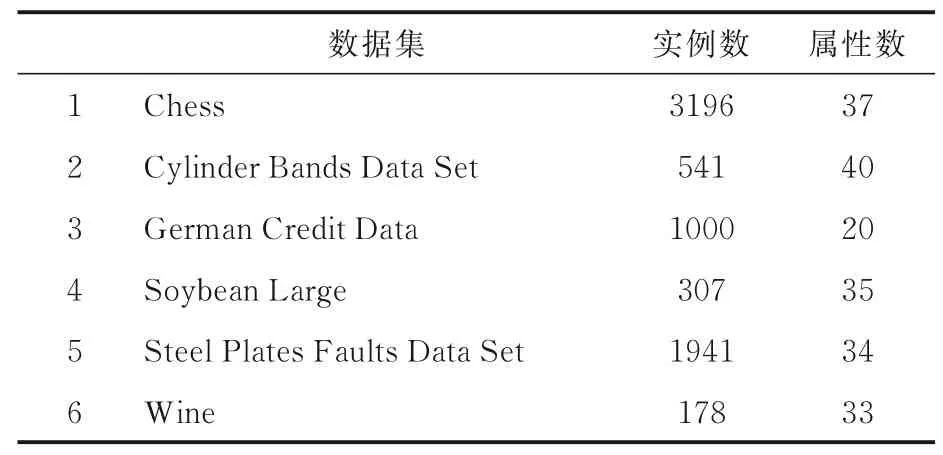
表1 实验使用的UCI 数据集Table 1 Details of UCI datasests

选取文献［8，14］中介绍的计算多粒度粗糙集粒度约简的高效算法（EAGRMRS）与悲观多粒度粗糙集中的粒度约简算法（GRAMGRS）作为对比算法，与本文的两个算法（OMBGRA，PMBGRA）进行对比.首先在同一数据集上模拟数据量增大的情况，将数据集大致等分为10 份，每次取出一份并入临时数据集并在临时数据集上进行10 次重复实验，记录计算粒度约简所需的时间，所得的结果如图1 所示.可以看出，本文的算法与对比算法相比，至少有一个数量级的时间优势.数据集增大时两种算法的计算时间均随数据集增大而增加，图1 所示的结果符合预期，本文的粒度约简算法更高效.而后在同数据集上模拟粒增大的情况，使粒逐渐增大，进行10 次重复实验，记录计算粒度约简所需要的时间，所得的结果如图2所示.可以看出，本文算法在同等粒度下比对比算法更高效.粒度增大时，两种算法的计算时间均随粒度增大而减少，这是因为每个粒度包含的属性更多时，粒度总数就变少了，图2 所示的结果符合预期.从图1 和图2 还可以发现，本文的两种算法在计算时间效率上差别不大，可以计入误差，这是因为计算粒度重要度的两种矩阵计算方法本身的复杂度并无差异，实验所得结果符合预期.

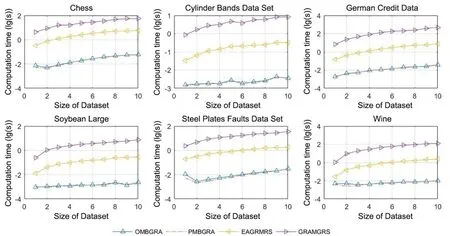
图1 数据集增大时四个算法的计算时间对比Fig.1 Time consumption of OMBGRA，PMBGRA，EAGRMRS and GRAMGRS with different size of datasets

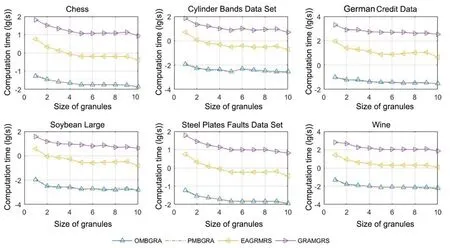
图2 粒度的属性集增大时四个算法的计算时间对比Fig.2 Time consumption of OMBGRA，PMBGRA，EAGRMRS and GRAMGRS with different size of granules

4.2 分类质量为了验证所提算法约简的质量，使用以下方式：使用每个数据集的每个单一粒度与决策一起构造一个数据集，在该构造数据集上取80%数据为训练集，余下的20%为测试集，在训练集上分别训练KNN（K 近邻分类器）［16］、CART（决策树CART 算法）［17］以及SVM（支持向量机）［18］，对测试集进行分类，将约简后的所有粒度构造的数据集上生成的分类结果取众数，计算分类精度（AC），所得结果如表2 所示.

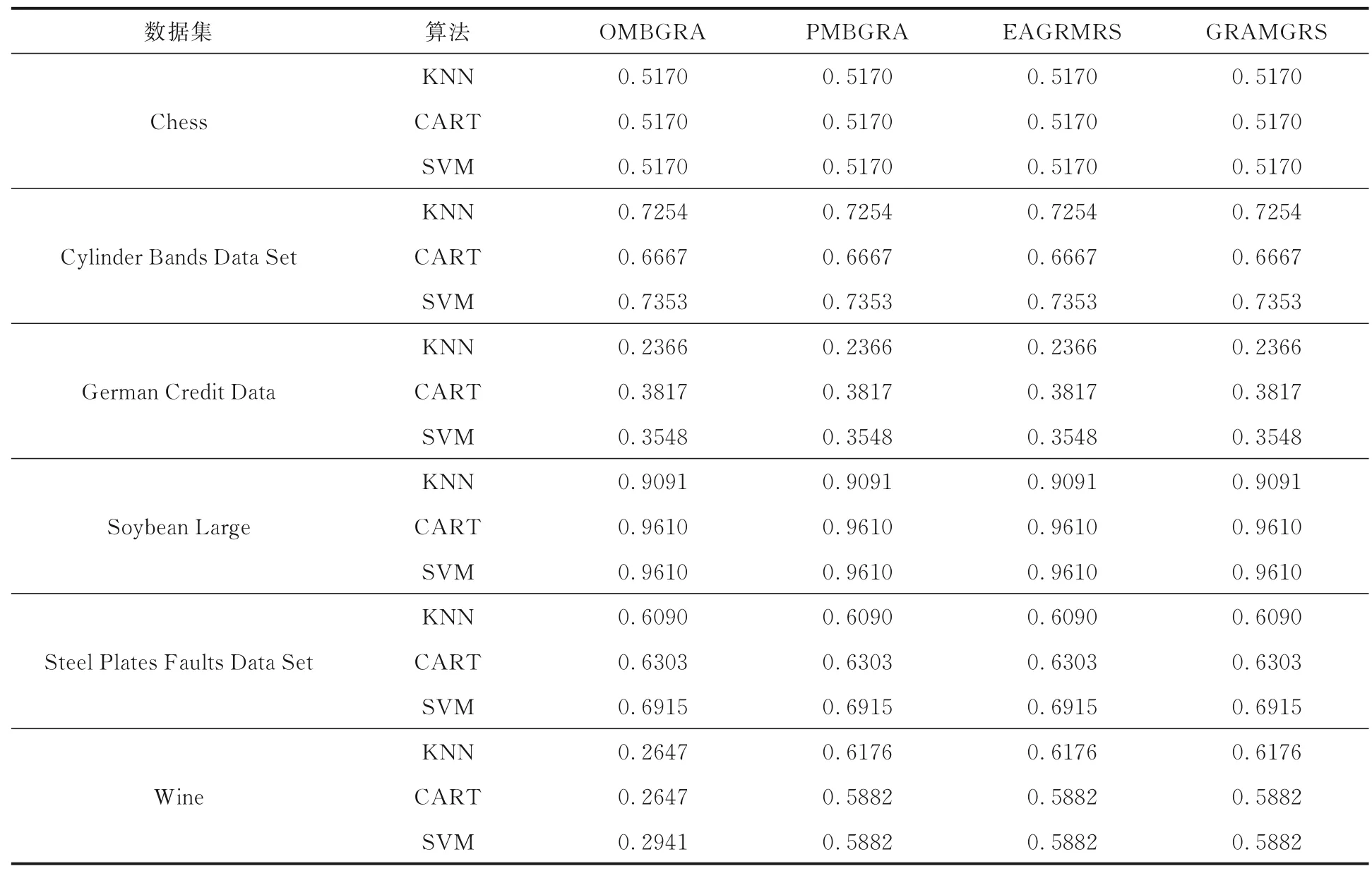
表2 不同算法的约简质量对比Table 2 The reduction quantities of different algorithms

可以看出，在多数投票的分类集成原则上，本文的约简算法生成的粒度约简所训练的分类器，在五个数据集上具有与对比算法一致的分类精度，其中PMBGRA 在所有数据集上都具有与对比算法一致的分类精度，可以在节省大量计算时间的基础上仍能够保证一定的分类精度.

5 结论

本文提出两种基于矩阵的多粒度粗糙集粒度约简方法，设计了相应的基于矩阵的粒度约简算法，进行了数据实验，验证了本文两种算法的有效性.与现存的粒度约简方法进行对比，本文的算法比对比算法的计算时间更短.因此，本文提出的计算方法及算法是可行且高效的.

经过约简的粒度可以使多粒度决策算法更加高效，并且在一定程度上提高决策算法的鲁棒性，在未来的研究中，将把所提出的粒度约简算法应用于设计高效的多粒度决策算法.