再努尔·木塔力甫，吴黎军

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐830046)

0 引言

信度理论是非寿险精算学的核心内容之一, 是非寿险中的一组经验评估技术. 信度模型包括古典信度模型和最精确信度模型. 在古典信度模型中, 需要确定当历史索赔数据达到多大规模时, 才能够赋予完全的可信度,而这个数据规模被称作为完全可信度标准，如果经验数据达不到完全可信度标准就赋予部分可信度. 在实际操作中我们得到的索赔数据规模往往达不到完全可信度标准,因此研究部分可信度的计算方法具有重要的实际意义.自从信度理论提出以后,许多学者对信度理论进行了研究. B¨uhlmann[1]建立了无分布信度模型,得到了信度保费公式. B¨uhlmann 和Straub在无分布信度模型的基础上, 将其推广至自然权重的情形.Hachemeister[2]在利用B¨ulmann-Straub 信度模型对美国各州的汽车第三者责任险进行定价时, 注意到索赔数据在时间分量上由于通货膨胀的影响具有时间趋势效应, 因而提出用回归模型来刻画该时间效应, 并且建立了回归信度模型. 回归信度模型的刻画如下, 假设某一个风险合同对索赔X有下面的模型成立:

这里j=1,2···,t,X=(X1,···,Xt)′为索赔样本,Yj为已知的设计向量,而β(Θ)为未知不可观测的随机系数向量,εi(i=1,2,···,t) 为随机误差项,也是不可观测的,且满足E(εj|Θ)=0,则风险参数Θ 给定时有E(Xj|Θ)=Yjβ(Θ).

经典信度理论中, 用平方损失函数来刻画保费与风险的拟合程度. 然而, 在20 世纪70 年代前后, 学者们注意到正误差与负误差引起的损失并不相同,他们认为某些情况对对称损失函数下所得出的估计会出现较高误差,于是非对称损失函数逐步得到重视. Zellner[3]提出了一种新的衡量参数估计优良性的标准, 从模型拟合度和估计的精度两个方面来综合衡量估计的好坏, 所考虑的损失函数为

作为Zellner 平衡损失函数的推广, 如下形式的平衡损失函数Lρ,ω,δ0(θ,δ)=ωρ(δ0,δ)+(1−ω)ρ(θ,δ)受到了很多关注,这里δ0是θ的预想目标估计,它可以是θ的极大似然估计或者最小二乘估计或者无偏估计等. 在精算学的领域,G´omez-D´eniz[4]则讨论了经典的B¨uhlmann 信度模型在平衡损失函数下信度保费及其性质. 国内学者[5−10]用平衡损失函数研究了信度估计模型. 本文将用平衡损失函数得出单份保单净保费的信度回归估计表达式.

1 预备知识及假设

设Θ 为未知的风险参数,X′=(X1,X2,···,Xt)为某保单在t年的观测数据. 本文估计的是, 当风险Θ 给定时,Xj的条件期望为µj(Θ), 这里µj(Θ)=E(Xj|Θ)是风险参数Θ 下保单在第j年的净保费,j=1,2,···,t. 考虑到通货膨胀, 回归假设中净保费µj(Θ)随时间发生变化, 且

Yj为(q×1)设计矩阵,β(Θ)为未知(q×1) 随机向量. 通过选择合适的设计矩阵Yj,可以刻画时间对净保费的影响.比如,若Yj是(2×1)矩阵且则µj(Θ)=β1(Θ)+jβ2(Θ)(j=1,2,···,t), β(Θ)=(β1(Θ),β2(Θ))′.若Yj=则µj(Θ)=β1(Θ)+jβ2(Θ)+j2β3(Θ)(j=1,2,···,t),β(Θ)=(β1(Θ),β2(Θ),β3(Θ))′. 下面介绍本文假设.

假设1设

假设2设矩阵Λ=Λ(q,q)=Cov[β(Θ)],Φ=Φ(t,t)=E[Cov(X|Θ)] 是正定矩阵(Λ 是回归系数向量β(Θ)的协方差, Φ 是Θ 给定时观测数据X的条件协方差的期望).

本文根据已知观测X′=(X1,X2,···,Xt)得出净保费µj(Θ)在平衡损失函数下的估计的表达式.

2 平衡损失函数下的净保费回归信度估计

首先给出线性代数中满足特殊条件的矩阵的求逆公式.

引理1设矩阵A 是(r×s)矩阵, B 是(s×r)矩阵且(I+AB)−1存在, 那么有如下求逆公式：

其中:I表示(r×r)单位矩阵.

证明 线性代数中的求逆公式(A+BCD)−1=A−1−A−1B(C−1+DA−1B)−1DA−1,取A=D=I,B=A,C=B就可得出以上公式.

信度保费用样本的线性函数预测未来保费, 使得期望平方损失函数达到最小, 求解下面的最优化问题:

下面的引理可以更方便地求信度估计, 其证明可参考文献[11].

引理2设随机向量的期望与协方差矩阵分别为

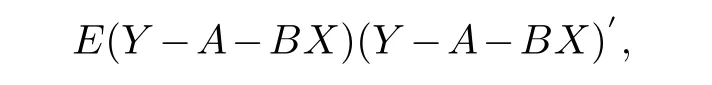
在矩阵的非负定意义下达到最小.

根据引理, 基于随机向量X的非齐次函数类的随机向量Y的最优预测为

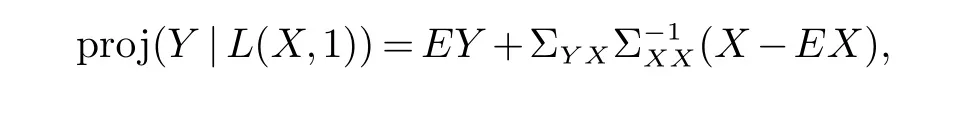
其中:proj(Y|L(X,1))表示Y在X的线性函数空间的正交投影.取损失函数为平衡损失函数:

其中:δ(µj(Θ))是µj(Θ) 的已知目标估计. 平衡损失函数下估计净保费等价于求解下面的最优化问题：

关于平衡损失函数下的信度理论有下面的引理3.

引理3在平衡损失函数

下,µj(Θ)的非齐次信度估计为

其证明可参考文献[6].

下面给出µj(Θ)在平衡损失函数下的回归信度估计. 令其中δ(β(Θ))是β(Θ)的已知目标估计, 设E[δ(β(Θ))]=µδ,Cov[δ(β(Θ),β(Θ)]=∆, 则

定理1基于以上假设及引理, 在平衡损失函数下净保费µj(Θ)的估计如下:

其中

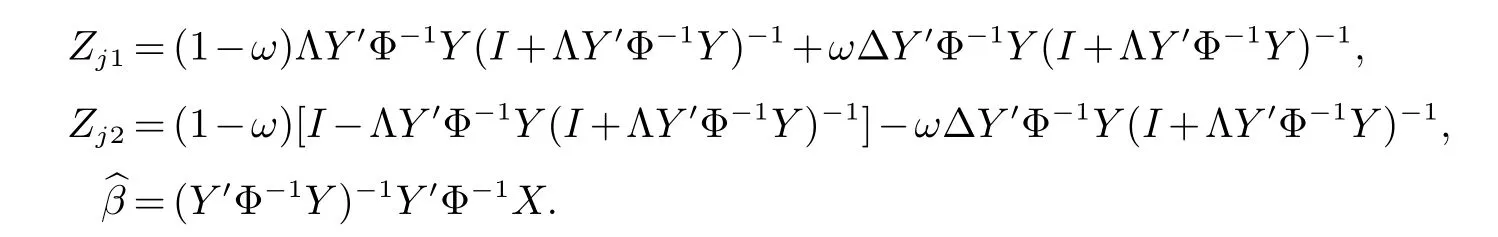
证明由假设1, 假设2可得由引理3 可得

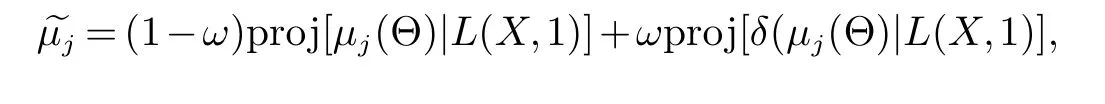
而根据引理1 和引理2 有

而

因此

定理得证.

3 结论

本文用投影公式和矩阵理论讨论了回归信度模型, 推出平衡损失函数下的净保费回归信度表达式, 推广了平方损失函数下的净保费回归信度模型. 本文中刻画了时间对净保费的影响, 用观测数据的线性函数估计了净保费, 推导过程中用到了求逆公式的特殊形式, 使得模型的推导更加简洁.