CHANG Lubin

(Electrical Engineering College,Naval University of Engineering,Wuhan 430033,China)

Abstract: The attitude estimation problem has been investigated making use of the concept of matrix Lie group.Through formulation of the attitude and gyroscope bias as elements of SE(3),the corresponding extended Kalman filter,termed asSE(3)-EKF,has been derived.It is shown that the resulting SE(3)-EKF is just the newly-derived geometric extended Kalman filter (GEKF) for spacecraft attitude estimation.This provides a new perspective on the GEKF besides the common frame errors definition.The simulation test shows that the proposed SE(3)-EKF performs quite similar with GEKF and can both outperform the traditional multiplicative EKF with large initial misalignment.In this respect,theSE(3)-EKF can relax the requirement of initial attitude accuracy for the linearized model approximation.

Key words: attitude estimation； extended Kalman filter； matrix Lie group； special Euclidean group.

Attitude estimation using vector observations has drawn much attention since the 1960s.For this problem,two facts have been widely approved,that is,gyroscopes are used in “dynamic model replacement mode”[1]and the utility of employing quaternions for attitude parameterization is preferred[2].For the first fact,since the gyroscopes have been used,the gyroscope bias is always estimated coupled with the attitude.For the second fact,many filtering methods have been devoted to handling the constraints inherent to non-minimal attitude representation.The extended Kalman filter (EKF) in multiplicative form (MEKF) is the workhorse for on-board attitude estimation due to its flexibility and computational efficiency[2,3].However,the EKF may prone to divergence when dynamics or measurement models are highly nonlinear,or there is no good a priori state estimate.In this case,some advanced nonlinear filtering algorithms can be applied[4-8].For more details about the advanced attitude estimators until 2006,the comprehensive and excellent survey paper [3] can be referred.It should be noted that most of these previous attitude estimators put much effort on the attitude part of the state vector.Non-attitude state vectors have still been handled in the general vector-space.From the perspective of matrix Lie group,these attitude estimators can be viewed as the extensions of general filters on special orthogonal group,i.e.SO （3）.

In recent few years,a filter called geometric extended Kalman filter (GEKF) has been well studied for attitude estimation[9-12].It has been demonstrated that the GEKF can outperform the MEKF.The main concept of GEKF is a new state-error definition with involved errors expressed in a common frame.The common frame is established making use of the estimated attitude error in each filtering recursion.Compared with the traditional state-error in vector-space,the frame consistent errors are more representative of the real errors experienced by the system.The frame consistent error is nonlinear due to error-attitude coupling with the states.In contrast with the linear error in vectorspace,such nonlinear error can be viewed as on manifold[13-18].The above viewpoint motives us to revisit the GEKF making use of the concept of Lie group whose operations are just performed on manifold.In this paper,we formulate the attitude matrix and gyroscope bias as elements of special Euclidean groupSE(3),a representative of the Lie group.The detailed filtering equations are derived making use of matrix Lie group and Lie algebra theories for attitude estimation.The resulting attitude estimation algorithm is termed as SE （3）-EKF.It is revealed that the GEKF with body frame attitude error bears much resemblance to,and thus can be viewed as,a kind of the SE （3）-EKF.This provides another perspective on the GEKF besides the common frame errors definition.

The organization of this paper proceeds as follows.In Section 2,the matrix Lie group and spacecraft attitude estimation model using vector observations have been introduced as mathematical preliminaries.In Section 3,the SE （3） -EKFwith body frame attitude error is derived.Its relationship with GEKF is also revealed and discussed.Simulation test is carried out in Section 4,which further validates the equivalence between SE （3）-EKFand GEKF.Some conclusions are drawn in the final section.

1 Mathematical preliminaries

In this section,the mathematical preliminaries related with matrix Lie group,Lie algebra and spacecraft attitude estimation model are provided,which will be used to derive the SE （3）-EKFin the following sections.

1.1 Matrix lie groups and lie algebra

The special Euclidean groupSE(3),which is always used to represent the poses,is simply the set of valid transformation matrices as ref.[14,17]

where SO （3）is special orthogonal group,representing rotations.SE （3）and SO （3）are both types of matrix Lie group .The mapΨ is given by

The inverse of an element of SE （3）is given by

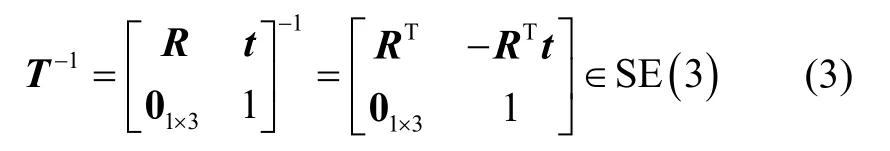
With every matrix Lie group is associated a Lie algebra.The Lie algebra associated with SE （3）is given by

where

The relation between a matrix Lie group to its associated Lie algebra is given by theexponential map.The elements of SE （3） are related to the elements of SE （3）through

where

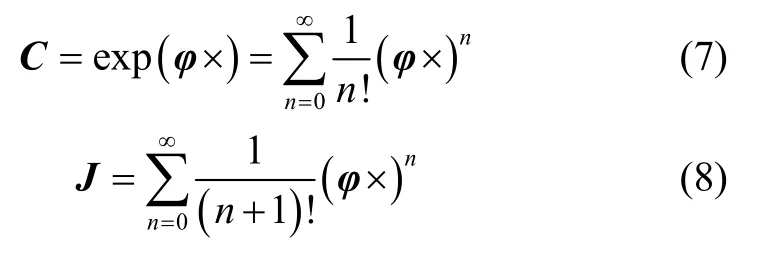
Letφ=φawhereφis the angle of rotation andis the unit-length axis of rotation.A direct series expression forTfrom the exponential map can also be obtained as

1.2 Attitude estimation model

Denote the attitude quaternion aswithbeing the vector component.The spacecraft attitude kinematics model in terms of quaternion is given by

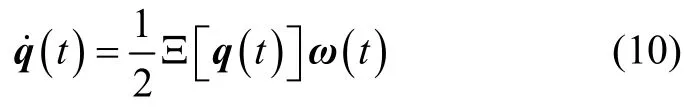
where

ωis the angular rate measured by the gyroscopes and governed by

whereβis the gyroscope bias which is assumed to be random walk.ηvandηuare assumed to be zero-mean,Gaussian white-noise processes.

The measurement model withnvector observations is given by

whereA(q)is the attitude matrix corresponding to quaternionq.υiis the measurement white noise for thei-th vector observation.

2 SE （3）-EKFwith body frame attitude error

In this paper,we follow the attitude error terminology in ref.[4,9] with emphases on the expressed frames of the attitude error.More specifically,given true quaternion related attitude matrixA(q)and its estimate,the body frame attitude error is given byand the reference attitude error is given by.This is a little difference with the terminology used in Lie group whereis termed asrighterror andas left error.Due to different representations of the attitude quaternion,the right attitude error may be expressed in reference frame[19].With the attitude error terminology in ref.[4,9],we will firstly derive the SE （3）-EKFwith body frame attitude error definition in this section.

Define the state asX=［A(q),β］.The transformation matrix corresponding to the state is given by

Assume the estimate ofχis.The estimation error is defined as

In the derivation of (15),the equation (3) has been used.It is clearly shown that the estimation error is also well-defined on the group SE （3）.According to relationship between matrix Lie group to its associated Lie algebra,γcan also be obtained as

wheredx∈R6.The linearized error dynamic model ofdxcan be given by

According to Eq.(9),a first order approximation ofγis given by

According to ref.[14],the first-order approximation of the error-attitude matrix is given by

whereδαhas components of roll,pitch and yaw error angles for any rotation sequence.

Substituting Eq.(19) into Eq.(15) yields

Comparing Eq.(18) and Eq.(20),the definite expression ofdxcan be obtained as

wheredαanddβis clearly defined in Eq.(21).

According to ref.[9],the explicit models ofδαandΔβare given by

Rewrite the definition ofdβas

Taking the time derivative of Eq.(24) gives

In Eq.(25),we have made use of the definitiondα=-δα.

Substituting Eq.(24) into Eq.(22) gives

According to the definitiondα=-δα,the model of the definitiondαcan be readily obtained as

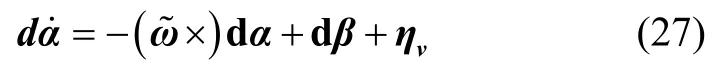
Based on Eq.(25) and Eq.(27),we can easily derive the Jacobians as

Next,we will derive the measurement transition matrix for the error-statedx.For a single sensor the true and estimated body vectors are given by

Subtracting Eq.(31) from Eq.(30) and making use of the approximation in (19) yield

Then,the linearized measurement model for multiple vector observations is given by

Given the above derived state-space model,the SE （3）-EKFfor spacecraft attitude estimation using vector observations is summarized in Algorithm 1.

Algorithm 1: SE （3）-EKF with Body Frame Attitude Error Initialize:Xˆ （t0）=■■A( qˆ (t0)),βˆ (t 0) ■ ■ =■■ A( qˆ0 ),βˆ0■■P （t0） = E（d x 0d x0T）Gain:Kk =Pk k -1H kT■■H k Pk k-1HkT+Rk■■-1 Update:dxˆk = K k （yk -h(Xˆk k -1)）χˆk =exp（dxˆk^）Ψ（Xˆk k-1）Recover Xˆkfrom χˆk Propagation:ωˆ （t） =ω˜ （t） -βˆ（t）q˙ˆ （t）= 12Ξ（qˆ （t）） ωˆ（t）χˆ （t） =Ψ （Xˆ(t)） =■■■ A （0 q1 ˆ×(3 t)） βˆ 1（t）■■■P˙ （t） =F （χˆ (t ),t） P （t） +P （t） F T （χˆ(t ),t）+G （χˆ (t ),t）Q k-1G （χˆ(t ),t）

In Algorithm 1,Hkandare given by

The transformation matrix estimate

is corresponding to the transformation matrix error definition in Eq.(15).If we divide the error-statedxas,according to the first order approximation of exponential map in Eq.(18),Eq.(36) can be further approximated as

If we let

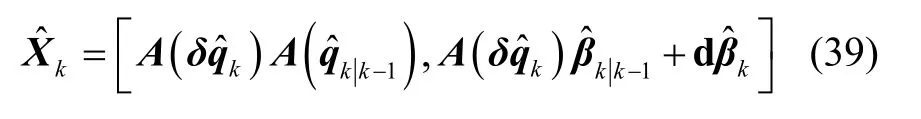
According to the aforementioned filtering recursion,if we useδαinstead ofdαto represent the attitude error,the resulting state-space model is identical with that of the GEKF.That is to say,the derived SE （3）-EKFwith body frame attitude error is just a minor variant of the multiplicative form of the GEKF (set aside the covariance update for the global state update).In other word,the GEKF for attitude estimation can be viewed as a kind of EKF on group SE （3） .This recognition provides another viewpoint on the geometric error-state used in GEKF.The common frame interpretation is virtually the physical meaning of the geometric error-state and the SE （3） based derivation can provide a mathematical perspective.

With the above perspective,the traditional MEKF can also be viewed as a kind of SO （3）-EKF.According to the invariance theory[13-18],SE （3） -EKF bears better invariance properties than SO （3） -EKF and therefore,can always outperform the SO （3）-EKF.This conclusion has been well demonstrated through the comparisons between traditional MEKF and GEKF in ref.[9].The main utility of the SE （3） perspective lies in the nonlinear state-error construction.When other parameters,such as gyroscope scale factors and misalignments,are added to the state vector,we can construct the corresponding nonlinear state-error according to the procedures Eq.(14) and Eq.(15).Actually,in practical applications,there may be no need to define all the involved parameters errors on manifold and some can be defined still in vector-space.For example,in ref.[20-22],the attitude-error coupled nonlinear velocity error has been used to improve the consistence of the inertial based integration.The concept used in ref.[20-22] can be viewed as formulating the attitude and velocity as elements of SE （3）.In this respect,we should firstly determine the group structure with the form SEn（3） ×R3×mwherenis the number of the three-dimensional parameters whose errors should be defined on manifold whilemis the number of those should be defined in vector-space.With the defined group structure,we can therefore determine the error-state and the corresponding state-space model.

It should be noted that there is no need to use Eq.(36) to update the state and the first-order approximation in Eq.(39) is adequate.This is because that when deriving the linear state-space model,first-order approximations Eq.(18) and Eq.(19) have been used.Rigorously updating state using Eq.(36) isn’t likely to add any additional accuracy.

3 Simulation Study

In this section,the SE （3）-EKFis evaluated using the spacecraft attitude estimation problem in ref.[6,23],by comparing with the two representative attitude estimators,i.e.MEKF and GEKF.In this problem,the spacecraft is in a 90-min low-Earth orbit and the body observations are derived from the star tracker.The star tracker can sense up to 10 stars in a 6 °× 6°field-of-view.The catalog contains stars that can be sensed up to a magnitude of 6.0 (larger magnitudes indicate dimmer stars).The number of available stars during simulation is shown in Fig.1.

Fig.1 Number of available stars

Firstly,the initial attitude estimate error is set as[1 1 1]°.The gyro bias is set to 0.1 °/ hfor each axis and the initial bias estimate is set to 0 for each axis.The initial covariance for the attitude error is set to (1 °)2for the three filters.The initial covariance for the attitude error is set to (0.1 °/h)2.The norm of the attitude estimate errors for the three filters is shown in Fig.2.The norm of the gyroscope bias estimate errors for the three filters is shown in Fig.3.It is shown that with small misalignment,the three filters perform identity with each other and there is no superiority of SE （3）-EKFand GEKF over traditional MEKF.That is to say,if the filter can be well initialized,there is no need to use the“advanced” filters.

Fig.2 Norm of attitude estimate errors with small misalignment

Fig.3 Norm of gyroscope bias estimate errors with small misalignment

Secondly,the initial attitude estimate error is set as[10 10 30]°.The gyro bias is set to 10 ° /hfor each axis and the initial bias estimate is set to 0 for each axis.The initial covariance for the attitude error is set to (15 °)2for the three filters.The initial covariance for the attitude error is set to (5 °/h)2.The norm of the attitude estimate errors for the three filters is shown in Fig.4.The norm of the gyroscope bias estimate errors for the three filters is shown in Fig.5.It is shown that with large initial misalignment,the superiority of SE （3）-EKFand GEKF over traditional MEKF can be observed.Meanwhile,the SE （3）-EKFperforms quite similar with GEKF.This can be understood easily because they are virtually equivalent.The slight difference is only caused by the involved random noise.

Fig.4 Norm of attitude estimate errors with large misalignment

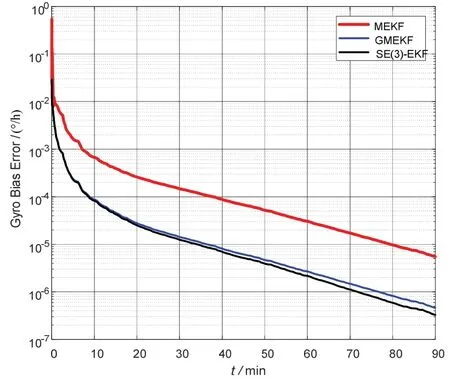
Fig.5 Norm of gyroscope bias estimate errors with large misalignment

From the above two simulation scenarios,the equivalence between SE （3）-EKFand GEKF can be further validated.Moreover,it can be concluded that the SE （3）-EKFand GEKF perform better than MEKF with large misalignment,which can relax the initialization requirement for the attitude estimators.

4 Conclusions

In this paper,the frame consistent error used in geometric extended Kalman filter has been re-derived using SE （3）formulation of the attitude matrix and gyroscope bias.In this respect,the geometric extended Kalman filter can be viewed as a type of SE （3）based extended Kalman filter for attitude estimation.In the further,the geometric extended Kalman filter will be further investigated making use of the invariance theory based on the SE （3）perspective.Meanwhile,the SE （3） perspective on geometric extended Kalman filter will also be extended to applications in inertial navigation.