李泽鹏， 耿培伦, 陈祥恩

(1.兰州大学 信息科学与工程学院， 甘肃 兰州 730000; 2.西北师范大学 数学与统计学院, 甘肃 兰州 730070)

0 引 言

图的可区别染色是近年来图染色研究的热点问题，主要体现图的局部结构颜色集合之间的可区别性.图的点可区别正常边染色是Burris在其博士论文中首次提出的[1]，此后该问题也被称为强边染色[2].图G的点可区别正常边染色是指G的一个正常边染色，使得任意两个顶点的色集合不同.使得G有k-点可区别正常边染色的最小正整数k称为G的点可区别正常边色数，记为′v(G).

Zhang等[3]将任意两点可区别的条件放松为任意两个相邻顶点可区别，从而提出了邻点可区别正常边染色的概念(也称为邻强边染色).图G的邻点可区别边色数是指对G进行邻点可区别边染色所需要的最小色数，记为′a(G).通过分析一些特殊图类，如树、圈、完全二部图和完全图等的邻点可区别正常边色数，学者们提出了下面的猜想.

猜想1对任意连通图G(|V(G)|≥6), 有

′a(G)≤Δ(G)+2.

对于更一般的情况，张忠辅等[4]在2006年提出了图的距离不大于r的任意两点可区别的正常边染色，即D(r)-点可区别正常边染色.显然，当r=1时，图G的D(r)-点可区别正常边染色，即G的邻点可区别正常边染色；当r≥d(G)时，图G的D(r)-点可区别正常边染色，即G的点可区别正常边染色，其中，d(G)是图G的直径.并且，对任意正整数r，有：

引理1设G是阶数至少为3的连通图，则

′a(G)≤′r(G)≤′v(G).

特别地，文献[4]得到了一些特殊图类，如圈、扇、轮、完全图、完全二部图、树以及一些联图的D(2)-点可区别边色数，并提出了如下猜想：

猜想2当r≥2时，对任意图G有

μr(G)≤′r(G)≤μr(G)+1，

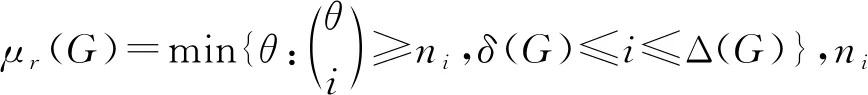
注意，图的D(r)-点可区别边染色也称为r-强边染色，此概念是Akbari等[5]独立提出的.

然而，猜想2被Kemnitz等[6]于2014年否定了.他们发现了一类圈Cp，满足D(2)-点可区别边色数′2(Cp)=μ2(Cp)+2，其中，

虽然猜想2被否定了，但是确定图的D(r)-点可区别边色数上界的问题仍是很有意义的工作.Tian等[8]利用概率方法得到了图的D(r)-点可区别边色数一个上界.

猜想3对任意正整数r≥2，存在常数δ0和C，使得对任意不含孤立边且最小度δ(G)≥δ0的图G，有

′r(G)≤Δ(G)+C.

刘利群等[10]确定了路与圈的Mycielski图的D(2)-点可区别边色数.关于图的D(r)-点可区别边染色详细的研究参见文献[11].

关于树的D(r)-点可区别边染色，Akbari等[5]证明了：对任意树T, 有′2(T)≤Δ(T)+1，且当T的任意两个最大度顶点之间的距离大于等于3时，′2(T)=Δ(T)；对最大度Δ(T)≥3的树T, 有′3(T)≤2Δ(T)-1.

1 预备知识

本文所涉及的图均为简单无向图.设G=(V(G),E(G))是一个图，其中V(G)和E(G)分别表示G的顶点集和边集.对顶点v∈V(G)，用d(v)表示v在G中的度数，N(v)表示v的所有邻点构成的集合.由于G是简单图，故d(v)=|N(v)|.若d(v)=1，则称v为G的叶子.用N1(v)表示v的邻点中所有叶子构成的集合.图G的最大度和最小度分别记为Δ(G)和δ(G).对顶点u,v∈V(G)，用d(u,v)表示u和v之间的距离，即u到v最短路的长度.图G的直径是指G中两个顶点之间的最大距离，记为diam(G)，即

diam(G)=max{d(u,v):u,v∈V(G)}.

图G的一个正常边染色是指对G的每条边分配一种颜色,使得任意相邻的两条边的颜色不同.设f是图G的一个正常边染色，v∈V(G)，记

C′(v)={f(vw):vw∈E(G)}，

称C′(v)为顶点v在边染色f下的色集合.

定义1[4]设f:V(G)→{1,2,…,k}是图G的一个正常边染色，如果对G中任意两个距离不超过r的顶点u,v∈V(G)，有C′(u)≠C′(v)，则称f为G的D(r)-点可区别边染色.图G的D(r)-点可区别边色数是指对图G进行D(r)-点可区别边染色所需要的最小色数，记为′r(G)，即

′r(G)=min{k:G有D(r)-点可区别边染色}.

图G的一个正常全染色f是指对G的每个顶点以及每条边分配一种颜色使得：

(1)对任意uv,vw∈E(G)，u≠w，有f(uv)≠f(vw);

(2)对任意uv∈E(G)，有f(u)≠f(v)，f(u)≠f(uv)，f(v)≠f(uv).

设f是G的一个正常全染色，v∈V(G)，记

C″(v)={f(v)}∪{f(vw):vw∈E(G)}，

称C″(v)为顶点v在全染色f下的色集合.

定义2[12-13]设f:V(G)∪E(G)→{1,2,…,k}是图G的一个正常全染色，如果对G中任意两个距离不超过r的顶点u,v∈V(G)，有C″(u)≠C″(v)，则称f为G的D(r)-点可区别全染色.图G的D(r)-点可区别全色数是指对图G进行D(r)-点可区别全染色所需要的最小色数，记为″r(G)，即″r(G)=min{k:G有D(r)-点可区别全染色}.

类似于邻点可区别边染色的概念，当r=1时，图G的D(r)-点可区别正常全染色即为G的邻点可区别正常全染色[14]，此问题已被广泛研究.

文中未给出的定义及符号，请参照图论文献[11,15].

2 树的D(r)-点可区别边染色

本节讨论树T的D(2)-点可区别边染色和D(3)-点可区别边染色，分别得到了对应的边染色的上界，并给出了线性时间的染色方案.

2.1 树的D(2)-点可区别边染色

Akbari等[5]证明了对任意树T有′2(T)≤Δ(T)+1成立，本小节给出了一种简单的证明方法.

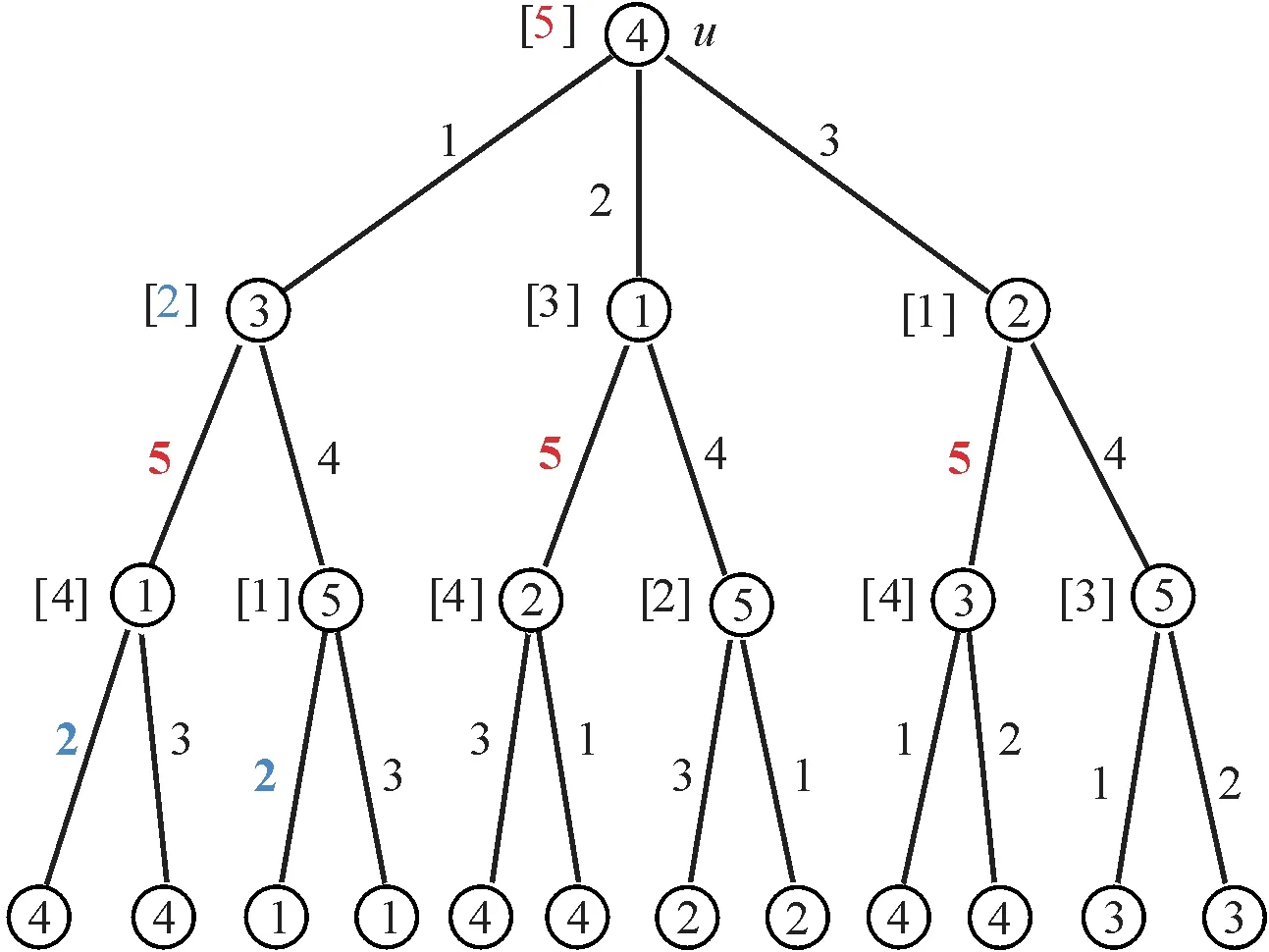
定理1对任意树T，可在线性时间给出T的一个使用了不超过Δ(T)+1种颜色的D(2)-点可区别边染色.

证明设总颜色集C={1,2,…,Δ(T)+1}，T的根节点为u.下面从树T的根u出发，逐层对T的边进行染色，并满足所有关联的边已染色的点是D(2)-点可区别的.

由于总颜色数为Δ(T)+1，因此,在染色之后每个顶点x的色集合C′(x)中至少有一种颜色没有出现.在下面染色中，笔者总是假定c(x)是C′(x)中未出现的一种颜色.

染色方案f如下：

对根节点u，令C′(u)={1,2,…,d(u)}，取c(u1),c(u2),…,c(ud(u))分别为f(uu2)、f(uu3)、…、f(uud(u))和f(uu1)，其中，u1,u2,…,ud(u)是u的子节点.

对其他任意节点x，设x的父节点为y，y的父节点为z(若存在)，且x是y的第m个子节点.令f(xx1)=c(y)，c(x)=f(yym+1)(当y≠u且m=d(y)-1时，c(x)=f(yz))，并令f(xx2),f(xx3), …,f(xxd(x)-1)为在C{c(x),f(xy),f(xx1)}中从大于f(xy)的第一个数开始顺序循环所取的d(x)-2种颜色.由于总颜色数为Δ(T)+1，所以|C{c(x),f(xy),f(xx1)}|≥d(x)-2.

易验证上述染色过程是线性时间的.下面证明此染色方案f是T的D(2)-点可区别边染色.因为只有度相同的顶点才可能有相同的色集，故下面讨论的顶点度均相等，且只讨论层数不低于x的节点，低于x的节点同理.

当x是T的叶子时，与x距离不超过2且是叶子的节点一定是y的邻点，根据上述染色规则可知，它们与x的颜色集不同，即与x是可区别的.下面考虑x不是T的叶子的情况.

(1) 与x距离为2的顶点包括z及y的除x外的子节点.

因为c(x)=f(yym+1)≠f(yy1)=c(z)，所以x与z的色集合不同.对y的除x外的任意子节点yt，因为c(x)≠c(yt)，且f(xy)≠f(yyt)，结合每个节点关联边上顺序染色的规则可知C′(x)≠C′(yt).

(2) 与x距离为1的顶点只有y.因为f(xx1)=c(y)，即C′(x)包含C′(y)缺少的颜色，故x与y的色集合是不同的.

□

2.2 树的D(3)-点可区别边染色

当T是星或双星时，即T中至多有两个顶点度数大于等于2，其余顶点的度数都是1时，diam(T)≤3，即T中任意两个顶点之间的距离都不超过3，因此，′3(T)=|E(T)|.

设T是一棵根为t的树，v是T中的任一顶点.用d1(v)表示v的邻点中叶子的数目.

定理2设T是一棵根为t的树，diam(T) ≥4，且t是T的叶子.令

h=max{d1(x)+d1(y)+2|x,y∈V(G)}，

则T存在使用了不超过max{Δ(T)+2,h}种颜色的D(3)-点可区别边染色.

证明设k=max{Δ(T)+2,h}，且使用的总颜色集C={1,2,…,k}.下面从树T的根t出发，逐层对T的边进行染色，并满足所有关联的边已染色的点是D(3)-点可区别的.

由于k=max{Δ(T)+2,h}≥Δ(T)+2，因此,在染色之后每个顶点x的色集合C′(x)中至少有两种颜色没有出现.在下面染色中，笔者总是假定c1(x)和c2(x)是C′(x)中未出现的两种颜色.

染色方案f如下：

(1)对根顶点t，设其唯一邻点为u,并令f(tu)=1. 取c1(t)=d(u)，c2(t)=d(u)+1.

(2)设u的孩子节点分别为u1,u2,…,ud(u)-1，令f(uui)=i+1，i=1,2,…,d(u)-1(图1). 并且，令c1(u)=d(u)+1，c2(u)=d(u)+2.

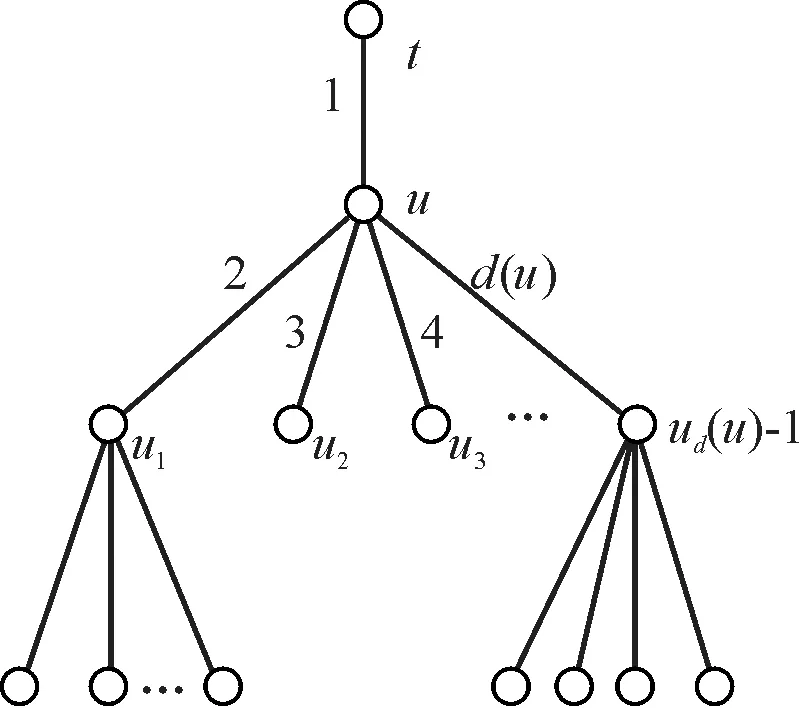
图1 顶点u的关联边的染色方案Fig.1 The coloring of the incident edges of u

(3)从u的孩子节点开始，逐层对u的子孙节点关联的未染色边进行染色.

对任意顶点x，设x的父节点为y，y的父节点为z，且x是y的第m个孩子，x的子节点分别为x1,x2,…xd(x)-1. 假设T中顶点y所在层及以上的顶点所关联的边均已经染好颜色，如图2所示.下面对顶点x关联的未染色边进行染色.用S(y)表示顶点y的关联边中一个端点是叶子的边的颜色集合，即S(y)={f(yw):w∈N1(y)}.显然，S(y)中的颜色在x关联的悬挂边上是不能出现的.

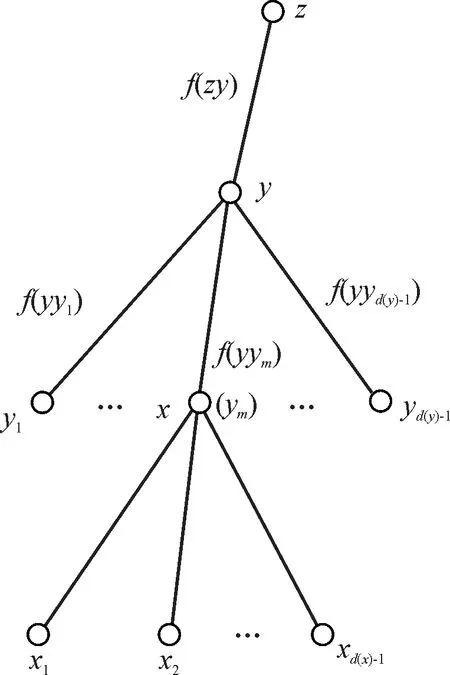
图2 树T的结构和染色Fig.2 The structure and coloring of the tree T

若x的子节点都是叶子且d1(y)+d1(x)=k-2，则c1(x),c2(x)待定.若y=u,y的子节点中除x外都是叶子，且d1(y)+d1(x)=k-2, 则c1(x),c2(x)待定.

对其余情况，都令c1(x)=c2(y)，c2(x)=f(yym+1)，当x=yd(y)-1时，令c2(x)=f(zy).

以下对与x关联的未染色边进行染色.

R1 若x的子节点中或y的子节点中没有叶子，则令{f(xx1)}={c1(z),c2(z)}∩{c1(y),c2(y)}，f(xx2),f(xx3),…,f(xxd(x)-1)分别为在C{c1(x),c2(x)}中从大于f(xy)的数开始顺序取d(x)-2个颜色，若颜色取尽则回到集合中的第一个颜色.

R2 若x和y的子节点中都存在叶子，但x的子节点不都是叶子或d1(y)+d1(x)

R3 若x和y的子节点中都存在叶子，x的子节点都是叶子且d1(y)+d1(x)=k-2，则f(xx1),f(xx2),…,f(xxd(x)-1)分别为在CS(y)中从大于f(xy)的数开始顺序取d(x)-1个颜色.

下面证明此染色方案f是T的D(3)-点可区别边染色.因为只有度相同的顶点才可能拥有相同的色集，故下面讨论的顶点度均相等，且只讨论层数不低于x的顶点，低于x的顶点同理.设z的父节点为w(若存在).

若x的子节点都是叶子，或者y=u且y的子节点中除x外都是叶子，且d1(y)+d1(x)=k-2，则f(xy)=c1(z)=c2(w)，故x与z和w一定可区别.另外，对z的任意子节点zi，由于c1(y)=c1(zi)=c2(z)，但由染色规则R3可知，C′(x)包含颜色c1(y)，故x与zi是可区别的.

若x是T的叶子，则与x距离不超过3且是叶子的节点一定是y或z的邻点，根据染色规则R2和R3可知，它们与x的颜色集不同，即与x是可区别的.下面考虑x不是T的叶子的情况.

(1)与x距离为3的顶点包括w及z的除y外的子节点.

由上述染色规则可知，c2(w)=c1(z)=f(yy1), 因此，c2(w)∉{c1(x),c2(x)}，此时，若f(xy)≠f(wp)，其中p是w的父节点，则根据每个节点关联边上顺序染色的规则可知,C′(x)≠C′(w)；若f(xy)=f(wp)，则根据c1(x),c2(x)的选取可知，c2(x)=f(yym+1)，但节点w关联边上是顺序染色的，因此，也有C′(x)≠C′(w).

设zi是z的除y外的任意子节点.由染色规则R1可知f(xx1)=c1(y)=c2(z)，而c1(zi)=c2(z)，因此，f(xx1)=c1(zi). 这说明f(xx1)∈C′(x)，但f(xx1)∉C(zi). 所以，C′(x)≠C′(zi).

(2)与x距离为2的顶点包括z及y的除x外的子节点.由染色规则R1可知f(xx1)=c2(z)，即有f(xx1)∈C′(x)，但f(xx1)∉C′(z)， 所以C′(x)≠C′(z).

对y的除x外的任意子节点yt，因为c2(x)≠c2(yt)，且f(xy)≠f(yyt)，结合每个节点关联边上顺序染色的规则可知C′(x)≠C′(yt).

(3)与x距离为1的顶点只有y.因为c2(x)=c1(y)，c1(x)≠c2(y)，且f(xy)≠f(yz)，所以C′(x)≠C′(y).

综上可知，f是T的D(3)-点可区别边染色，即有′3(T)≤max{Δ(T)+2,h}.

□

由定理2的证明过程可知下面结论成立.

推论1对任意树T，diam(T)≥4，可在线性时间给出T的使用不超过max{Δ(T)+2,h}种颜色的D(3)-点可区别边染色.

推论2设T是一棵树，diam(T)≥4，且h=max{d1(x)+d1(y)+2|x,y∈V(G)}≤Δ(T)+2, 则′3(T)≤Δ(T)+2.

3 树的D(r)-点可区别全染色

本节在树的D(2)-和D(3)-点可区别边染色基础上，进一步讨论树的D(2)-和D(3)-点可区别全染色.

定理3对任意树T，可在线性时间给出T的一个使用了不超过Δ(T)+3种颜色的D(2)-点可区别全染色.

证明对T中的边采用定理3中的染色方案对其进行染色，可得到T的一个使用了不超过Δ(T)+1种颜色的D(2)-点可区别边染色.然后对T的顶点用两种新颜色进行正常点染色，则所得到的染色f是T的D(2)-点可区别全染色.

□

事实上，通过定理3的证明过程得到的染色f也是T的D(3)-点可区别全染色.因为T中任意两个距离为3的顶点的点颜色是不同的，故它们的色集合也是不同的.所以，定理4成立.

定理4对任意树T，可在线性时间给出T的一个使用了不超过Δ(T)+3种颜色的D(3)-点可区别全染色.

□

另外，可通过定理2来证明定理4，具体证明过程如下：

对任意给定的树T，不妨设其顶点数大于等于3，给T的每个顶点上增加一条新的悬挂边，所得到的图仍是一棵树，记为T*. 即有：

V(T*)=V(T)∪{v*:∀v∈V(T)},

E(T*)=E(T)∪{vv*:∀v∈V(T)}.

显然，有Δ(T*)=Δ(T)+1，且

max{d1(x)+d1(y)+2|x,y∈V(T*)}=

2<Δ(T*)+2,

利用定理2的证明过程和推论2可知，在线性时间可得到T*的一个使用了不超过Δ(T*)+2种颜色的D(3)-点可区别边染色f*.下面在f*的基础上定义T的全染色f如下：

(1)对任意顶点v∈V(T)，令f(v)=f*(vv*)；

(2)对任意边uv∈E(T)，令f(uv)=f*(uv)；

由于f*是T*的D(3)-点可区别边染色，因此,对T中任意两个相邻的顶点u和v，边uu*和vv*在f*下的颜色是不同的，由f的定义可知，f(u)≠f(v),所以，f是T的一个正常全染色.另外，根据f与f*的关系可知，对T中任意顶点x，有C″(x)=C′(x)，所以f是T的D(3)-点可区别全染色.

□

下面，对定理3的结论进行改进，可得到树T的一个使用了不超过Δ(T)+2种颜色的D(2)-点可区别全染色.

定理5设T是一棵树，则

″2(T)≤Δ(T)+2.

证明当Δ(T)≤2时，易验证″2(T)≤4.

下面考虑Δ(T)≥3的情况.设使用的总颜色集C={1,2,…,Δ(T)+2}，树T的根节点是u，且d(u)=Δ(T). 下面从树T的根u出发，逐层对T的点和边进行染色，并满足所有关联的边和点本身已染色的顶点是D(2)-点可区别的.

由于总颜色数为Δ(T)+2，因此,在染色之后每个顶点x的色集合Cii(x)中至少有一种颜色没有出现.在以下染色中，笔者总是假定c(x)是Cii(x)中未出现的颜色.

染色方案f如下：

对根节点u，令C″(u)={1,2,…,d(u)}，f(u)=d(u)+1,取c(u1),c(u2),…,c(ud(u))分别为f(uu2),f(uu3),…,f(uud(u)),f(uu1)，其中,u1,u2, …,ud(u)是u的子节点.

对其他任意节点x，设x的父节点为y，y的父节点为z，x的子节点分别为x1,x2,…xd(x)-1，并且x是y的第m个子节点.

如果x是T的叶子，则只对顶点x进行染色即可.此时，令f(x)=c(y).

如果x不是T的叶子，则：

(1)令f(xx1)=c(y)，c(x)=f(yym+1)(当x≠ud(u)且m=d(y)-1时，令c(x)=f(yz))；

(2)取f(x)∈C{f(y),f(xy),f(xx1),c(x)}；

(3)令f(xx2),f(xx3),…,f(xxd(x)-1)为在C{c(x),f(x),f(xy),f(xx1)}中从大于f(xy)的第一个数开始顺序循环所取的d(x)-2种颜色，如图3所示(图中[p]表示该顶点缺少的颜色为p).

图3 一棵最大度为3的树的D(2)-点可区别全染色

由于|C{c(x),f(x),f(xy),f(xx1)}|≥Δ(T)+2 -4≥d(x)-2，故上述染色方案(3)是有效的.

下面证明此染色方案f是T的D(2)-点可区别全染色.只证明任意顶点x与其祖先顶点是可区别的.

当x是T的叶子时，与x距离不超过2且是叶子的节点一定是y的邻点，根据上述染色规则可知，y的所有关联边的颜色是不同的，但y的所有叶子邻点的颜色都是c(y)，因此,x与y的其他叶子邻点的色集合是不同的.下面考虑x不是T的叶子的情况.

(1)与x距离为2的顶点包括z及y的除x外的子节点.

因为f(xy)=c(z)，即C″(x)包含C″(z)缺少的颜色，所以x与z的色集合是不同的.对y的除x外的任意子节点yt，因为c(x)≠c(yt)，且f(xy)≠f(yyt)，所以，结合每个节点关联边上顺序染色的规则可知，C″(x)≠C″(yt).

(2)与x距离为1的顶点只有y.因为f(xx1)=c(y)，即C″(x)包含C″(y)缺少的颜色，故x与y的色集合是不同的.

综上所述，f是T的D(2)-点可区别全染色，因此，″2(T)≤Δ(T)+2.

□

4 结 论

本文对树的D(2)-点可区别边(全)染色和D(3)-点可区别边(全)染色进行了讨论，分别得到染色数的上界，并给出了线性时间的染色方案.

树的D(r)-点可区别边色数主要受到距离不超过r的叶子顶点数目的影响.特别地，当r比较大时，影响更为明显.

对任意k≥4，Akbari等[5]构造了树T，满足

′k-vd(T)≥Δ(T)(Δ(T)-1)|k/2|-1，

其构造如下：令u是T的根，让T中与u的距离小于|k/2|的顶点的度数均为Δ(T)，与u的距离等于|k/2|的顶点的度数均为1. 可以看出，T中包含Δ(T)(Δ(T)-1)|k/2|-1个度为1的顶点，且任意两个的距离不超过k，因此，′k-vd(T)≥Δ(T)(Δ(T)-1)|k/2|-1.

但树的D(r)-点可区别全色数受到距离不超过r的叶子顶点数目的影响较小，因为在全染色下每个顶点都有颜色，从而增加了备选的色集合.

对图G, 令

其中，ni表示度为i且任意两点间的距离不超过β的顶点的最大数目.

易验证，ηr(G)是图G具有D(r)-点可区别全染色所需颜色数的一个下界，即″r(G)≥ηr(G).

张忠辅等[12-13]猜想对任意图G有

ηr(G)≤′r(G)≤ηr(G)+1，