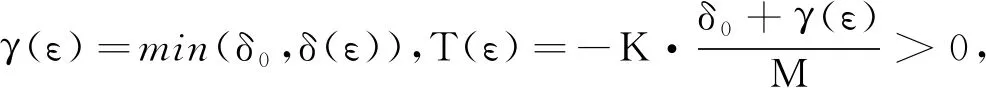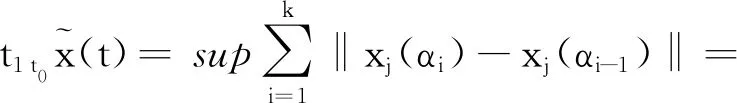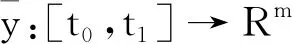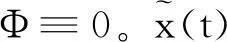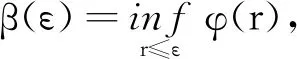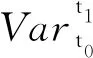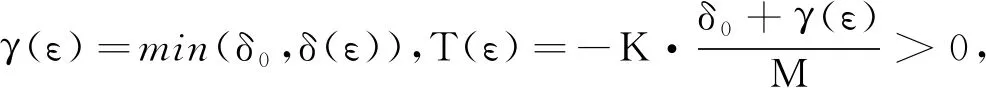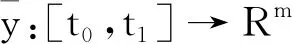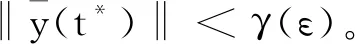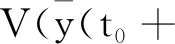李宝麟,王 宁

(西北师范大学数学与统计学院,甘肃 兰州 730070)

考察常微分方程

x=(x1,x2,…,xn)T,

考虑Carathéodory方程

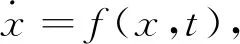
(1)

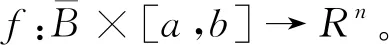
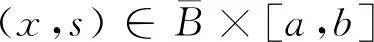
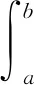
成立。

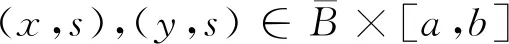
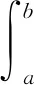
‖f(x,s)-f(y,s)‖≤l(s)ω(‖x-y‖)

成立。

Carathéodory方程是一类不连续系统,在适当的条件下等价于广义常微分方程。文献[2]利用李雅普诺夫函数讨论了广义常微分方程的稳定性理论。

1 预备知识

研究介绍Kurzweil积分与广义常微分方程的概念以及研究要用到的一些已有结果。

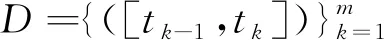
定义1函数U:[a,b]×[a,b]→Rn在区间[a,b]称为Kurzweil可积的,如果存在向量I∈Rn,使得对任意的ε>0,存在正值函数δ(t):[a,b]→(0,+∞),使得对区间[a,b]的任何δ-精细分划D:a=α0<α1<…<αk=b有[2]

定义2如果函数F:G→Rn∈F(G,h,ω),G=Bc×[0,+∞)。对任意的t1,t2∈[0,+∞)有

F(0,t2)-F(0,t1)=0,

即对任意的s1,s2∈[0,+∞)有[2]

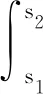
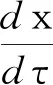
(2)

定义5若Carathéodory方程(1)的平凡解y≡0既是变差稳定的又是变差吸引的,则称Carathéodory方程(1)的平凡解y≡0是渐近变差稳定的。

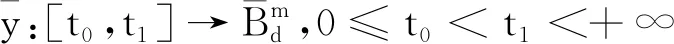
当‖x(t0)‖<δ,

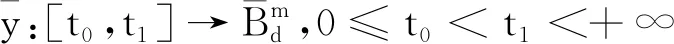
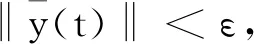
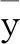
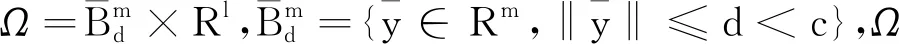
2 主要结论

研究主要讨论了Carathéodory方程(1)的变差稳定性和渐近变差稳定性。

(ⅰ) 存在一个连续递增实函数b:[0,+∞)→R,使得b(ρ)=0当且仅ρ=0。

V(x,t)≥b(‖x‖),

(3)

V(0,t)=0,

(4)

并且(ⅲ)成立。

|V(x,t)-V(y,t)|≤K‖x-y‖。

(5)

如果函数V(x(t),t)对Carathéodory方程(1)的任何一个解y(t)是非增函数,则方程(1)的平凡解y≡0是变差稳定的。

证明令

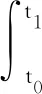
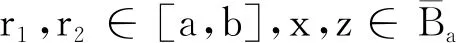
‖F(x,r2)-F(x,r1)‖=

‖F(x,r2)-F(x,r1)-F(z,r2)+F(z,r1)‖=

ω(‖x-z‖)|h2(r2)-h2(r1)|,

再证Carathéodory方程(1)的平凡解x≡0是变差稳定的。

由于假设函数V(x(t),t)对Carathéodory方程(1)的任何一个解x:[α,β]→Rn是非增函数,即对广义常微分方程(2)的任何一个解x:[α,β]→Rn也成立,所以对t∈[α,β]有

下述证明在这种假设下定义3的条件是满足的。给定ε>0,令y:[t0,t1]→Rn是区间[t0,t1]上的有界变差函数,且在(t0,t1]上左连续。由于函数V满足文献[2]中引理10.12的(10.16)和(10.17)式,其中:取Φ≡0。结合式(4)和式(5)可知,|V(0,t0)-V(y(t0),t0)|≤K‖y(t0)‖,所以对任意的r∈[t0,t1]有

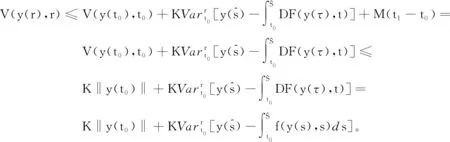
(6)

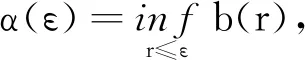
则由式(6)可得

V(y(r),r)≤K‖y(t0)‖+Kδ(ε)≤2Kδ(ε)<α(ε),r∈[t0,t1]

(7)

如果存在一个ξ∈[t0,t1],使得‖y(ξ)‖≥ε,则由式(3)可得

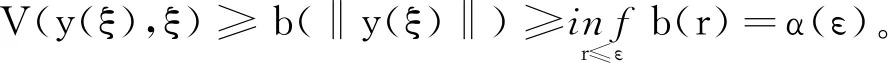
这与式(7)矛盾。因此对所有的t∈[t0,t1],‖y(t)‖<ε成立,即证得Carathéodory方程(1)的平凡解x≡0是变差稳定的。

-Φ(x(t))

(8)

成立,其中Φ:Rn→R是连续的,且Φ(0)=0,当x≠0时,Φ(x)>0。则Carathéodory方程(1)的平凡解x≡0是渐近变差稳定的。

证明由式(8)可得,函数V(x(t),t)对Carathéodory方程(1)的任何一个解x:[α,β]→Rn是非增函数。因此,由定理1可得Carathéodory方程(1)的平凡解x≡0是变差稳定的。根据定义5,以下只需证明其解是变差吸引的即可。

由Carathéodory方程(1)的平凡解x≡0是变差稳定的可知,存在一个δ0∈(0,a),如果y:[t0,t1]→Rn,0≤t0

对任意的ε>0,由Carathéodory方程(1)的平凡解x≡0的稳定性可知,存在一个δ(ε)>0,使得对任意的y:[t0,t1]→Rn,0≤t0

则对t∈[t0,t1]有

‖y(t)‖<ε。

(9)

M=sup{-Φ(x):γ(ε)≤‖x‖<ε}=

-inf{Φ(x):γ(ε)≤‖x‖<ε}<0。

假设y:[t0,t1]→Rn在区间[t0,t1]上是有界变差函数,且在(t0,t1]上是左连续的,使得‖y(t0)‖<δ0,且

令T(ε)

V(y(t0+T(ε),t0+T(ε)))-V(y(t0),t0)≤

因此

V(y(t0+T(ε),t0+T(ε)))≤V(y(t0),t0)-Kδ0≤

K‖y(t0)‖-Kδ0

这与不等式

V(y(t0+T(ε),t0+T(ε)))≥b(‖y(t0+

T(ε))‖)≥b(γ(ε))>0

矛盾。所以一定存在一个t*∈[t0,t0+T(ε)],使得‖y(t*)‖<γ(ε)。又结合式(9),对所有的t∈[t*,t1],有‖y(t)‖<ε。因此对t>t0+T(ε)也有‖y(t)‖<ε,所以Carathéodory方程(1)的解x≡0是变差吸引的,即证得Carathéodory方程(1)的解x≡0是渐近变差稳定的。

定理3设函数V:Ω×[0,+∞)→R,使得对任意x∈Ω,函数V(x,·)左连续,假设V(x,·)是正定的,既满足以下条件(ⅰ)(ⅱ):

(ⅰ) 存在一个连续递增的实函数φ:[0,+∞)→R,使得φ(ρ)=0当且仅ρ=0。

(10)

V(0,t)=0,

(11)

并且(ⅲ)成立。

(ⅲ) 对任意的x,x′∈Ω,常数K>0有

|V(x,t)-V(x′,t)|≤K‖x-x′‖。

(12)

由于假设函数V(x(t),t)对Carathéodory方程(1)的任何一个解x:[α,β]→Rn是非增函数,即对广义常微分方程(4)的任意一个解x:[α,β]→Rn也成立,所以对t∈[α,β]有

对[t0,t1]上的任何一个分划D:t0=α1<α2<…<αk=t1,有

(13)

V(x(r),r)≤V(x(t0),t0)+

(14)

因此,当

‖x(t0)‖<δ(ε),

则由式(14)可得

V(x(r),r)≤K‖x(t0)‖+Kδ(ε)≤2Kδ(ε)<

β(ε)，r∈[t0,t1]

(15)

定理4设函数V:Ω×[0,+∞)→R,满足和定理3一样的性质,如果对Carathéodory方程(1)的任何一个解x:[t0,t1]→Ω,当t∈[t0,t1]时,

-Φ(x(t))

(16)

对任意的ε>0,由 Carathéodory方程(1)的平凡解x≡0的变差稳定性可知,存在一个δ(ε)>0,使得对任意的y:[t2,t3]→Rm,0≤t2

则对所有t∈[t2,t3],有‖y(t)‖<ε。

M=sup{-Φ(x):γ(ε)≤‖x‖<ε}=

-inf{Φ(x):γ(ε)≤‖x‖<ε}<0。

(17)

V(x(t0+T(ε),t0+T(ε)))-V(x(t0),t0)≤

MT(ε)

因此

V(x(t0+T(ε),t0+T(ε)))≤V(x(t0),t0)-Kδ0≤

K‖x(t0)‖-Kδ0

这与不等式

T(ε))‖)≥φ(γ(ε))>0