彭勇　陈俞强

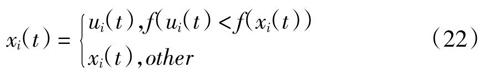
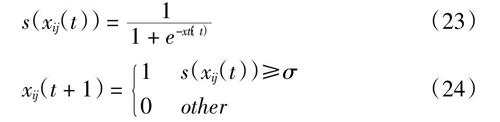
摘   要：随着高校实验课程比例越来越高，针对传统实验室排课手段效率低、出现冲突的可能性高等缺点，提出了一种基于改进布谷鸟算法的智能排课模型。首先，定义了课元表示教师在什么班级上什么课程，把排课问题转化为课元确定教室-时间对，提出了一个多目标、多约束的排课数学模型。其次将数学模型的求解转化为对二部图进行完美匹配操作获取初始解。然后，利用差分进化方法改进了布谷鸟算法，实现布谷鸟算法在实验室排课中的应用。最后，通過对仿真实验的结果分析来验证算法可行性与有效性。

关键词：实验室排课;布谷鸟算法;二部图;差分进化;课元;排课模型

中图分类号：TP319                                             文献标识码：A

Application of Improved Cuckoo Search Based on Differential Evolution

in Laboratory Course Arrangement

PENG Yong？覮，CHEN Yu-qiang

（Department of Computer，Dongguan Polytechnic College，Dongguan，Guangdong 523808，China）

Abstract：As proportion of experimental courses is increasing in colleges，aiming at the shortcomings of low efficiency and high possibility of conflict in traditional laboratory course arrangement methods，an intelligent course scheduling model based on improved cuckoo algorithm is proposed. Firstly，it defines the course elements to indicate what classes and courses teachers are taking，transforming the problem of course scheduling into course elements to determine classroom-time pairs，a mathematical model of multi-objective and multi-constraint is proposed. Secondly，the solution of mathematical model is transformed into perfect matching of bipartite graphs，then，the improved cuckoo search based on differential evolution is used to find the optimal schedule in the solution space，finally，the feasibility and validity of the algorithm are verified by analyzing the simulation results.

Key words：laboratory course arrangement;cuckoo search;bipartite graphs;differential evolution;course elements ;course scheduling model

在高校的实验室管理中，实验课程排课是一项非常复杂而繁琐的工作。近年来，高校招生规模日益扩大，各种新型专业课程层出不穷，大部分专业课程都要求在实验室进行理实一体化教学，尽管实验室建设进度也不断加快，但是实验实训资源仍然十分短缺，各高校对实验室的利用率提出较高的要求，尽量让课程能够共享实验室，这无形就增大了实训课程排课的复杂度和难度。目前高校排课很多还是利用Excel软件由教学秘书手工排课，远远不能满足新时代高校实验室排课的需求。早在70年代，高校排课问题就被证明是一个NP完全问题，即算法的计算时间是呈指数增长的，这一论断确立了排课问题的理论深度[1]。

近年来，有很多学者针对不同应用环境的高校排课问题给出不同的解决方法。苏军波提出运用在把排课过程转化为二部图之后，首先利用贪心选择最大未排课班级，再贪心选择符合课程要求的最小教室，降低了排课算法的复杂度，最终的算法的复杂度由指数复杂度降为线性复杂度[2]，但当问题规模较大时，贪心算法运算时间过长，得到的结果不是全局最优;蒋中云运用混合蚂蚁的信息素来改进蚁群算法解决了排课问题[3]，该算法与传统的蚁群算法对比，有所提升，但在排课的算法模型生还不够优化，与高校实际排课还是有一定差距;张媛探索了禁忌搜索法来设计排课系统，该系统可操作性强，搜索效率高，具有可用性与可适性[4]，该算法的把各种排课约束表示填充到禁忌表，较好的管理了约束，但对约束的不同等级没有分析，没有区分硬约束和软约束;高健、高培等人在传统模拟退火算法的基础上，通过加入一个记录因子来保留较好的状态，不会丢失每次迭代的最优解，同时还给出了一个可变步长的温度更新函数，并通过双阈值的设置减少了计算量，提高了模拟退火算法在求解排课问题上的可行性和有效性[5]，但由于排课算法的复杂度非常高，特别是达到一定规模的排课实际问题，上述算法无法得到较好的排课结果。

智能进化算法发展日新月异，各种新型智能进化算法层出不穷。例如蝙蝠算法、萤火虫算法、生物地理学算法等，其中布谷鸟搜索（Cuckoo Search，缩写 CS），是由YANG Xin-she和DEB S于2009年提出的一种新兴启发算法[6]，具有参数少、操作简单、易实现、随机搜索路径优和寻优能力强等优点，目前已经应用于电力系统、生物医药、模糊控制、金融、电子与电磁场等领域。本文提出一种基于差分进化的布谷鸟优化算法应用于实验室排课，旨在合理利用实训资源，提高排课的效率。

1   高校排课问题数学描述

排课问题是一个多元分配问题，主要包括教师、课程、班级、教室、时间这5个元组，但这5个元组不是随机分配的，一般而言，高校在每学期期末就确定了下学期每个老师的教学任务，即哪位教师承担某个班级的什么课程，这个是已经确定的，一般情况下并不能调整，我们把教师、课程和班级的组合定义为教学课程元（简称为课元），那么排课问题这个多元分配问题转变成在满足约束情况下为每个课元分配给教室和时间的问题[7]，这就成为一个三元问题了，在这个三元问题中，有两类排课约束，一类是必须满足的，如果不满足的话，完全无法上课，我们称为硬约束，比如两个班排到同一教室上不同的课程;还有一类我们称为软约束，主要是最好要满足，没有满足的话只是影响教学效果或老师的满意度，比如同一门课程最好是不要同一天或连续两天都安排。

1.1   变量表示

（1）课元集合M：课元表示教师、课程和班级的集合，具体如表1所示。

表1   课元示例

其中，M = {M1，M2，…，Mm}为所有课元构成的集合，按照班级c（·） = βs人数从大到小排列;函数h（·）用来提取课元Mi所任教的教师为αk;函数c（·）用来提取课元Mi所任教的班级为βs;Wi表示课元Mi对教室的要求，已经按要求的从低到高排序，这种需求主要和课程属性有关，有些课程操作性非常强，就需要普通机房;有的课程以讲解为主，就需求多媒体教室，但在机房上可也以，为了简化排课模型，对部分理论教学，部分上机实验的课程，我们统一以机房为准。教室要求的优先级顺序为W1：多媒体教室

（2）教室集合N：包含校区、教室编号、教室类别（例如多媒体教室、普通机房、多功能教室、图书馆报告厅）和可容纳人数（工位数），一共有n个教室，N = {N1，Nj，…，Nn}。

（3）上课时段集合T：定义的是教學时间段，一般情况下，教师按照大节（包含2节课）上课，一天的教学实践可以分为第一大节、第二大节、第三大节、第四大节和第五大节共计5个时间段，则每周共有25个授课时间元，T = {T1，Tt，…，T25}，例如T1表示周一第一大节（上午12节），T10表示周二第五大节（晚上9、10节）。

（4）教师集合H：则表1中h（Mi） = αk∈H，并记αk = （0 … 1 … 0）T为除第k行为 1 其余各行都是0的单位向量，向量的维度等于教师总数H。

（5）班级集合C：则表1中c（Mi） = βs∈C，并记 βs = （0 … 1 … 0）T为除第s行为 1 其余各行都是0的单位向量，向量维度等于班级总数C。

（6）根据以上表述，在实验室排课就是在满足上述条件的情况下，为每一个课元元素找出最佳的教室时间对，即在什么时候，某位老师带某个班级的什么课程在指定的教室上课。课元和教室时间对D之间共有2D个映射。

（1）

可以将课元Mi的排课结果Ri■N×T表示为教室和授课时间之间的有序元素对（Nj，Tt）构成的集合，排课决策变量为：

rijt = 1，Mi课元被按安排在Nj教室Tt时间段进行2个课时教学0，否则        （2）

排课结果：

Ri = （j，t）|rijt ≠ 0，i = 1，2，…，m          （3）

1.2   排课所遵循的约束条件

（1）硬约束条件

1）对教师的约束：在同一个上课时段内老师只能在一个班级上一门课。

■αkrijt = ■h（Mi）rijt ≤ 1          （4）

2）班级约束：在同一个上课时段一个班级内只能在一个教室上一门课。

■βsrijt = ■c（Mi）rijt ≤ 1          （5）

3）教室约束：在同一个上课时段内一个教室只能安排上一门课程。

■rijt ≤ 1          （6）

4）课时约束：课元Mi的每周的课时量为Xi，每次课记2个课时。

■2rijt = Xi          （7）

5）人数约束：课元Mi的班级人数必须小于实验室的工位数，Nj表示实验室工位数，c（Mj）表示班级人数。

（j，t）∈Ri，Nj≥c（Mj），i = 1，2，…，m

（8）

6）教室类型约束：教室N的类型标准必须大于课元Mi的教室要求Wi，函数L（·）用来提取教室的类型值。

（j，t）∈Ri，L（Nj）≥Wi，i = 1，2，…，m     （9）

（2）软约束条件

1）学习效果约束

排课时间段尽量安排在学习效果较好的时间段，即让学习效果：

f1 = max■p（Tt）rijt          （10）

尽可能大。

表2   时间段评价值

函数p（·）用来提取时间段Tt所对应的学习效果评估值，根据我们的问卷调查和随机访谈，对于绝大部分学生而言，在上午12节上课，取得的学习效果最好，其次是上午34节和下午78节，下午56节效果更差一些，晚上（9、10节）和周五的下午78节的学习效果最差，这个效果评价可以根据季节和学校实际情况进行调整。

2）排课间隔约束

相同课程的排课结果Ri在时间段T中尽可能分散，即方差：

f2 = max■■（j - ■）2          （11）

保持最大，实际上就是一门课程在同一个班不能连续排课，为了提高教学效果，让学生有自行消化吸收已经课程复习和预习时间，把课程适当排散。

3）可用资源约束

排课结果Ri应使未利用教室的座位总和：

f3 = max■Nj（1 - rijt）          （12）

尽可能大，也就是安排完所有课元后，还有最多的教室-时间对资源可以，以便部分老师出差时，调整课程方便。

综上所述，排课问题实际是一个整数线性约束的多目标优化模型，可以描述为如下：

max（C1 f1 + C2 f2 + C3 f3）        （13）

2   基于改进布谷鸟算法的高校排课

2.1   标准布谷鸟算法

根据文献[8]所述标准布谷鸟搜索算法，可知布谷鸟寻巢的位置更新公式如下：

xi（t + 1） = xi（t） + α ■ Levy（λ），i = 1，2，…，n

（14）

在第t + 1代时，第i个鸟巢的位置为xi（t + 1）;α是用于控制飞行距离的常数;■为点对点乘法; Levy（λ）表示搜索下一个鸟巢位置的路径，服从 Levy分布：

Levy（λ） ～ μ = t-λ（1 < λ ≤ 3）        （15）

随机莱维飞行的计算：

Levy（λ） ～ ■        （16）

其中，μ和ν都服从正态分布，φ的计算公式如下：

φ = ■■       （17）

为了能够更好地控制随机搜索的范围，采用如下公式计算α：

α = α0（xi（t） - xbest）        （18）

其中，α0为常数，xbest表示最优鸟巢位置。

综上所述，CS算法采用以下公式生成新的解：

xi（t + 1） = xi（t） - α0 ■（xi（t） - xbest）   （19）

具体的CS算法流程详见文献[9]。

CS算法通过增加迭代的时间，一般情况下是可以找到较优的解，但是由于对解的搜索完全依赖于Levy飞行这样一个随机游走的过程，CS算法的快速收敛性和高精度无法得到保证。

2.2   差分进化布谷鸟搜索算法思想

差分进化实际是一种增加通过差分策略增加种群多样性的一种全局优化算法，主要的差分手段有变异、交叉、选择，与遗传算法类似，但是算子的具体内容和遗传算法有较大差别，通过不同的差分操作促进种群中不同个体之间的竞争与合作，可以保留最优个体的有效遗传的基础上，通过个体信息交流，提高种群个体的多样性，是一种非常有效的全局优化算法[10]。

在CS算法基础上，第t代鸟巢并不是直接进入（ t + 1） 次迭代，而是对其进行变异、交叉、选择操作，通过变异，增加个体的差异性，通过交叉，增加整个种群的多样性，通过选择，能够指导个体进化的方向，提高快速收敛性，使个体向种群中优秀个体靠拢，得到新的鸟巢位置后，再进入（t+1）次迭代，然后回到标准布谷鸟算法进行莱维飞行搜索，更新鸟巢的位置[11，12]。

1）变异

xi（t）為第t代时，第i个鸟巢的位置，随机从种群中提取两个其他个体xr1（t）、xr2（t），利用式（20）产生变异个体vi（t）：

vi（t） = xi（t） + F（xr1（t） - xr2（t））        （20）

其中，F是变异因子，F ∈ [0，2]。 可以看出，vi（t）既包含了xi（t）部分信息，根据变异因子的大小，vi（t）还能够获得种群其他个体xr1（t）、xr2（t）的信息，实现种群个体间信息的交流？

2）交叉

交叉是对变异个体vi（t）和第t代个体xi（t）的重组：

uij（t）=vij（t），rand（0，1）≤CR or j = rand（1，n）xij（t），rand（0，1）>CR or j ≠ rand（1，n）

（21）

其中，CR∈ [0，1]是交叉概率，rand（0，1）是[0，1]区间均匀分布的随机数，rand[1，d]是[1，d]区间均匀分布的随机整数，j = 1，2，…，d。可以看出，候选个体uij（t）至少有一维的分量是由变异个体vi（t）贡献的，种群的多样性明显得到提升。

3）选择

通过适应度函数来判断第t代个体xi（t）与候选个体ui（t）之间的支配关系，产生（t+1）代个体xi（t+1），可以将较优的差异化的个体传承到下一代。

xi（t） = ui（t），f（ui（t） < f（xi（t））xi（t），other        （22）

2.3   布谷鸟算法的二进制转换

在标准的CS算法中，每次迭代解更新的位置是解空间中的连续值，多用于求解连续解空间的优化问题。为了使算法能处理搜索空间是离散值的情况，Rodrigues等[13]人提出了二进制布谷鸟算法（Binary Cuckoo Algorithm，BCS），BCS是布谷鸟算法的二进制版本。在 BCS中将每一个鸟巢编码为一个二进制值向量，每一个鸟巢表示一个候选解，每一个布谷鸟蛋表示一个特征，向量中数值1表示特征被选择，0表示特征没有被选择。

使用如下公式将鸟巢每个维度的值映射为二进制值：

s（xij（t）） = ■        （23）

xij（t + 1） = 1     s（xij（t））≥σ0     other        （24）

式中，函数s为一个Sigmond映射函数，可将 xij（t）映射到[0，1];i = 1，2，…，m（m为布谷鸟种群数）;j = 1，2，…，d（d 为编码长度）;σ为在[0，1]区间均匀分布的随机数;xij（t+1）表示t+1次迭代中第i个鸟巢的第j维的数值。

2.4   基于差分进化的多目标布谷鸟算法

多目标进化算法实际是得到一个全局最优的解集，在这个过程中需要保证每个解的Pareto前沿收敛性和多样性特征。对具有K个子目标的多目标优化问题，Yang等提出了一种多目标布谷鸟算法[14]，在结合上述差分进化思想后，其具体步骤如图1所示：

图1   基于差分进化的多目标布谷鸟算法流程图

2.5   解的构造

布谷鸟算法的编码好坏直接影响到算法的计算复杂度，令教师的课表作为每个鸟巢的编码，编码位数由排课规模决定，其结构示例如下：

表3   课元编码表

表4   鸟巢编码表

设有某位教师（教师编号为0011）承担2017级计算机应用技术专业1班（班级编号为1100）的《移动应用开发技术》课程（课程编号为0101），则可以得到其课元编号为001111000101，这个在每个学期末就已经确定，一般不再修改;该课元的一种排课计划为：教室为教三203（编号为11011），授课时间段为周四下午56节（编号为10010），则可以得到一个可行解的二进制编码为0011110001011101110010，（鸟巢的二进制表示）。

2.6   解的初始化

由上述的分析可知，排课问题就是将课元M向教室-时间对笛卡尔积D上映射，可用二部图的完美匹配算法来解决，所得的结果不一定是最优解，但是这个结果一定是满足基本约束条件的可行解[14]。

图2   排课问题二部图构造初始解模型

图3中左边集合M表示课元，即教师、课程和班级的集合，是由院系每学期期末下发的下学期教学任务，它是已知的，不可调整的;右边D表示教室-时间对，可根据公式（1）获得，即教室集合与授课时间段集合的笛卡尔积。集合M与D的笛卡尔积就是排课问题的解空间，可根据表3和表4对其进行二进制编码。通过二部图完美匹配算法求出一个包含M集合所有元素的M × D一个真子集，此真子集就是排课问题的初始解。

2.7   基于改進布谷鸟的多目标排课算法

3   仿真实验及结果分析

3.1   实验环境

软件环境：Windows 7 64位，Matlab 2016a;

硬件环境：CPU：Intel（R） i7-77003.60GHz;内存：8.00GB;硬盘：128G SSD+1TB。

3.2   参数设置

本文实验中参数设置如下：种群规模为150，迭代次数为200，淘汰概率pα = 0.25，变异因子F = 0.35，交叉概率 CR = 0.25，目标函数权值因子C1、C2、C3分别取0.4、0.3、0.3。

图3   基于改进布谷鸟的多目标排课算法

3.3   结果分析

（1）基于差分进化的多目标二进制布谷鸟算法（IMBCS）标准二进制布谷鸟算法（BCS）的性能比较

1）收敛性比较

object[1]

图4   BCS算法非支配前沿

object[1]

图5   IMBCS算法非支配前沿

从图5和图4中可以看出，IMBCS算法目标收敛形状较规则，IMBCS算法的收敛性稍好于BCS算法。

2）多样性比较

mean_rank_size，maximum generation=200

大小

mean_rank_size，maximum generation=200

图7   IMBCS算法1-3前沿平均大小

从图6与图7对比，可以看出，IMBCS算法的多样性明显好于BCS算法。BCS算法的第3前沿平均大小在130代左右就基本趋于零值，而由于采用了差分进化的模式，IMBCS算法无论第2还是第3前沿平均大小均未出现衰减为0的现象。由于在迭代初期就增加了种群的多样性，使其避免陷入局部最優而获得全局最优值，所以IMBCS算法在多样性明显强于BCS算法，说明本文的算法改进是成功的。

3）排课效果比较

表5   排课性能评估与对比表

从表5可得，IMBCS算法比起BCS算法在操作时间上略有增加，主要由于IMBCS算法增加了变异、交叉、选择计算，但由于采取多线程对IMBCS算法进行了加速，所以增加不多，但在排课质量指标（学习效果、排课间隔、剩余可用资源）上均较大优于BCS算法。

4   结  论

高校排课问题是一个多元分配问题，通过分析高校实验室排课实践中的各种变量，找出排课过程中需要遵循的软硬约束，将高校实验室排课问题转化为了一个整数线性约束的多目标优化模型，为解决排课问题提供了数学描述基础。在标准布谷鸟算法的基础上，通过Sigmond映射函数将连续布谷鸟算法改进为二进制布谷鸟算法，再通过差分进化的方法改善了算法的收敛性和多样性，利用二部图完美匹配算法构造初始种群，并用于对实验室排课模型的求解。通过具体的实验分析了不同算法求解模型的收敛性和求解结果质量，得出基于差分进化布谷鸟算法的所得结果令人满意，能明显提高排课工作效率。

参考文献

[1]    张媛，祁兰.高校实验室排课系统的研究与开发[J].榆林学院学报，2018，28（3）：97—99.

[2]    苏军波.基于优化的启发式算法进行排课的研究[D].长春：东北师范大学，2018.

[3]    蒋中云.基于改进蚁群算法的机房排课系统设计与实现[J].信息技术，2014，（2）：56—59.

[4]    张媛.基于禁忌搜索法的排课系统设计与应用[J].电子设计工程，2018，26（16）：40—44.

[5]    高健，廖斌华，高培.基于改进模拟退火算法的中学排课问题[J].工业控制计算机，2018，31（1）：101—102+104.

[6]    张宸瑞.布谷鸟算法的含分布式电源配电网最优潮流优化[J].现代电子技术，2017，40（15）：159—162.

[7]    李静，赵建平.高校排课系统优化模型的可行性研究[J].数学的实践与认识，2018，48（20）：234—243.

[8]    马卫，孙正兴，李俊楼. 基于Powell局部搜索策略的全局优化布谷鸟算法[J]. 计算机应用研究，2015，32（6）：1667—1675.

[9]    王凡，贺兴时，王燕. 基于高斯扰动的布谷鸟搜索算法[J]. 西安工程大学学报，2011，25（4）：566—569.

[10]  刘凤龙，陈曦，曹敦. 基于差分演化的K-均值聚类算法[J]. 计算技术与自动化. 2010，19（01）：48—50.

[11]  SU Gan-than. Multi-objective differential evolution with diversity enhancement[J]. Journal of Zhejiang University，2010，11（07）：538—543.

[12]  MEHTA P，BHATT P，PANDYA V. Optimized coordinated control of frequency and voltage for distributed generating system using Cuckoo Search Algorithm [J]. Ain Shams Engineering Journal，2018，9（4）：1855—1864.

[13]  崔妍，王权，王康，等. 排课问题的数学模型[J].沈阳工程学院学报：自然科学版，2016，12（3）：276—278+288.

[14]  YANG Xin-she，SUASH D. Multiobjective cuckoo search for design optimization[J]. Computer & Operations and Research，2013，40：1616—1624.