广东省佛山市乐从中学

一 题目与解答

题目(2019年高中数学联赛福建赛区预赛第12题)已知F为椭圆1的右焦点,点P为直线x=4 上动点,过点P作椭圆C的切线PA、PB,A、B为切点.

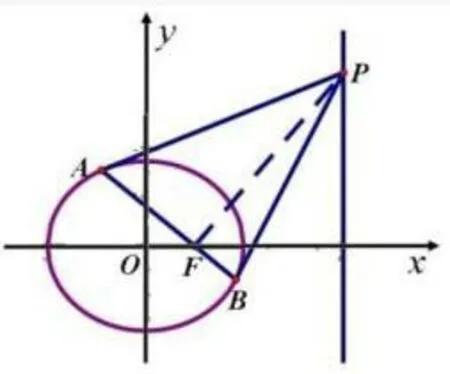
图1

(1)求证:A、F、B三点共线;

(2)求ΔPAB面积的最小值.

解答如图.(1)易得F(1,0),设P(4,t),A(x1,y1),B(x2,y2).则切线PA,PB的方程分别为由切线PA,PB过点P(4,t),得即由此可得直线AB方程为易知直线AB过点F(1,0).所以A、F、B三点共线.

评析问题(1)可直接用椭圆的切点弦方程求解.事实上,有如下结论:

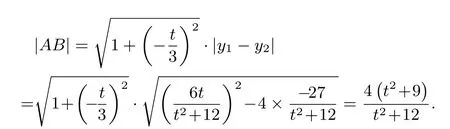
又点P(4,t)到直线AB的距离所以

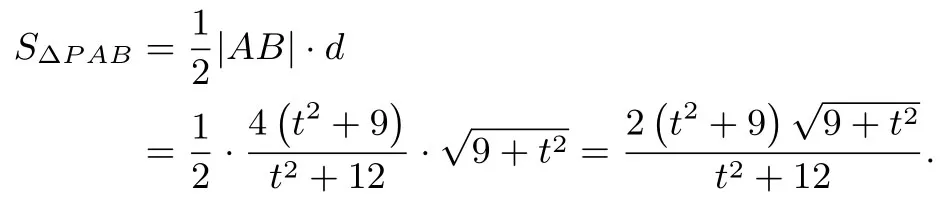
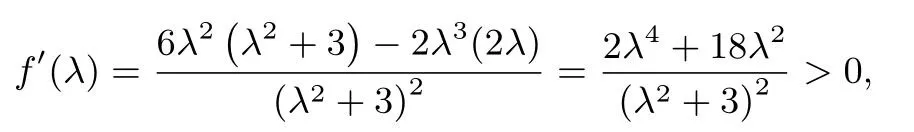
所以f(λ)在[3,+∞)上为增函数,f(λ)的最小值为f(3)=此时t=0.所以ΔPAB面积的最小值为

评析问题(2)的解法是官方答案,解法的运算量虽不小,但方法是解析几何中的常用方法,这种通性通法在数学解题中有重要作用.所以在平时的教学中要注重一般性的解题规律和方法(即通性通法),要重视知识的生成过程,尽量创设问题情境引导学生探究知识,培养学生分析问题、解决问题的能力.

二 问题的提出及一个引理

数学家波利亚曾说:“解题就象采蘑菇一样,当我们发现一个蘑菇时,它的周围可能有一个蘑菇圈.”解答完本题后,自然思考:

问题1竞赛题的问题(1)在一般的椭圆1(a>b>0)是否成立?

问题2若问题1 成立,则ΔPAB面积是否有最小值?如有,最小值是多少?

问题3在原竞赛题的条件下,还有没有其它性质?

由于后面结论的证明要用到一个引理及其推论,这里先行给出.

引理已知圆锥曲线(椭圆,双曲线,抛物线)的焦点F在x轴上,设倾斜角为α的直线l经过点F,且与圆锥曲线交于A,B两点,记圆锥曲线的离心率为e,则

推论1在椭圆中,因为所以

推论2在双曲线中,因为所以若A,B在双曲线同一支上,若A,B不在双曲线同一支上

推论3抛物线中,因为e=1,所以

上述引理及推论,利用圆锥曲线统一的极坐标方程较易证明,限于篇幅,在此不再给出其证明过程.

三 借题探索 结论推广

通过探索,可得如下结论:

结论1已知F(c,0)为椭圆的右焦点,点P为右准线上的动点,过点P作椭圆C的切线PA、PB,A、B为切点.

(1)A、F、B三点共线;

(2)PF⊥AB;

(3)ΔPAB面积的最小值为

证明(1)设因为PA、PB与椭圆相切,由椭圆的切点弦方程可知,直线AB的方程为易得点F(c,0)在直线AB上,所以A、F、B三点共线.

(2)当t=0时,直线AB的方程为x=c,故直线AB垂直于x轴,此时点P在x轴上,显然有PF⊥AB.

当t ̸=0时,直线AB不垂直于x轴,由直线AB的方程可知,直线AB的斜率为

而直线PF的斜率为所以

综上可得PF⊥AB.

(3)由(2)可知PF⊥AB,故ΔPAB的面积SΔBAB=

由图1,易知当点P在x轴上,|PF|最小,最小值为于是,当点P在x轴上,即此时弦AB垂直于x轴,|AB|与|PF|均为最小.所以,ΔPAB面积的最小值为

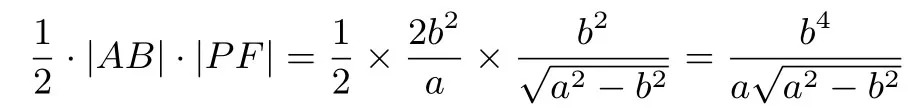
评析显然当a2=4b2=3时,可算得ΔPAB面积的最小值为,就是原竞赛题的情形.结论1(3)也可以用原竞赛题的解法,但是运算量极大,这里巧妙地利用PG⊥AB,及焦点弦的弦长公式,代数变形简单,运算量少,证法快捷,新颖.所以在竞赛层面,要重视方法的积累和知识的储备,熟练掌握一些有用的结论,才有可能缩短思维的长度,提高效率,达到事半功倍的效果.

四 探索延伸 类比性质

我们知道,双曲线,抛物线与椭圆都是圆锥曲线,很多时侯三者之间有可类比的性质,那么双曲线与抛物线是不是也有类似于结论1的性质呢? 经探索,得到如下结论:

结论2已知F(c,0)为双曲线0,b >0)的右焦点,点P为右准线上的动点,过点P作双曲线C的右支的切线PA、PB,A、B为切点.

(1)A、F、B三点共线;

(2)PF⊥AB;

(3)ΔPAB面积的最小值为

结论3已知F为抛物线C:y2=2px(p >0)的焦点,点P为准线上的动点,过点P作抛物线C的切线PA、PB,A、B为切点.

(1)A、F、B三点共线;

(2)PF⊥AB;

(3)ΔPAB面积的最小值为p2.

证明(1)设因为PA、PB与抛物线相切,由抛物线的切点弦方程可知,直线AB的方程为即易得点在直线AB上,所以A、F、B三点共线.

(2)当t=0时,直线AB的方程为故直线AB垂直于x轴,此时点P在x轴上,显然有PF⊥AB.当t ̸=0时,直线AB不垂直于x轴,由直线AB的方程可知,直线AB的斜率为而直线PF的斜率为所以综上可得PF⊥AB.

(3)由(2)可知PF⊥AB,故ΔPAB的面积SΔP AB=

五 问题探索的再思考

(1)由椭圆的对称性,将结论1的右焦点,右准线换成左焦点,左准线,结论不变.

(2)由双曲线的对称性,将结论2的右焦点,右准线换成左焦点,左准线,且两切点在双曲线的左支上,结论不变.

(3)结论3 中,将抛物线方程换成y2=-2px,结论不变.

(4)在结论2的条件中,若将两个切点在双曲线的右支上改为两个切点在分别在双曲线的两支上时,会有什么样的结论?

(5)在结论2的条件中,保持点P 在双曲线的右准线上,若将两个切点在双曲线的右支上改为两个切点在双曲线的左支上,又会有什么样的结论?

这些留给感兴趣的读者去探索了.

六 结束语

圆锥曲线具有很多相似的性质,这体现了圆锥曲线性质的内在统一的和谐美.这些优美的性质深刻反映了数学独特的无穷魅力,值得我们去寻找、发现和欣赏.数学家波利亚曾说过“一个有意义的题目的求解,为解此题所花的努力和由此得到的结论和见解,可以打开通向一门新的学科,甚至通向一个科学新纪元的门户”.学数学离不开解题,但不能仅仅局限于老师讲题、学生做题,而是要借助题目,探索隐藏在题目背后的奥秘,将研究的问题引向深入,挖掘题目的真正内涵,能够找到解决这个问题与解决其它问题在思维上的共性.这样我们才能领会到试题命制的深刻背景,才能引领学生跳出题海,真正做到触类旁通,举一反三,从而达到做一题会一类,甚至会一片的目的,最终让学生在解题思路上产生质的变化,使思维得到发展.

对题目的拓展、引申探究是一名数学教师必备的专业素养,平时要重视对典型问题的深入研究,探研规律,并适当拓展,充分挖掘题目的育人价值.高中数学新课程理念之一是倡导积极主动、勇于探索的学习方式,而学东西的最好方式是发现它,所以要鼓励学生通过合情推理对某些问题作大胆的猜想,并进行探索与证明,这样的探索在数学学习中起到重要作用.教师可根据学生实际,通过探究活动,让学生体验数学的发现和创造历程,引导他们勇于发现问题、提出问题、解决问题,进而让学生在分析、类比、猜想、证明过程中全面提高学生的综合能力,从而提升学生的数学核心素养.