几何中的动点问题之最值问题

2020-03-27

井冈教育 2020年1期

关键词：动点边长圆心

几何图形的知识一直是学生学习的难点，它的特点是空间想象力和抽象思维的能力体现，而动点问题就要求更高，本文拿几何动点最值计算问题为例来说明如何解决这类题型。为解决有关运动问题的最值计算，通常需用到两种基本模型和一个基本原理：

模型一点在直线上运动，如下图，点P 在直线l 上运动，则直线外定点A 与点P 的最小距离为AP 1 时AP 的长最小（即垂线段最短）；

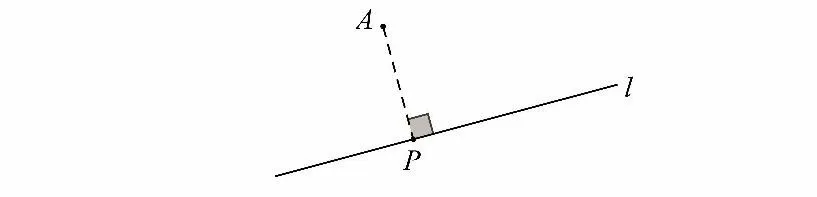
基本原理当点P 跟随另一点A 运动而运动时，我们把点A 叫作主动点，点P 叫作从动点.若主动点A 在某一直线l 上运动，则从动点P 也在直线上运动（可能是直线l 也可能是直线m）；若主动点A 在圆上运动，则从动点P 也在圆上运动。

掌握以上两个基本模型及原理，可以快速有效地解决有关运动为背景的最大（小）值问题。

例1 如图1-1，等边三角形ABC 的边长为4，点D 在AC 边上运动，以BD为斜边在BD 上方作含30°角的直角三角形BDE，连接AE，则AE 的最小值为_________。

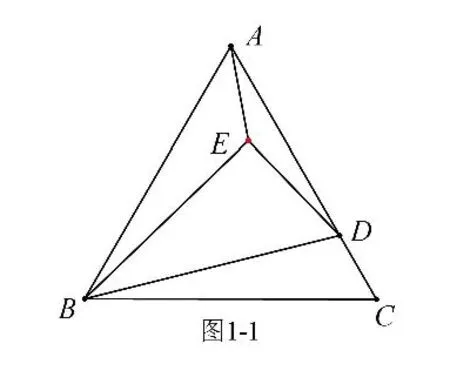
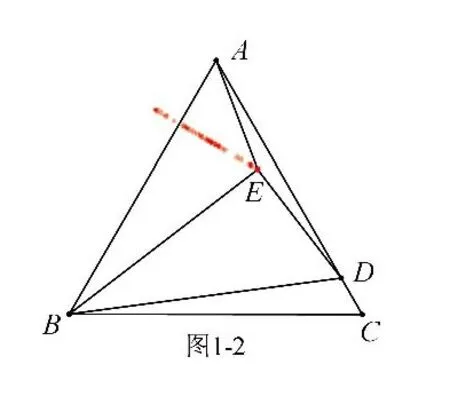
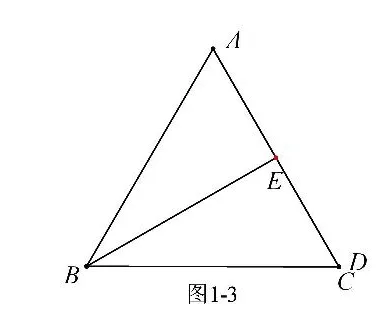
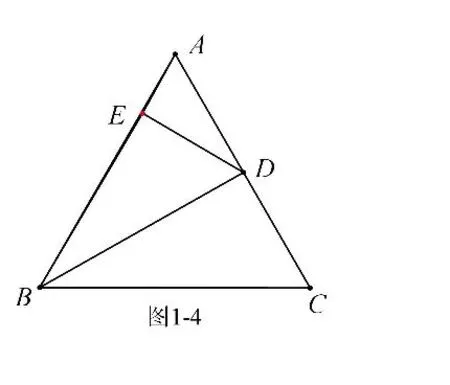
解析：①点E 随着点D 的运动而运动,点D 在AC 边上运动（在直线上运动），故点E 也在直线上运动，如图1-2；②AE 的最小值就是当AE 与直线垂直时的长，点E 运动轨迹（直线）在哪呢（如何确定）？应找两个特殊点来确定——当D 与C 重合时，E为AC 中点（如图1-3）；当D 在AC中点处时，E 在AB 上（如图1-4），所以点E 实际就是在图1-4 中的直线DE 上运动.显然在Rt

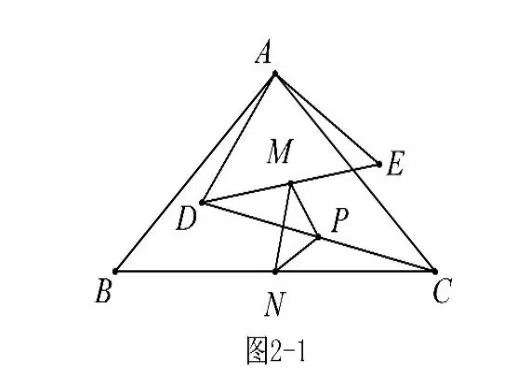
例2 （河南）如图2-1，在△ABC 与△ADE中，∠BAC=∠DAE=90°,AB=AC=10,AD=AE=4,把△DAE 绕着点A 在平面内自由旋转，在旋转过程中，M、P、N 始终分别为DE、CD、BC 的中点，求△PMN 面积的最大值和最小值。

解析：1、在△PMN 中，N是定点，P、M 随着△ADE 的旋转而运动，易证△PMN是等腰直角三角形，故△PMN 的面积===即△PMN 的面积随着边长的增大而增大；

2、如何求边长的最大值呢？

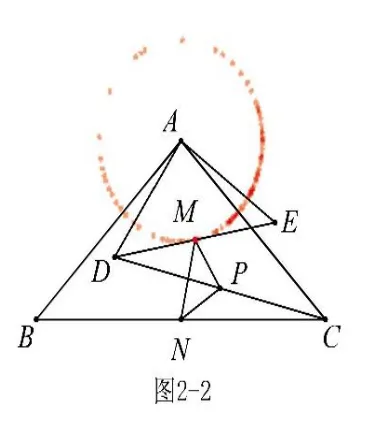
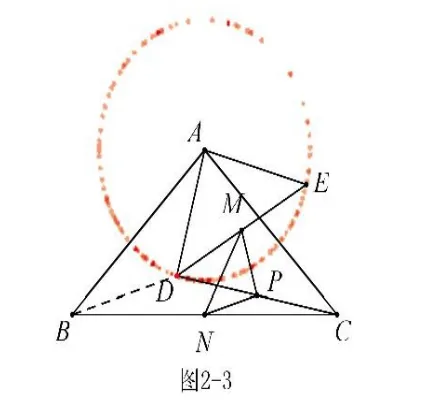
①对于边长MN，N是定点，M是动点.点M是DE 的中点，AM=，在△ADE 绕点A 旋转过程中，点M 也绕点A 旋转（点M 在以A为圆心，为半径的圆上运动，如图2-2），显然MN 最大为，?MN 最小为，?故△PMN 的面积最大为，最小为；②对于边长PN，N是定点，P是动点，但点P 的运动轨迹无法判断（圆心不好确定），因此我们必须找到PN 的“亲戚”来帮助（自己解决不了的事，就要善于找人代劳，这就是所谓的“转化”，“不转化，无数学”），由中位线性质可知，于边长BD，B是定点，D是动点（显然点D 在以A为圆心，4为半径的圆上运动，如图2-3），因此最大为BDAD=10-4=6，MN 最小为AB-AD=10-4=6，同理可求△PMN 的面积最大为，最小为；③对于边长PM，可转化为CE 来解决，不再赘述。

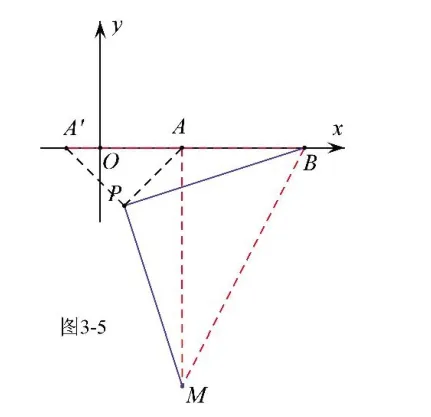
例3 如图3-1，在平面直角坐标系内，点A（2，0），B （5，0），动点P 与A 的距离为2，以P为直角顶点，BP为直角边作等腰直角三角形BPM，求线段AM 的最大值及此时点P 的坐标。

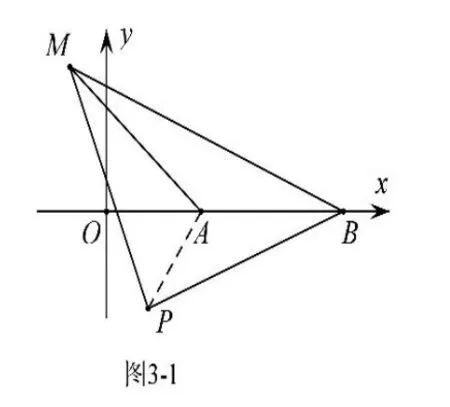
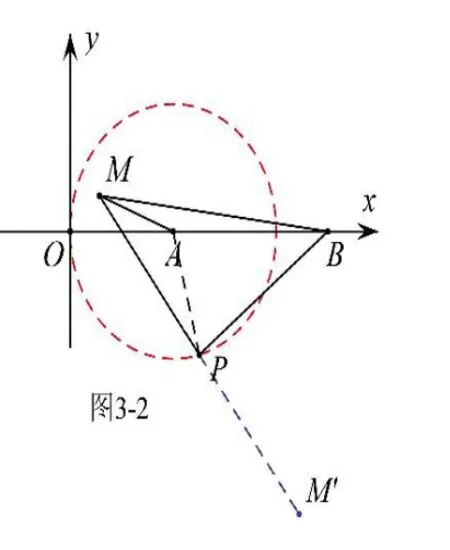
解析：由题意可知，①点P 在以A为圆心，2为半径的圆上运动；②△PBM为等腰直角三角形,其边长随着点P 的运动而变化；③点M 也随着点P 的运动而运动,虽然知道其运动轨迹为圆，但却无法确定其圆心；④由∠BPM=90°，所以点M可能在P 的上方也可能在P 点下方，如图3-2，求解时需分类讨论。

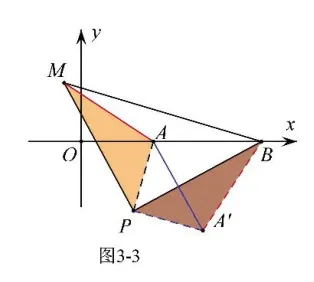
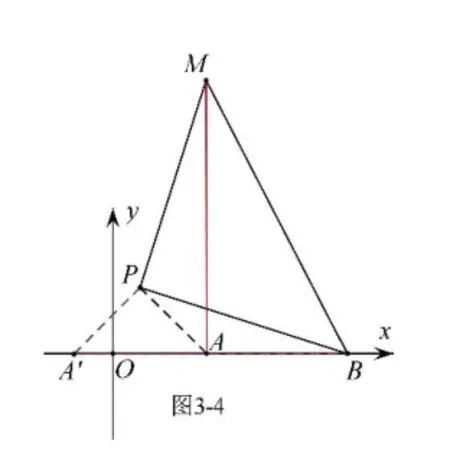
我们以PA为直角边作等腰直角三角形APA’，如图3-3,就将AM 转化为A’ B 了（即AM=A’ B,求线段AM 的最大值就是求A’ B 的最大值），在△AA’ B 中，AB=3，所以A’ B 的最大值为，此时A’ 恰好在射线BA 上，P 在线段AA’的垂直平分线上.当M 在x 轴上方时，点P 坐标为（，）如图3-4；当M 在x 轴下方时，点P 坐标为（，-）如图3-5.