基于复杂网络理论的上证A股网络结构及其特征分析
2020-02-14刘广刘艺萍柯凡尘肖文鑫
刘广 刘艺萍 柯凡尘 肖文鑫

摘 要:基于复杂网络理论,使用上证A股2009—2014年的周收益率数据,根据相关系数大小确定阈值并构建其复杂网络结构,进行网络度数中心性、凝聚子群和小世界效应等特征分析,发现能源、交通运输和房地产类股票在沪市中占据重要地位,其波动对整个市场的影响较大;部分股票在不同“团体”中出现,或与同类股票形成“小世界”。研究揭示了A股市场的微观复杂结构,对把握市场主要矛盾运动和转化方向、实施系统性风险管理等具有重要启示。
关键词:复杂网络;度数中心度;凝聚子群;小世界效应
中图分类号:TP391 文献标识码:A
Abstract:Based on complex networks theory,this paper firstly chooses the weekly earnings data of the Shanghai stock markets stocks during 2009 to 2014.Then this paper determines threshold according to their correlation coefficients,and construct their complex networks.At last,the characteristics of the complex networks,such as degree centrality,cohesive subgroup and small-world effect,are comprehensively analyzed.This paper finds that the stocks of energy,transportation and real estate have been occupying an important position in the Shanghai stock market.Their volatilities have a great impact on the whole market.Some stocks appear in different groups,or form a "small world" with the same kind of stocks.The study reveals the micro-level complex structure of A-share market,which provides important enlightenment to grasp the main contradiction movement,transforming direction of the market,and implement systematic risk management.
Keywords:complex network;degree centrality;cohesive subgroup;small-world effect
1 引言(Introduction)
网络是由节点(Node)和连接节点的边(Edge)组成的复杂结构,主要用来描述事物之间的多元联系。复杂网络(Complex Network)是具有高度复杂性的网络,具有自组织、自相似、自吸引、小世界、无标度等部分或全部特征。复杂网络利用统计学、物理学、计算科学、图论等,描述自然界和人类社会中各种复杂系统及其内在联系,揭示其随时空演化的复杂性和多样性。复杂网络理论在交通、经济、金融、生物和军事等领域得到广泛应用[1-5],日益受到學术研究的重视。
证券市场是一个复杂系统,证券之间存在千丝万缕的联系。经典金融理论对证券市场的研究多基于基本面和技术分析,重视证券的个体和静态特征。其后博弈论和心理学研究方法被逐渐引入金融学领域,因投资者行为导致的证券之间的相互影响(比如相互扰动、波动溢出),或证券作为整体表现出的群体特征(比如同涨同跌),或证券市场存在的各种异象,都获得了研究的广泛关注。随着金融物理学等交叉学科的出现和发展,对证券市场传统认知的缺陷日益显现,与风险管理或资产配置之间的矛盾也日渐凸显。已有研究发现,证券之间的关联程度和相互作用对证券市场的影响已超过基本面因素对证券市场的影响。利用复杂网络模型和方法揭示证券市场的微观结构,并对证券相互作用特征进行定性和定量分析,对深刻认识和把握证券市场运行规律,优化资产配置和实施风险管理都有重要现实意义。
2 文献综述(Literature Review)
复杂网络理论涵盖计算机、图论、社会学、物理学等多个领域。现实世界中的计算机网络、人际关系网络等,虚拟世界中的股票网络、经济网络等,都可看作复杂网络。复杂网络已经成为研究经济、金融网络及其动态演化过程的重要工具(Battiston et al.,2012)[6]。
国外学者早在上世纪末就开始尝试用复杂网络理论来研究证券市场。Watts & Strogatz(1998)[7]首先提出小世界网络模型,Barabasi & Albert(1999)[8]提出无标度网络模型,成为复杂网络模型的雏形。Newman(2003)[9]对复杂网络的小世界效应、幂律分布等性质进行了研究。以相关理论研究为基础,Mantegna(1999)[10]、Micciche et al.(2002)[11]、Kim et al.(2002)[12]与Onnela et al.(2002A,2002B)[13,14]等构建美国证券市场的股票复杂网络进行了网络节点的特性分析。此外,Lee et al.(2007)[15]、Galazka(2011)[16]、Namaki
et al.(2011)[17]与Majapa & Gossel(2016)[18]等分别对韩国、波兰、德黑兰与南非等国家的证券市场的股票复杂网络及其拓扑性质进行了分析。
国内理论研究方面,杨建梅(2010)[19]基于发生学和知识论域视角,从研究范式方面对复杂网络理论进行了详细阐述,为准确使用该理论提供了指导。彭俊好(2014)[20]对伪分形无标度网络和谢宾斯基分形网络的可靠性进行模拟,发现无论是在随机点故障还是边故障下,前者都具有更强的鲁棒性,且节点故障对网络影响比边故障影响更大;但后者具有更好的全端可靠性。这为使用复杂网络模型提供了进一步指引。应用研究方面,杨治辉和贾韩梅(2011)[21]使用相关系数确定网络阈值,建立了股票关联网络并分析了其统计特性。张来军等(2014)[22]分别使用沪深300指数成分股的收益率、成交量、市盈率构建复杂网络,发现股票收益率和成交量指标具有较强的关联性,存在小世界效应,市盈率指标的关联性较弱,不存在小世界效应。此外,曾志坚等(2015)[23]、张骥和龙海明(2017)[24]与惠宝锋等(2018)[25]等分别通过构建新能源板块内88只股票的无向无权网络、基于股价波动的非线性相关性的沪深300指数成分股的复杂网络,以及基于相关系数的关于上证A股的900只股票网络模型进行分析,均发现网络明显具有小世界效应。谢凌峰和陈志新(2016)[26]考察了沪港通实行前后A+H股网络结构的动态变化,发现沪港通实行后网络平均度和集聚系数发生了明显变化,各节点之间联动性增强。
总体看来,国内外应用复杂网络理论探讨证券市场的研究成果不少。这不僅极大拓展了复杂网络理论的应用范围,而且有助于从复杂性角度深刻理解证券市场的静态结构和动态演化特征,为资产配置和风险管理提供了理论指引。但既有研究多是针对证券市场整体实施的,尚缺乏对证券个体禀赋特征的重点关注和深入讨论。这会不经意造成对证券共性与个性特征的割裂,一定程度上从一个极端走向另一个极端,出现过犹不及的情况。由于资产配置的核心要义在于证券分析,因此基于复杂网络视角揭示证券个性特征十分必要。这对同时把握上市公司基本面和网络特征是个有益尝试。
3 研究设计(Research Design)
3.1 样本选择与数据采集
为规避股权分置改革、全球金融危机等重大事件对证券市场冲击带来的影响,首先选择2009年之前在沪市上市的公司为总体样本。然后剔除金融类、被特殊处理(ST或ST*)或发生过重大资产重组的公司,最终得到584个样本。样本期为2009年7月1日至2014年7月31日。为避免临时停牌造成数据大量缺失,使用样本股的周收益率数据计算相关系数;当某个周数据缺失时,令该周收益率为0。数据来源于国泰安数据库(CSMAR),数据处理使用MATLAB7.0软件,复杂网络特征分析使用UCINET和Netdraw软件。
3.2 样本股的复杂网络结构图
借鉴Huang(2009)[27,28]、张来军等(2014)[22]的做法,使用相关系数阈值法来构建网络。对任意的两支股票i和j,定义其周收益率之间的相关系数为ρij,于是ρij∈[-1,1]。当相关系数大于或等于指定的阈值θ时,就认为股票i和j之间有边连接,否则就是无连接。假设连接节点的边没有方向,由此构成股票市场的无向网络图。
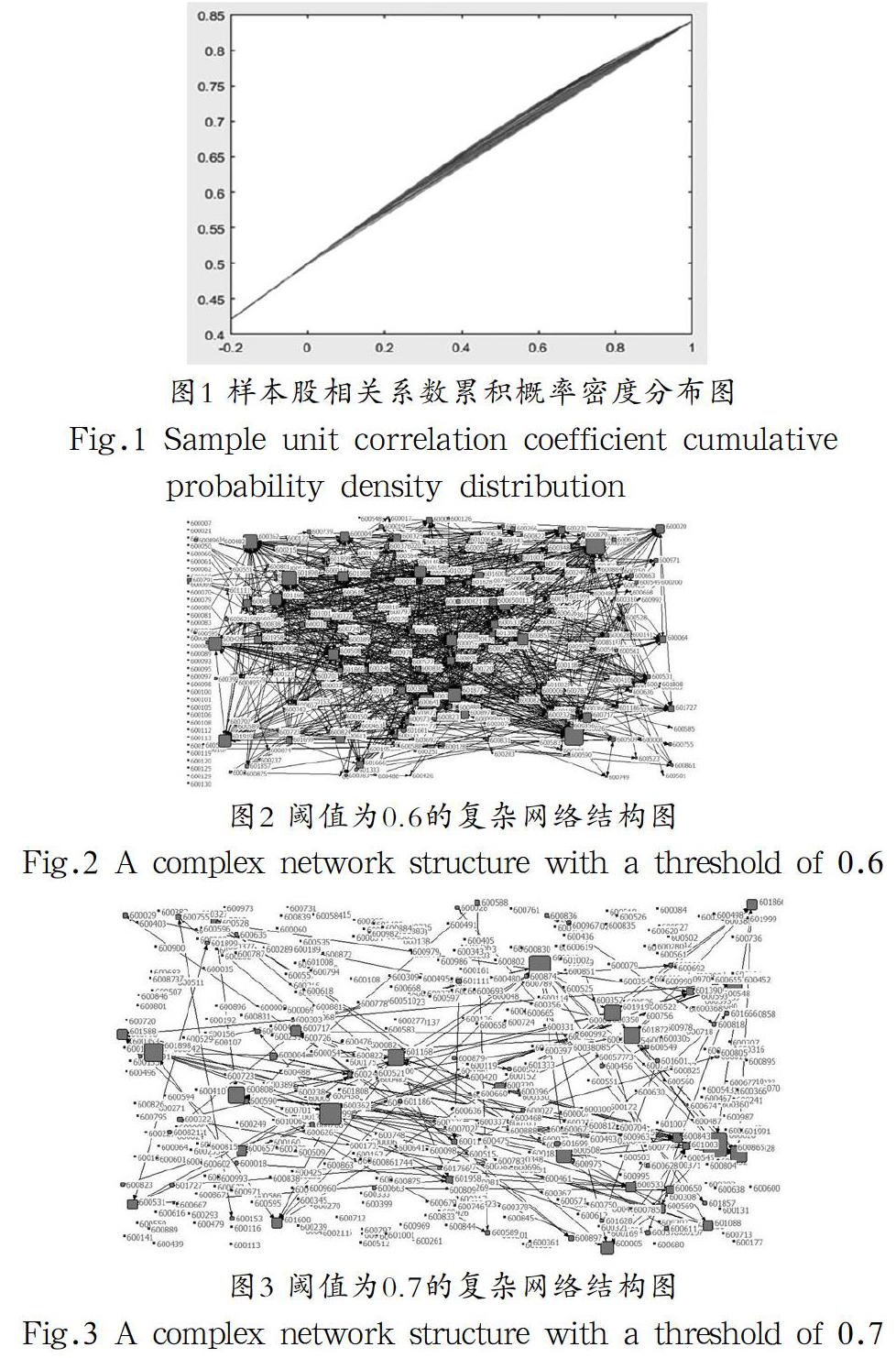
在考察期内,样本股周收益率相关系数的概率分布大部分落在[0.4,0.8]内,并以0.6附近最为集中,如图1所示。参照谢凌峰和陈志新(2016)[26]的做法,选择0.6作为任意两支股票之间是否存在连接的最小阈值,即当两支股票的相关系数大于或等于0.6时,认为其在网络中具有无向边相连,否则认为没有。
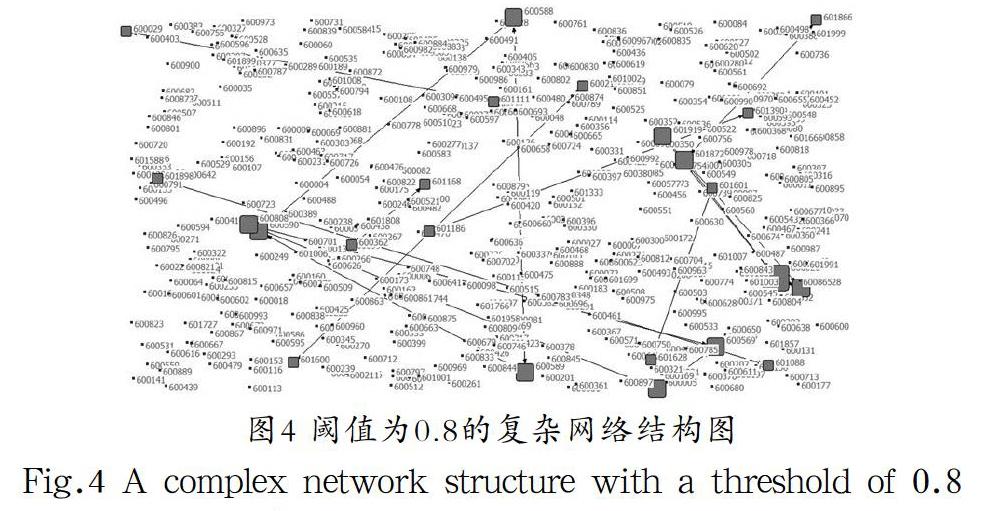
相关系数阈值为0.6、0.7和0.8时,样本股复杂网络结构图分别如图2—图4所示。对比各复杂网络结构图可知,随着相关系数阈值增大,被过滤掉的股票越来越多,网络中的节点越来越少,网络越来越稀疏,包含的有用信息越来越少。由于阈值过大或过小都存在不足,而阈值为0.6时的复杂网络结构图相对比较清晰,节点数量适中,不会遗漏太多有用信息,因此选择该网络结构图作为特征分析对象。
4 网络结构特征分析(Analysis of network structure characteristics)
4.1 度数中心度分析
中心度(Degree)代表节点在网络中的地位或权力,主要有度数中心度、接近中心度和中间中心度三个测度指标。由于我们研究的股票网络属于无标度网络,且存在离散点,因此接近中心度和中间中心度分析不适用,只考察度数中心度。
度数中心度指节点度数与网络规模之比。股票在网络中的度数中心度越大,表明与其他股票的联系越多,与市场的关系越紧密,在网络中的地位越重要。选择阈值为0.6和0.65得到的复杂网络进行对比分析,度数中心度的绝对值和相对值的描述性统计和排名前15的股票见表1和表2。
由表2可知,无论阈值是0.60还是0.65,中远海能(600026)、中煤能源(601898)、南山铝业(600219)和江西铜业(600362)均为度数中心度最高的四只股票,其度数远大于平均度数,在整个网络中占据核心位置。如果继续将阈值提高,发现西部矿业(601168)、北辰实业(601588)、马钢股份(600808)、中远海特(600428)、上海能源(600508)、中国神华(601088)、中远海控(601919)、招商轮船(601872)等几只股票的度数中心度也较高。这表明,在A股市场中,除了金融类股票外,处于重要地位的大多为能源、交通运输与房地产类股票,这与能源、交通运输和房地产行业作为基础行业的特性相一致,也与Nobi et al.(2014)[23]、谢凌峰和陈志新(2016)[26]、张骥和龙海明(2017)[24]等的研究结论相一致。这些行业在产业链中处于核心位置,且对其他行业的溢出效应非常显著。无论是优化资产配置还是实施风险管理,对这些行业都应给予重点关注。
4.2 凝聚子群分析
凝聚子群主要关注复杂网络节点的“成分”和“k-丛”,从互惠角度研究网络的凝聚现象。凝聚子群提供了一个较好的观察股票相似特征的工具和方法。
在阈值为0.6的复杂网络中,可获得六组包含至少三个节点的组系,详见表3。由结果可知,该网络中包含六个成分,其中中煤能源(601898)、南山铝业(600219)、中远海能(600026)等100多只股票为一成分,该成分内股票彼此之间的相关性比较高,而与其他成分内股票之间的关联性比较低。同一成分内股票具有行业或地域相关性,与现实情况也较为一致。
进一步考察建立在度数中心度基础上的小团体。当K=2时,可得到352个至少包含3个节点的小团体。继续提高团体最小节点数量,发现当至少包含12个节点时,可得到18个团体(图5)。由结果可知,武钢股份(600005)、西宁特钢(600117)、南山铝业(600219)、凌钢股份(600231)、江西铜业(600362)、马钢股份(600808)、中国铝业(601600)等金属类股票组成一个小团体。再观察其他小团体,发现包含的也是同一类型企业,与现实情况一致。同时还发现,有些股票同时出现在几个小团体中,说明与其他股票的相关系数较大。这类股票属于系统性重要的股票,其波动对市场整体的影响比较大,需要重点监控。
4.3 小世界效应分析
小世界效应指网络中任意两节点间的平均距离长度随网络节点数量的增加呈对数增长,一般通过计算网络的平均距离长度或聚集系数来判断。证券网络是否具有小世界效应,股票之间能否快捷交换信息,对证券市场整体效率有重要意义。在UCINET中沿着路径Network->Cohesion->Distance进行分析,可得到不同阈值下网络结构的平均距离,详见表4。
选取阈值为0.8的网络结构进行分析,发现距离为1的节点有34个,占总数77.27%;距离为2的节点有6个,占总数的13.64%;距离为3的节点有4个,占总数的9.09%。也就是说,在该股票网络中,任何兩只股票的平均距离是1.318,即任意两只股票只要通过1.318只股票就可以相互建立联系,因此网络是畅通的,信息效率较高。一般认为平均距离值不超过10的网络就可以说具有小世界效应,因此沪市的小世界效应比较明显,市场关联性很高,信息效率较强。
5 结论(Conclusion)
证券市场具有复杂性。利用复杂网络分析方法,基于不同相关系数阈值构建沪市股票的复杂网络结构,并对其特征进行分析,结果发现:能源、交通运输和房地产类企业在网络结构中居于核心地位,其波动对整个市场的影响较大,这与其作为基础周期性行业的特性相吻合;部分股票在不同团体中出现,或与同类股票形成“小世界”,即具有较为显著的行业特征;沪市股票具有较强的关联性,信息效率相对较高,市场有效性程度在提升。
上述研究不仅拓展了复杂网络分析方法的应用范围,为认识证券市场微观结构提供了新的视角,而且对把握证券市场走势和实施风险管理具有重要启示。尽管证券市场中联系是普遍的,但这些联系又不是均衡和等权重的,而是在不同类型股票中表现为不同特征。通过确定最佳阈值构建具有明显拓扑性质的股票复杂网络,有利于对证券市场中的金融现象进行具体分析,为动态把握个股之间、行业之间的相互影响机制机理提供理论依据。投资者在进行资产配置时,不仅应着重挑选来自不同子群或“小世界”中的股票,避免“将鸡蛋放在一个篮子里”所带来的风险,而且可通过监测处于网络核心地位的股票来预测市场整体价格走势。监管层也可按照系统重要性原则,据此对处于网络核心地位的股票和持仓机构进行重点监控,防止系统性风险发生。
参考文献(References)
[1] Wu J J,Gao Z Y,Sun H J.Simulation of traffic congestion with SIR model[J].Modern Physis Letters B,2011,18(30):1537-1542.
[2] Gilchrist S,Zakrajsek E.Credit spreads and business cycle fluctuations[J].American Economic Review,2012,102(4):1692-1720.
[3] 李守伟,何建敏.不同网络结构下银行间传染风险研究[J].管理工程学报,2012,26(4):71-76.
[4] Li S,Jin Z.Dynamic modeling and analysis of sexually transmitted diseases on heterogeneous networks[J].Physica A Statistical Mechanics & Its Applications,2015,427:192-201.
[5] 杨宏伟,张勇,杨学强,等.复杂网络及其在军事领域中的应用研究综述[J].系统科学学报,2013,21(01):84-87.
[6] Battiston S,Gatti DD,Gallegati M,et al.Liaisons Dangereuses:Increasing Connectivity,Risk Sharing,and Systemic Risk[J].Journal of Economic Dynamics & Control,2012,36(8):1121-1141.
[7] Watts DJ,Strogatz SH.Collective Dynamics of‘Small-world' Network[J].Nature,1998(393):440-442.
[8] Barabasi AL,Albert R.Emergence of Scaling in Random Networks[J].Science,1999(286):509-512.
[9] Newman MEJ.The Structure and Function of Complex Networks[J].SIAM Review,2003,45(2):167-256.
[10] Mantegna RN.Hierarchical Structure in Financial Markets[J].European Physical Journal B- Condensed Matter and Complex Systems,1999,11(1):193-197.
[11] Micciche S,Bonanno G,Lillo F,et al.Degree Stability of a Minimum Spanning Tree of Price Return and Volatility[J].Physica A,2002,324(1):66-73.
[12] Kim HJ,Lee Y,Kahng B,et al.Weighted Scale-free Network in Financial Correlations[J].Journal of Physical Society of Japan,2002,71(9):2133-2136.
[13] Onnela JP,Chakraborti A,Kaski K,et al.Dynamic Asset Trees and Black Monday[J].Physica A,2002A,324(1):247-252.
[14] Onnela JP,Chakraborti A,Kaski K,et al.Dynamic Asset Trees and Portfolio Analysis[J].The European Physical Journal B,2002B,30(3):285-288.
[15] Lee KE,Lee JW,Hong BH.Complex Networks in a Stock Market[J].Computer Physics Communications,2007,177(1-2):186.
[16] Ga??zka M.Characteristics of the Polish Stock Market Correlations[J].International Review of Financial Analysis,2011,20(1):1-5.
[17] Namaki A,Shirazi AH,Raei R,et al.Network Analysis of a Financial Market based on Genuine Correlation and Threshold Method[J].Physica A,2011,390 (21-22):3835-3841.
[18] Majapa M,Gossel SJ.Topology of the South African Stock Market Network Across the 2008 Financial Crisis[J].Physica A,2016,445(3):35-47.
[19] 楊建梅.复杂网络与社会网络研究范式的比较[J].系统工程理论与实践,2010,30(11):2046-2055.
[20] 彭俊好.两种网络的可靠性模拟及比较分析[J].广州大学学报(自然科学版),2014,13(5):76-81.
[21] 杨治辉,贾韩梅.股票收益率相关性的网络结构分析[C].中国自动化学会控制理论专业委员会.中国自动化学会控制理论专业委员B卷.北京:科学出版社,2011:5732-5736.
[22] 张来军,杨治辉,路飞飞.基于复杂网络理论的股票指标关联性实证分析[J].中国管理科学,2014,22(12):85-92.
[23] 曾志坚,岳凯文,齐力.基于复杂网络的新能源股票间联动性研究[J].财经理论与实践,2015,36(198):44-49.
[24] 张骥,龙海明.基于系统性风险背景的证券市场网络动态演化[J].求索,2017(4):110-116.
[25] 惠宝锋,葛志远,王咏宁.上证A股市场的复杂网络特性研究[J].软件工程,2018,21(06):11-13;7.
[26] 谢凌峰,陈志新.沪港通下A+H股票网络结构演化的实证分析[J].管理现代化,2016(3):1-4.
[27] Huang WQ,Zhuang XT,Yao S.A Network Analysis of the Chinese Stock Market [J].Physica A,2009,388(14):2956-2964.
[28] Nobi A,Maeng SE,Ha GG,Lee JW.Effects of Global Financial Crisis on Network Structure in a Local Stock Market[J].Physica A,2014,407(C):135-143.
作者简介:
刘 广(1980-),男,博士,讲师.研究领域:资本市场与复杂网络.
刘艺萍(1995-),女,硕士生.研究领域:经济统计. 本文通讯作者.
柯凡尘(2000-),男,本科生. 研究领域:复杂网络.
肖文鑫(1999-),男,本科生. 研究领域:复杂网络.
