陈楠 刘龙 马月

摘要：

基于向量式有限元法对空间格构柱受载荷下的屈曲行为进行数值分析，编制屈曲分析的数值计算程序，通过屈曲平衡路径追踪获得失稳临界载荷，探讨不同加载控制方法对计算结果的影响。考虑材料非线性的影响，对5层空间格构柱的载荷屈曲过程进行分析，获得载荷位移全过程曲线，并与格构柱的加载破坏试验进行对比，结果表明：向量式有限元采用位移控制法能够较好地分析空间格构柱的屈曲失稳破坏过程，获取准确的极限稳定承载力。

关键词：

向量式有限元; 位移控制; 空间格构柱; 屈曲; 失稳

中图分类号：  TU395; TB115.1

文献标志码：  B

Buckling failure of spatial lattice columns based on vector form intrinsic finite element method

CHEN Nan， LIU Long， MA Yue

（Offshore Engineering Institute， Shanghai Maritime University， Shanghai 201306， China）

Abstract：

Based on the vector form intrinsic finite element method， the buckling behaviors of spatial lattice columns under loads are analyzed numerically， and the computing program for buckling analysis is developed， and then the buckling equilibrium path is tracked to obtain critical load of instability. The effects of different load control methods on computed results are discussed. On considering the effects of the material nonlinearity， the buckling process of 5layer spatial lattice column is analyzed， and the loaddisplacement curve of the whole buckling process is obtained. The computed results are compared with the experiment data， and it shows that the displacement controlling mode of vector form intrinsic finite element method is more suitable for analyzing the structural buckling of spatial lattice column. The ultimate stability bearing capacity of the column can be obtained accurately.

Key words：

vector form intrinsic finite element; displacement controlling; spatial lattice column; buckling; instability

0 引 言

格构柱结构能充分利用构件性能、节约材料，在工程中应用广泛。格构柱构件众多，结构高耸且柔度较大，因此整体屈曲破坏前易发生局部构件的屈曲失稳，结构稳定性问题一直是研究的难点。[1]理论分析和有限元法等可为分析失稳问题提供有力支撑。田伟等[2]和赵东东等[3]通过弹性屈曲分析和考虑大变形的弹塑性非线性分析，考察格构柱的稳定性能，但计算过程中需要集成刚度矩阵和求解大量非线性方程，对复杂格构式结构的屈曲路径跟踪仍有一定困难[4]。一般有限元屈曲分析需要先进行预应力分析，再不断更新结构初始屈曲形态，该方法计算效率较低且容易遇到求解不收敛的问题。

向量式有限元法是结合向量力学和有限元概念提出的一种力学计算方法，能够有效求解结构的弹塑性、屈曲失稳、碰撞和倒塌等复杂力学行为。[56]因为该方法的研究对象是结构的众多质点，不需要集成刚度矩阵和迭代求解非线性方程，所以在结构稳定性分析中不需要特殊处理即可越过极值点，能够有效跟踪屈曲和后屈曲变形的全过程。[7]利用该优势，在格构式结构的屈曲失稳破坏研究中，李阿龙等[8]分析结构屈曲路径时提出一种先利用非线性力法预测结构位移方向、再通过向量式有限元法进行修正的方法。陈冲[9]运用向量式有限元梁单元理论，分析格构式结构受到外界载荷冲击后从局部失效到整体倒塌的全过程力学特性。姚旦等[10]利用向量式有限元法研究某大跨越格构式输电塔在风载荷作用下的失稳倒塌问题。这些研究对空间格构式结构的向量式有限元屈曲分析多采用简化的杆单元，大部分没有考虑材料非线性的影响，未能充分利用载荷位移曲线考察结构整体和局部屈曲、失稳的实际过程。

本文基于向量式有限元梁单元理论，利用MATLAB編制计算程序，研究空间格构柱的屈曲破坏过程。通过LEE框架算例讨论位移控制和力控制2种加载方式对分析结果的影响。在考虑材料非线性的基础上，分析5层空间格构柱的弹塑性屈曲破坏过程。

1 向量式有限元基本原理

向量式有限元结构分析基于点值描述、途径单元和逆向运动等3个基本过程。首先，将结构的空间形态用有限数量的点描述，生成节点和单元;然后，通过牛顿运动定律控制节点运动，利用单元逆向运动获取纯变形以计算内力，通过坐标转换确定方向;最后，将在一时间段内结构的运动变形划分为多个时间微段的途径单元，每个途径单元都更新局部坐标系，实现结构位置形状的逐步更新。

向量式有限元结构计算流程如下：

（1）确定结构的材料、截面性质、阻尼、计算步长和总时长等参数。

（2）将结构划分为节点和梁单元。

（3）通过中央差分控制方程计算节点的运动。

（4）由逆向运动获得单元的纯变形，并确定内力的大小和方向。

（5）更新控制方程中的外力和内力。

（6）判断是否达到计算终止时间：若否，则重复第（3）～（5）步;若是，則输出分析结果。

力控制分析和位移控制分析是2种基本的分析方法。力控制法以力为自变量，通过控制方程计算位移响应;位移控制法以节点的位移为自变量，通过节点的反力反求其内力。在屈曲分析中，2种方法各有优劣，应合理选择。

1.1 控制方程及其求解

向量式有限元法的研究对象是一系列空间质点，故其控制方程是一组由牛顿运动定律得到的点运动公式，并运用显式的中央差分公式进行求解。单个质点的平动和转动微分方程分别为

式中：m和I分别为质点的质量和质量惯性矩;x和θ分别为质点的线位移和角位移;F和M分别为作用在质点上的力和力矩。

将上述运动控制方程转化为中央差分形式，即

式中：h为时间增量的步长，可设其为常数;下标中的n表示步数。根据胡克定律，受力后的无阻尼结构将维持持续振动状态，因此在方程中加入虚拟的计算阻尼力，上述差分公式变为

1.2 梁单元内力计算

向量式有限元结构分析中的梁单元分为平面梁单元和空间梁单元2种。平面梁单元的节点位移有3个分量，包括2个平移量和1个转动量，单元内力除轴向力外还有1组剪力和弯矩。空间梁单元节点分量包括3个平移量和3个转动量，经过简化后，单元内力包括轴力、扭矩，以及剪力和弯矩各2组。另外，平面梁单元局部坐标系中的1个主轴方向（垂直于运动平面）不发生变化，而空间梁单元局部坐标系中3个主轴方向均会发生改变。

单元内力大小与纯变形有关。向量式有限元法利用逆向运动概念计算纯变形，建立局部坐标系并根据虚功原理计算内力大小和方向，再通过正向运动（坐标转换）让内力方向回到原来的位置，单元逆向运动示意见图1。若杆单元1a2a经运动变形到达12，则令12进行虚拟的逆向运动，包括平移（-u1）和转动（-θ），可得到杆件的纯变形，即长度变化Δ。

对于梁单元，其纯变形除线位移外还包括角位移。梁单元由ta运动至t的变形示意见图2，其中u1为节点1的位移。节点1和2的转角θ1、θ2分别为β1a与β1和β2a与β2的差量，单元12对1a2a的转角θ为刚体转角。在节点转角θ1和θ2中，一部分为单元的刚体转角，另一部分为单元自身几何变形产生的弯角，由此可得到梁单元2个节点的弯角，即纯变形1和2为

1.3 材料非线性

在结构的破坏过程中，一般同时伴随着几何和材料的非线性问题，只有同时考虑几何大变形和材料弹塑性，才能比较真实地反应结构屈曲破坏过程。

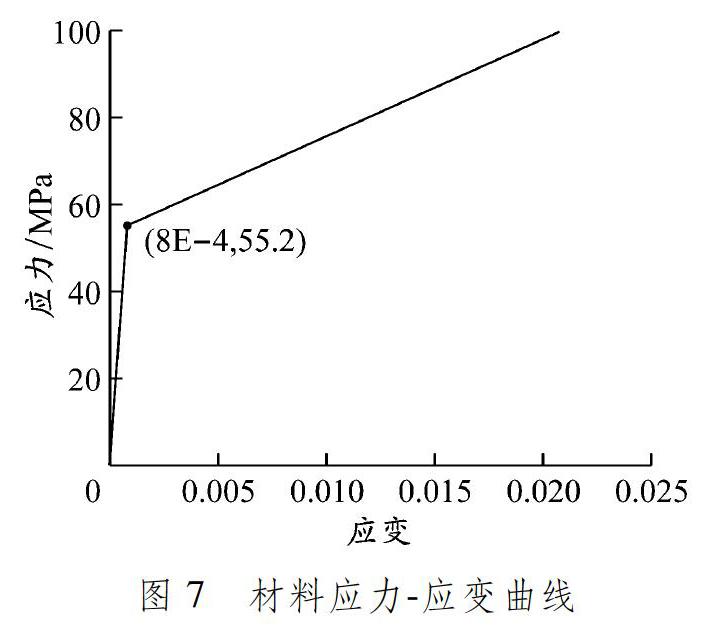
为分析方便，采用双线性强化弹塑性材料模型，见图3。在应力达到屈服应力σy之前材料为完全弹性，应力应变曲线的斜率为弹性模量E;应力达到屈服应力后材料进入塑性阶段，应力应变曲线斜率为切线模量Et，一般可取Et=0.03E。

2 LEE框架算例

LEE框架示意见图4，其受力变形过程具有显著的非线性特征。

框架边长L=120 mm，截面积A=6 mm2，截面惯性矩I=2 mm4，弹性模量E=7.2 MPa。在构件水平段距左端0.2L处加载竖直方向的力F。

用向量式有限元将框架划分20个单元进行分析，分别运用力控制和位移控制加载形式跟踪结构的平衡路径。

分别利用ANSYS和向量式有限元法的位移控制和力控制分析，得到加载点的载荷位移曲线，见图5。本算例属于跃越失稳类型，随着作用力的增大，结构的受力和位移先稳定上升，此时3条载荷位移曲线吻合较好;在位移约49.8 mm时达到临界状态（曲线极值点），之后框架发生跃越翻转，ANSYS分析和位移控制曲线均开始下降，此时结构呈现负刚度状态，尽管两者此时没有吻合，但该下降段代表结构处于不稳定的平衡状态，载荷位移曲线并不具有实际意义;当力控制曲线越过失稳载荷值后，微小的力增量会引起结构位移的徒增，该段并非结构的平衡路径;在结构失稳翻转后，其变形缓慢增大，3条曲线再次吻合。

由ANSYS分析得到的失稳载荷为18.8 kN，向量式有限元法位移控制分析得到载荷为19.1 kN，二者误差仅为1.6%。向量式有限元法位移控制屈曲分析能够有效越过极值点，并追踪结构屈曲和后屈曲过程的平衡路径，而力控制分析相对没有此优势。因此，应用向量式有限元法进行屈曲分析应尽量采用位移控制方式。

3 空间格构柱的屈曲过程分析

5层空间格构柱的有限元模型[11]见图6，该格构柱由主肢杆、水平杆和斜缀条组成。杆件长度均为120 mm，截面均为8.0 mm×1.9 mm，材料为6061铝合金，弹性模量为68.9 GPa，受压屈服强度为55.2 MPa，泊松比为0.33。

格构柱底端固定，在顶端竖直向下施加载荷并限制顶端节点的水平位移，运用向量式有限元法空间梁单元进行仿真分析。为提高计算效率，将每个杆件划分为3个单元，模型共有192个单元和152个节点。采用位移控制加载方式，加载速度为2.5×10-3 mm/s。

格构柱受载屈曲过程具有显著的几何非线性和材料非线性特点。向量式有限元法分析时，以前一个途径单元为参考不断更新主轴坐标，实现结构形状和位移的逐步更新，故其具有二阶分析的特点。在考虑结构的材料非线性时，弹塑性材料的应力应变曲线见图7。

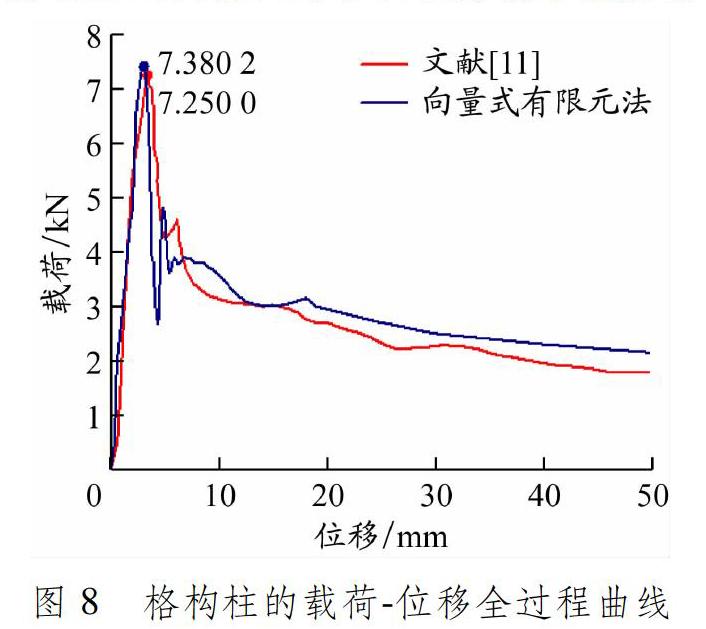
向量式有限元法分析和文献[11]格构柱竖直加载方向的载荷位移全过程曲线见图8。2条曲线总体上趋势一致;在位移0～3.5 mm段2条曲线吻合较好，在位移约3.5 mm处曲线的极值点，即结构的极限载荷处，二者误差仅为1.8%;越过此极值点后，当位移达5.0 mm时发生二次失稳;在结构的主要承载杆件屈曲破坏后，格构柱的稳定承载能力逐渐减弱直至丧失。

向量式有限元法分析得到的3个不同加载位移时格构柱的变形见图9。加载位移为1.0 mm时，结构只是处于轴向压缩状态，没有发生侧向变形;加载位移为5.0 mm时，格构柱第三层肢杆率先发生屈曲失稳;加载位移达到45.0 mm时，格构柱的多个杆件相继屈曲失效，其中第三层杆件屈曲变形最为显著。文献[11]中格构柱的屈曲变形主要发生在第三、四层肢杆，破坏后的格构柱屈曲形态也与向量式有限元法的分析结果相似。

向量式有限元法屈曲分析得到的格构柱主要失稳部位与试验结果相符，失稳载荷与试验值接近，验证向量式有限元法屈曲分析的有效性。

向量式有限元法的分析结果与试验结果出现差异：一方面可能

是因为格构柱试件存在初始缺陷，如初始弯曲、初始偏心等，所以在试件加载过程中，力的方向很难做到一直保持垂直状态，可能会偏移;另一方面，向量式有限元利用中心差分方程进行迭代，受时间步长的影响，计算结果的精度也有待进一步提高。

4 结 论

基于向量式有限元梁单元理论，利用MATLAB软件编制程序进行格构式结构的屈曲行为分析，不需要特殊处理即可有效分析格构柱大变形、大变位、弹塑性等复杂力学问题，主要得出以下结论：

（1）考虑几何非线性和材料非线性特点，向量式有限元能够有效求解得到空间格构式结构的屈曲平衡路径和失稳载荷，从而为工程上钢结构稳定性设计分析提供参考。

（2）对于载荷位移曲线具有极值点的跃越失稳和极值点失稳问题，采用位移控制分析更有优势，能够获取曲线下降段和精确的失稳载荷。

（3）向量式有限元直接对所有节点和单元进行数值计算，能够判断超静定结构局部失稳和整体失稳的关系，并能获取有效的结构后屈曲行为。

基于本文分析结果，应进一步提高向量式有限元法的计算精度和效率;同时结合可靠的试验数据，引入向量式有限元板单元、固体单元等，进行精细化结构失稳断裂分析。

参考文献：

[1]何静. 起重机桁架臂非线性稳定性有限元分析[D]. 大连： 大连理工大学， 2017.

[2] 田伟， 赵阳， 向新岸， 等. 考虑弯矩作用梭形钢格构柱的稳定性能[J]. 土木建筑與环境工程， 2010， 32（6）： 2227. DOI： 10.3969/j.issn.16744764.2010.06.004.

[3] 赵东东， 张益国， 李占岭， 等. 悬索拉线塔主柱整体稳定极限承载力研究[J]. 电力科学与工程， 2015， 31（12）： 4751. DOI： 10.3969/j.issn.16720792.2015.12.009.

[4] KONG X C， QI Z H， WANG G. Elastic instability analysis for slender latticeboom structures of crawler cranes[J]. Journal of Constructional Steel Research， 2015， 115： 206222. DOI： 10.1016/j.jcsr.2015.07.027.

[5] 丁承先， 段元锋， 吴东岳. 向量式结构力学[M]. 北京： 科学出版社， 2012.

[6] WU T Y. Dynamic nonlinear analysis of shell structures using a vector form intrinsic finite element[J]. Engineering Structures， 2013， 56： 20282040. DOI： 10.1016/j.engstruct.2013.08.009.

[7] 王震， 赵阳， 杨学林. 平面薄膜结构屈曲行为的向量式有限元分析[J]. 浙江大学学报（工学版）， 2015， 49（6）： 11161122. DOI： 10.3785/j.issn.1008973X.2015.06.016.

[8] 李阿龙， 袁行飞， 梁笑天. 基于非线性力法及向量式有限元法的结构屈曲路径跟踪[J]. 空间结构， 2017， 23（3）： 8996. DOI： 10.13849/j.issn.10066578.2017.03.089.

[9] 陈冲. 基于向量式有限元的索杆结构精细化分析和倒塌破坏研究[D]. 杭州： 浙江大学， 2017.

[10] 姚旦， 沈国辉， 潘峰， 等. 基于向量式有限元的输电塔风致动力响应研究[J]. 工程力学， 2015， 32（11）： 6370. DOI： 10.6052/j.issn.10004750.2013.08.0795.

[11] 赵徐， 董达善， 滕媛媛， 等. 格构柱非线性全过程分析与试验[J]. 计算机辅助工程， 2018， 27（4）： 5659. DOI： 10.13340/j.cae.2018.04.012.

（编辑 武晓英）