Feng Huang (黄凤) and Han-Shuang Chen (陈含爽)

1School of Mathematics and Physics,Anhui Jianzhu University,Hefei 230601,China

2School of Physics and Materials Science,Anhui University,Hefei 230601,China

Abstract Heterogeneous mean-field theory is commonly used methodology to study dynamical processes on complex networks,such as epidemic spreading and phase transitions in spin models.In this paper,we propose an improved heterogeneous mean-field theory for studying the Ising model on complex networks.Our method shows a more accurate prediction in the critical temperature of the Ising model than the previous heterogeneous mean-field theory.The theoretical results are validated by extensive Monte Carlo simulations in various types of networks.

Key words: heterogeneous mean field theory,Ising model,phase transition

1 Introduction

Many social,biological,and physical phenomena can be well understood on the top of complex networks.[1−6]A common topic in the research community is to establish the relationship between the topologies and the dynamics on them.Owing to degree heterogeneity in the interacting patterns,many fascinating phenomena have been revealed,such as the anomalous scaling behavior of Ising model,[7−11]a vanishing percolation threshold,[12−13]the absence of epidemic thresholds that separate healthy and endemic phases[14−16]and explosive emergence of phase transitions.[17−30]

The heterogeneous mean-field (HMF) theory has been widely used to study dynamical processes on complex networks.[3,5−6]This theory is based on the assumption that the nodes of the same degree are statistically equivalent.The main purpose of the HMF theory is to derive the dynamical equations for the quantities of interest in different degree classes.In general,the set of dynamical equations are intertwined with each other.However,for degree uncorrelated networks,they can be reduced to a single equation for an order parameter,such as the average magnetization in the Ising model[8]and the average infection probability in the susceptible-infected-susceptible model.[14]By linear stability analysis near the phase transition point,the HMF theory can produce an elegant analytical result of the phase transition point.For example,it has been shown that the critical temperature of the Ising model isis thenth moment of degree distributionP(k).For scale-free networks,P(k)∼k−γwith the exponentγ <3,is divergent,and thusTc→∞.The HMF theory has also shown its power in many other models,such as rumor spreading model,[31−32]metapopulation model,[33]zero-temperature Ising model,[34−35]majority-vote model,[36−37]etc.

In the present work,we propose an improved heterogenous mean-field (IHMF) theory to study the Ising model on complex networks.We derive the mean-field equation and then obtain the critical condition under which the phase transition temperature should be satisfied.Under the approximation of large average degree,the phase transition temperatureTcis given analytically,that is different from the result of the HMF theory,By extensive Monte Carlo simulations in diverse types of networks,we find that our theoretical result is more successful in predictingTcthan the previous HMF theory.

2 Model and Simulation Details

The Ising model in a network of sizeNis described by the Hamiltonian,

where spin variableσiat nodeitakes either+1(up)or−1(down).J >0 is the ferrimagnetic interaction constant.The elements of the adjacency matrix of the network takeAij=1 if nodesiandjare connected andAij=0 otherwise.

The Monte Carlo(MC)simulation is performed by the so-called Glauber spin-flip dynamics,[38]in which one attempts to flip each spin once,on average,during each MC cycle.In each attempt,a randomly chosen spiniis tried to flip with the probability

whereβ= 1/(kBT) is the inverse temperature,kBis the Boltzmann constant,andis the energy change due to the flipping process.

3 Theoretical Results

Let us definemkas the average magnetization of a node of degreek,i.e.,whereNkis the number of nodes of degreek.For a network without degree correlation,the probability of an end node of a randomly chosen edge having connectivitykis,[3]whereP(k)=Nk/Nis the probability of a randomly chosen node having connectivityk,andis the average degree.Thus,the average magnetization of an end node of a randomly chosen edge can be written as,

This implies that the spin orientation of an end node of a randomly chosen edge points up or down with the probability (1+)/2 or (1−)/2,respectively.Thus,for a node of degreek,the probability that there arenup spins among the neighborhood of the node can be written as a binomial distribution

whereCnk=k!/[n!(k −n)!]is the binomial coefficient.For an up-spin node of degreekwithnup-spin neighbor,the energy change to flip this spin is 4n −2k.Combining Eqs.(2) and (4),we can write down the probability of flipping an up-spin node of degreek,

Likewise,we can express the probability of flipping a down-spin node of degreekas

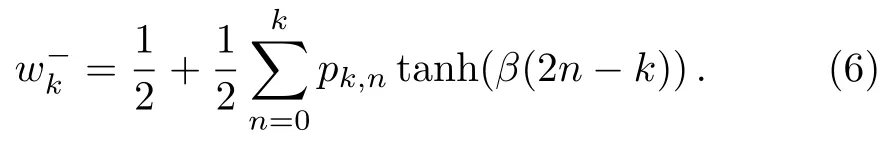
At each spin-flip process,the expectation of the change inmkcan be written as

where the factor isNk/Nwhich is the probability that a class of nodes of degreekare chosen,and2/Nkis the change inmkdue to the flip of an up (down) spin of degreek,and (1±mk)/2 is the probability of an up (down)spin of degreekis chosen.If we set ∆t= 1/N,Eq.(7)can be rewritten as

Substituting Eq.(3) into Eq.(8),we arrive at a selfconsistent equation of ˜m,

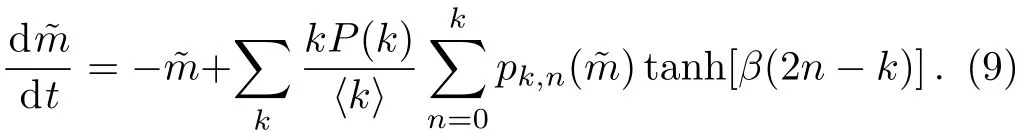
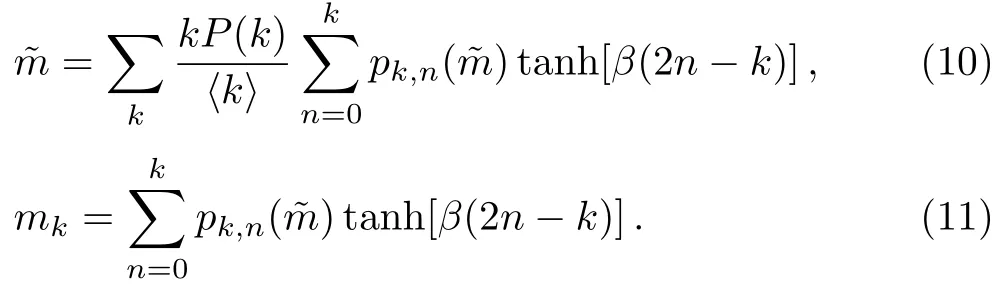
Considering the fact

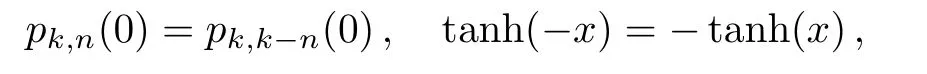
it is not hard to verify that= 0 is always a solution of Eq.(10).Such a trivial solution corresponds to a disordered phase.The other solutions corresponding to0 (an ordered phase) exist when the solution of= 0 loses its stability.This requires that the derivative of the right hand side of Eq.(10) with respect tois larger than one at= 0.The requirement yields the critical temperature of the Ising model that separates the disorder phase and ordered phase.To the end,we expandpk,naround= 0 to the first order,pk,n() =pk,n(0)+pk,n(0)(2n −k)+O() withpk,n(0) =Cnk(1/2)k.The critical temperature is determined by

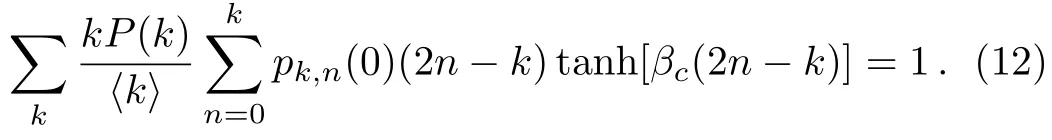
Equation (12) is the main result of the present work.For a given degree distributionP(k),the critical temperatureTc= 1/βccan be calculated numerically by Eq.(12).Moreover,for networks with large average degree,βcapproaches to zero.To the end,we expanse

and substitute Eq.(13) into Eq.(12),we have

where

Substituting Eqs.(15) and (16) into Eq.(14),we obtain

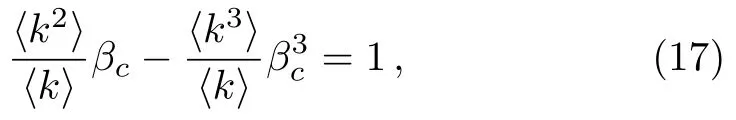
If we drop out the second term on the left hand side of Eq.(17),we recover to the result of the HMF theory,

Substituting Eq.(18) into Eq.(17),we arrive at an improved result of the HMF theory,

4 Numerical Validation

In order to validate the theoretical result,we need to numerically determineTc,which can be located by calculating the so-called Binder’s fourth-order cumulantU,[39]defined as whereis the average magnetization per node,denotes time averages taken at equilibrium,and[·] stands for the averages over different network configurations for a given degree distribution.Tcis estimated as the point where the curvesU ∼Tfor different network sizesNintercept each other.

We first show the results in regular random networks(RRNs),in which each node is randomly connected to exactlykneighbors and degree distribution follows theδ-function,and thus

In Fig.1(a),we showUas a function ofTfor different network sizesNin RRNs withk= 4.The intersection point locates the critical temperatureTc=2.88,which is closer to our theoretical resultk−1=3(Eq.(22))than the previous onek= 4 (Eq.(21)).In Fig.1(b),we compare the numerical results ofTcwith the theoretical predictions for differentk’s in RRNs.It is obvious that our improved theory is superior to the previous HMF theory.

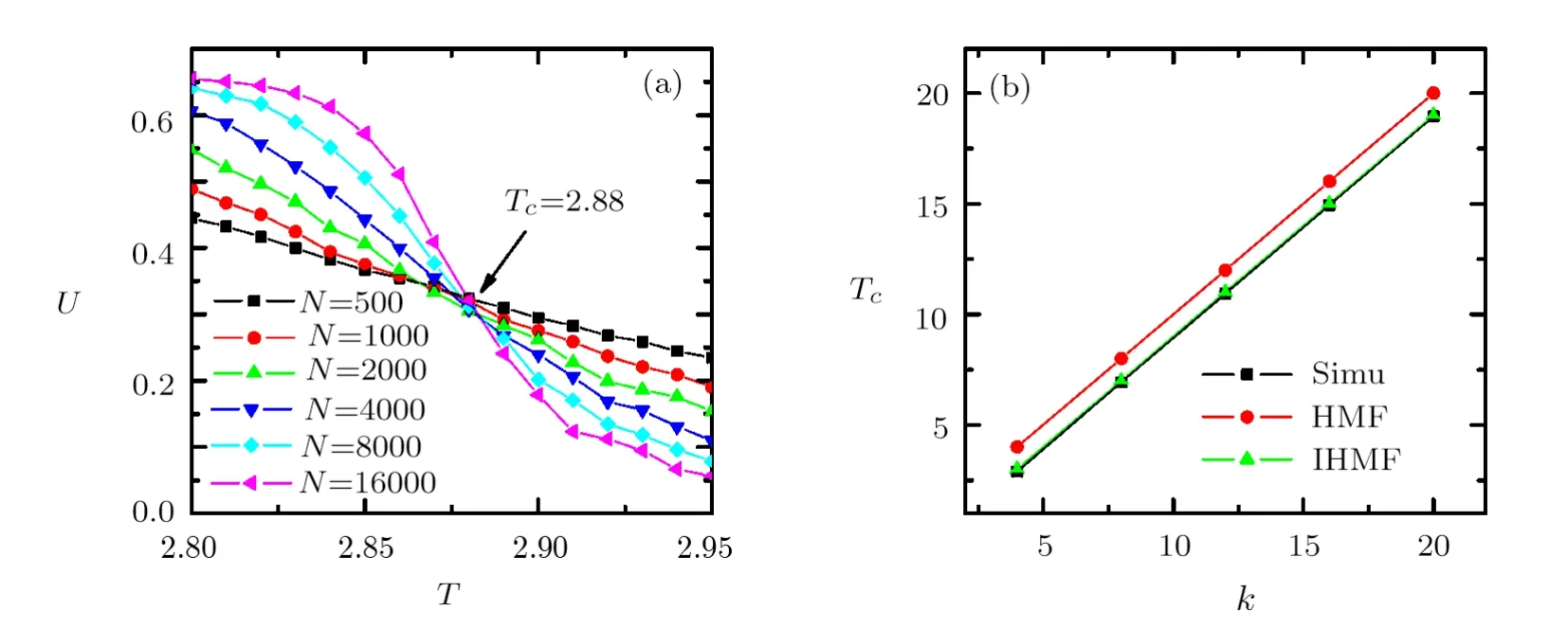
Fig.1 (Color online) (a) The Binder’s fourth-order cumulantU as a function of the temperatureT for different network sizesN in RRNs withk =4.(b) The critical temperatureTc in RRNs as a function ofk.

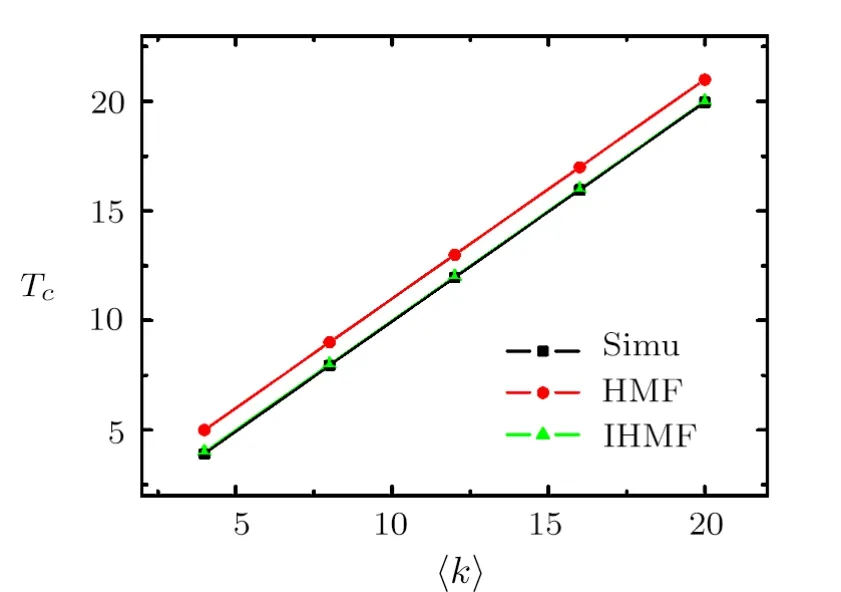
Fig.2 (Color online)The critical temperatureTc in ER random networks as a function of average degree〈k〉.

In Fig.2,we compare the numerical results ofTcwith the theoretical predictions for different average degree〈k〉in ER random networks.As expected,our improved theory is superior to the previous HMF theory.

For scale-free networks (SFNs) whose degree distribution follows a power-law function,

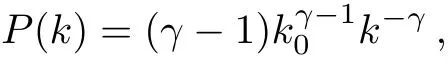
with the minimal degreek0and the power exponent of degree distributionγ,we have

As mentioned before,for SFNs withγ ≤3,is divergent in the limit ofN →∞,and thusTc→∞.While for 3< γ ≤4,is divergent in the limit ofN →∞,and therefore Eq.(26)is only valid forγ >4.In Fig.3(a)and 3(b),we show the results in SFNs withγ= 4.5 andγ=5.0,respectively.It is obvious that our improved theory is more in agreement with the simulation results than the previous HMF theory.

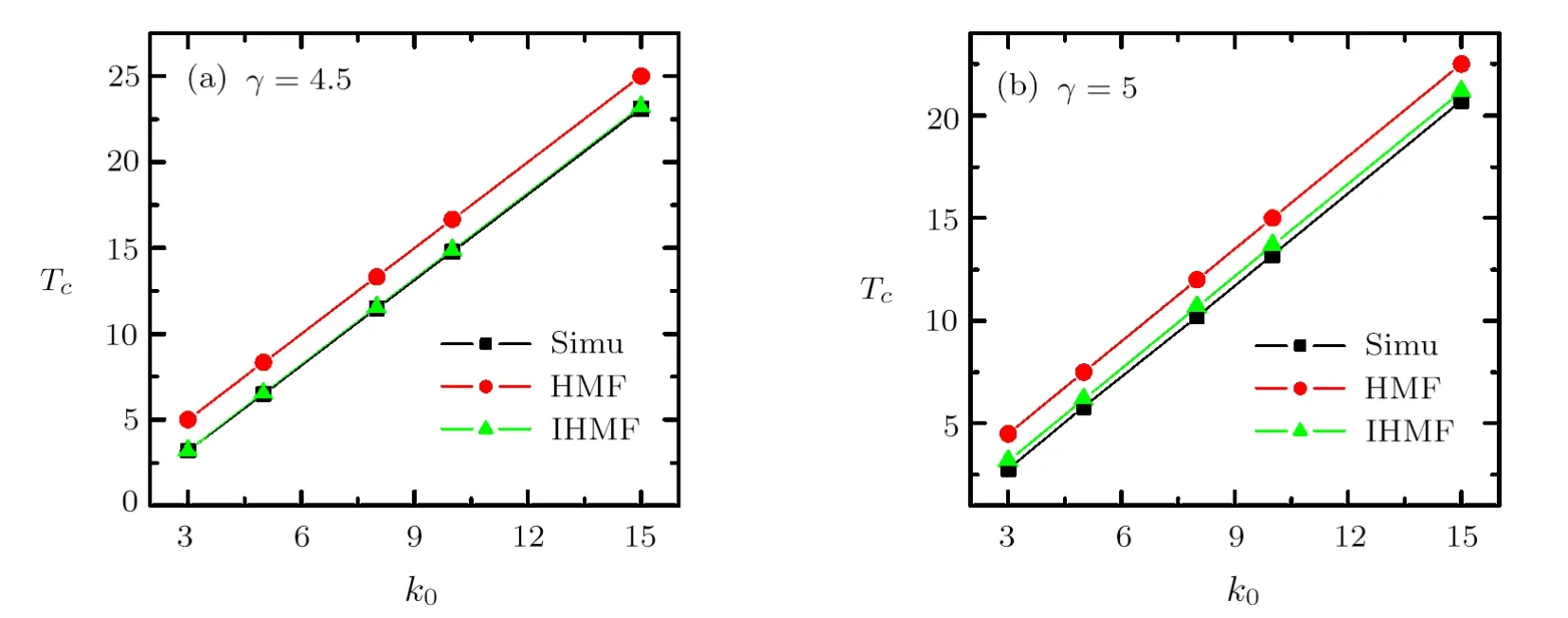
Fig.3 (Color online)The critical temperatureTc in SF networks as a function of minimal degreek0.(a)γ =4.5;(b)γ =5.

Fig.4 (Color online) The critical temperatureTc in random networks with a bimodal degree distributionP(k) = (1/2)δ(k −−∆)+(1/2)δ(k −+∆) with=10.

At last,we construct a network with degree distribution following a bimodal distributionP(k) =We haveIn terms of Eqs.(18) and (19),we can obtain the results of the HMF and IHMF theories.As shown in Fig.4,the IHMF theory is more accurate in predicting the critical temperature than the HMF theory.

5 Conclusions

In conclusion,we have proposed an improved heterogeneous mean-field theory to study the Ising model on complex networks.Our theory shows that the critical temperature of the Ising model isthat is an improvement of the result of the customary heterogeneous mean-field theory,.By comparing the critical temperature with simulations in various networks,we have shown that our theoretical prediction is more accurate than the previous heterogeneous mean-field one.