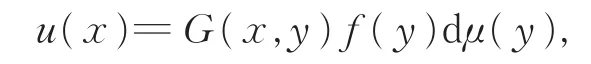SG3左半定义域上的Dirichlet边值问题
2019-12-19蔡洁洁吴波
蔡洁洁,吴波
(南京财经大学应用数学学院,江苏南京210023)
0 引言
自1828年,英国人GREEN引入了一个以其姓命名的重要函数后,格林函数在数学物理方法中一直扮演着十分重要的角色。
格林函数在数学物理领域是一个十分重要的概念,经常出现在常微分方程、椭圆型和抛物型偏微分方程的边值问题中。利用格林函数可以将微分方程的边值问题转化为积分方程。求解Laplace方程、Helmholtz方程等,关键在于确定相应的格林函数,而确定格林函数的难度取决于边界形状。
ROBERT[1]和JUN[2-3]研究了[0,1]区间上的Dirichlet边值问题,试图求出该边值问题的解,利用文献[4]中Sierpinski垫片上微分方程的辅助计算给出了格林函数的表达式。ROBERT[1]首先通过“帐篷函数”,将[0,1]区间上的格林函数推广到Sierpinski垫片,并且得到了Sierpinski垫片上格林函数的表达式。
本文的研究主要基于文献[5],一开始通过不同的位置,对Sierpinski垫片进行水平切割,得到不同Sierpinski垫片的上半定义域;在讨论过程中给出了Sierpinski垫片特定定义域上Dirichlet边值问题的解的延拓算法和具体表达式;同时也刻画了在Sierpinski垫片特定定义域上的所有调和函数的特点。紧接着,JOHN等[6]和GUO等[7]将其推广到一般的情形。ROBERT[8]也讨论了Holder-Zygmund、Besovan和Sobolev 3种不同分形类型的函数空间,为解决不同的自相似图形上的Dirichlet边值问题提供了新的思路。JUN[9-10]探讨了在p.c.f自相似集上的调和函数的相关计算。本文所涉及的调和函数的一些性质可参见文献[9-10]。
LI等[11]沿着SG的底边中心点进行垂直切割,得到新的自相似图形;在此基础上研究了SG上的左半部定义域的一些性质,以及在该定义域上的Dirichlet问题;尝试求解Dirichlet问题的解的具体表达式,并探讨在该定义域上的正则导数与能的估计范围。
受QIU等[12-15]的启发,笔者试图对SG3进行适当的切割,研究SG3上的某一部分的定义域,探讨在该定义域上是否有类似于Sierpinski垫片上的性质和定理。
1 预备知识
定义1[14]设m∈N具迭代水平,对于
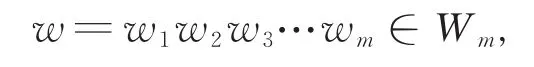
其中,
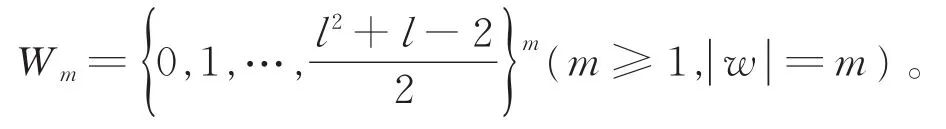
定义2[1]记x~my当且仅当x≠y并且x,y∈Vm同属于一个胞腔。
定义3[1]设m∈N,则SGl的第m次迭代Γm上离散的电阻形式可由下式给出:
εm(u,v)=r-m(u(x)-u(y))(v(x)-v(y)),
其中,u,v是定义在Vm上的函数
图1给出了SG3上的前2次迭代Γ1,Γm。

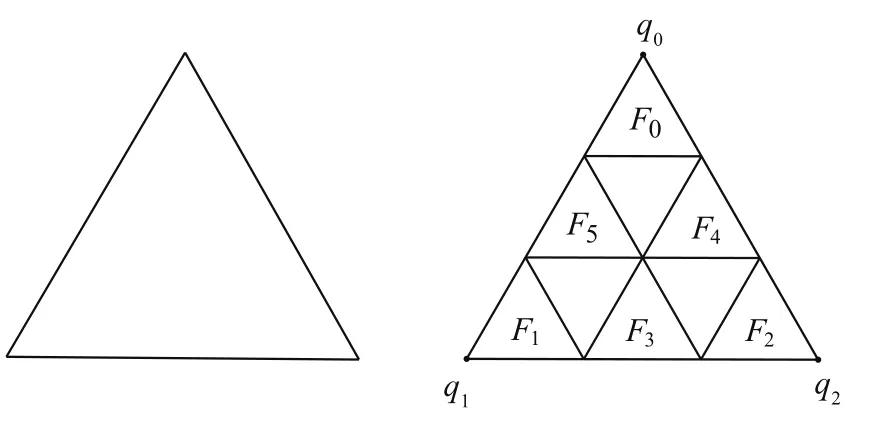
图1 SG3上的Γ1,Γ2Fig.1 Γ1,Γ2ofSG3
定义4[10]定义为函数u的能,并且u属于dom ε当且仅当ε(u)<∞。
定义5[10]定义SGl上的电阻形式为
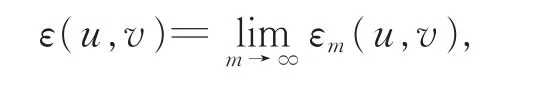
其中u,v∈ dom ε。
定义6[1]函数u在边界点qi∈V0的正则导数可通过下式定义:
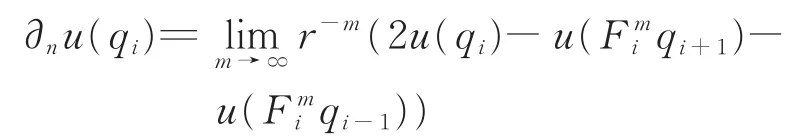
类似地,也可得到其他点的正则导数的表达式。
定理1[10]调和函数h满足平均值性质,也就是说,对于每一个迭代水平m≥1,有
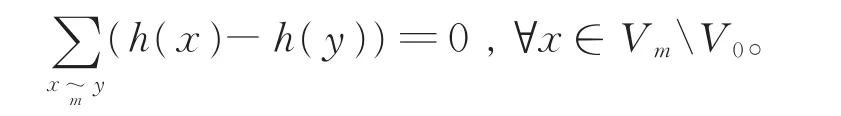
定理2[1](高斯-格林公式)假设u∈dom Δμ,则对所有的qi∈V0,有正则导数∂nu(qi)存在,并且
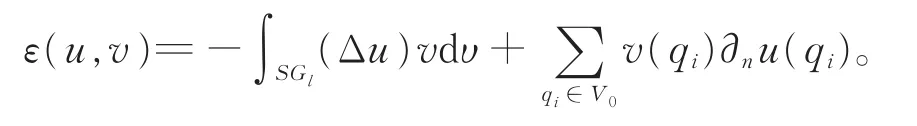
命题1[10]考虑SGl的左半定义域上Ω的Dirichlet问题
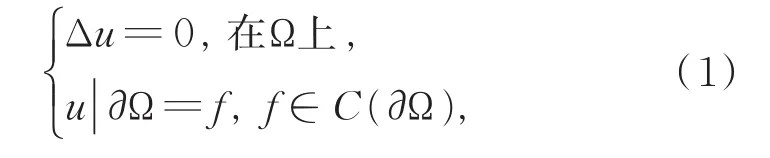
则方程(1)有唯一解。
注 证明过程需用到文献[15]中的引理8.2。
在等边三角形底边的中点处,沿垂直底边进行切割,得到的是SG3的左半部分。第1次迭代后,会产生2个相同的三角形,分别为F1SG3和F5SG3,以及2个半直角三角形F0和F3。在第2次迭代中,将2个大的三角形固定不动,依据SG3原有的迭代规则对2个直角三角形进行2次迭代,依次进行,得到新的图形,如图2所示。所得到的图形具有自相似结构。现在来研究此图形的性质。
定义7[10]SG3上的左半定义域Ω可由水平集上的斜对称调和函数ha来定义,其中ha在V0上的函数值记为,因此
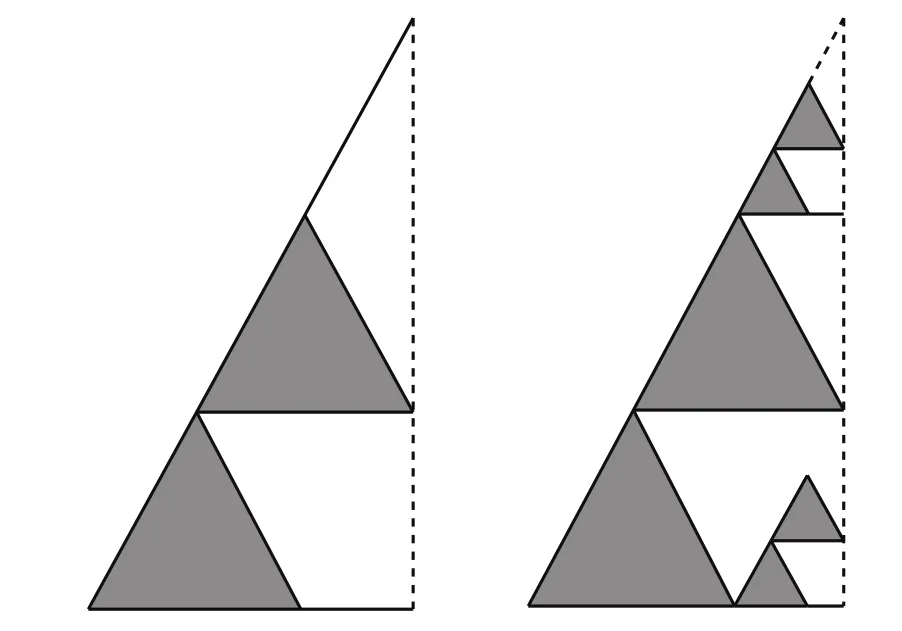
图2 定义域ΩFig.2 Domain ofΩ
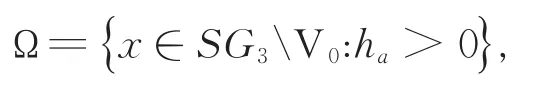
其边界为
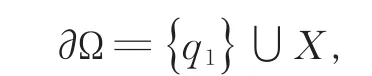
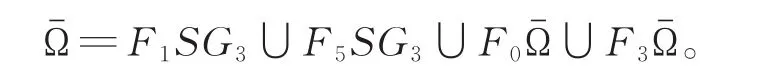
为研究Dirichlet问题解的格林函数,需要对图形中某些点进行标记,见图3。用x∅,y∅和z∅分别表示V1∩的顶点,其中,
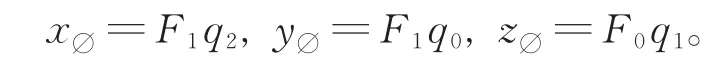
同样,记
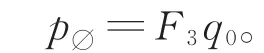
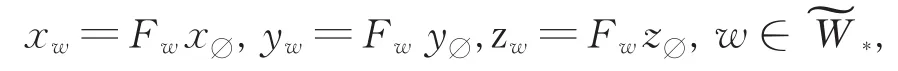
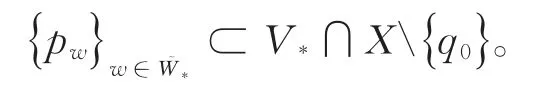
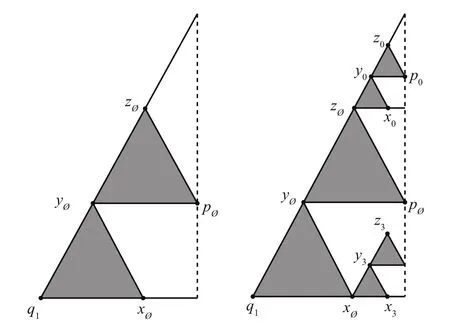
图3 定义域Ω的标记Fig.3 The mark of Ω
2 主要结果
在Ω上,希望得到类似于SG上的格林公式,即形如
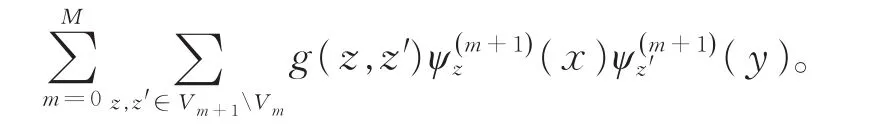
下面分2步进行求解:
第1步当m=0时,在V1∩中有4个点x∅,y∅,z∅和p∅,记
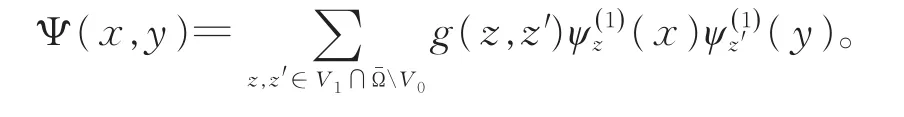
同时,希望得到
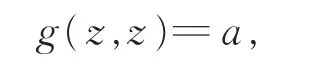
并且,若当z≠z′时,
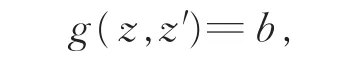
其中a和b是唯一确定的常数。这样,就可以得到所希望的格林函数:
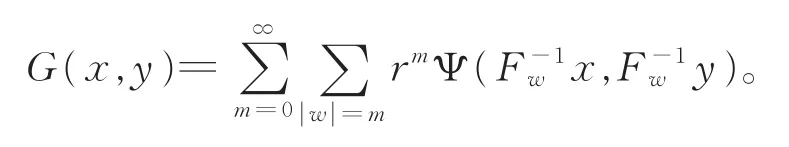
其中,

为计算简便,可采用弱化公式:
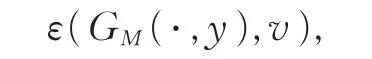
其中,v∈ dom0ε。由此,可计算

得到
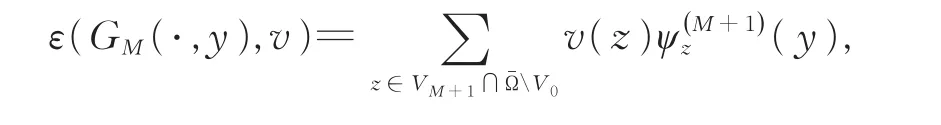
两边同乘以f(y),得到
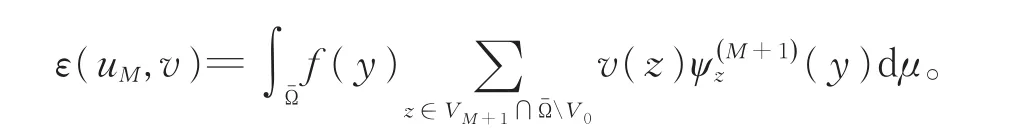
因此
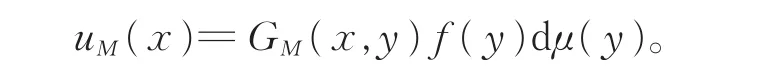
当M→∞时,
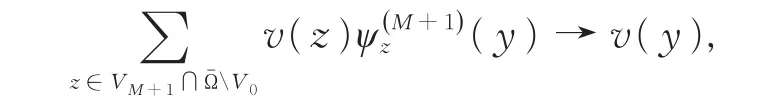
并且是一致收敛的。
由于-Δμu=f,得到
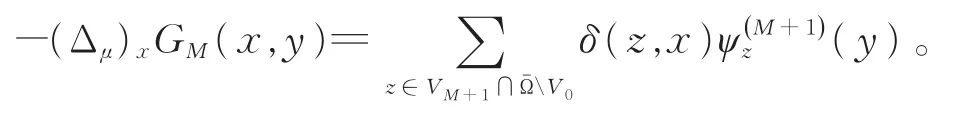
第2步求格林函数中各个参数的表达式。
当M=0时,
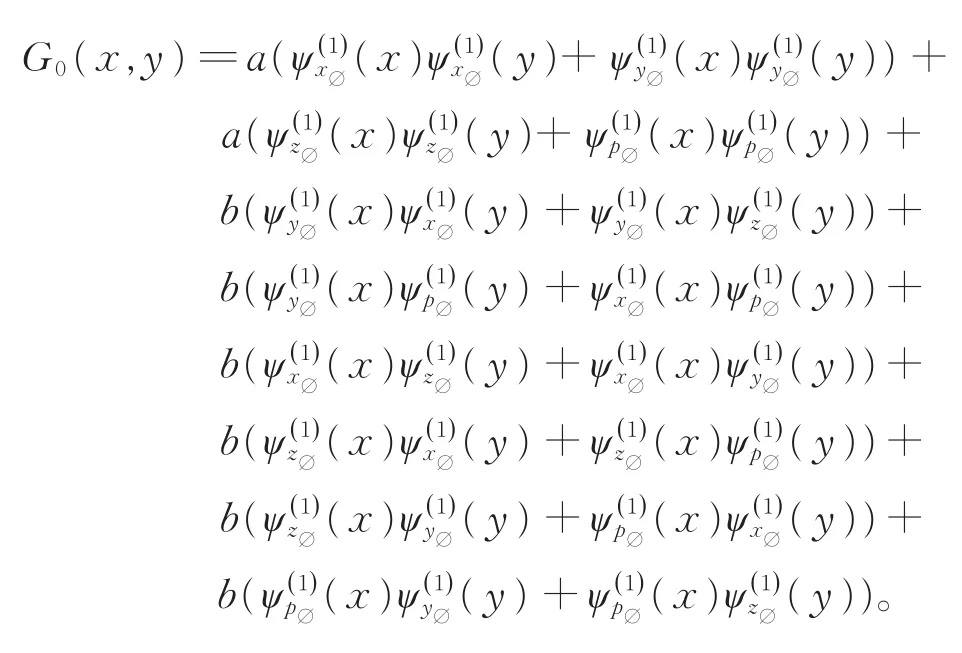
而
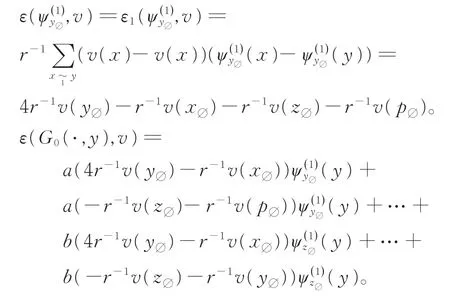
则含v(y∅)的项为
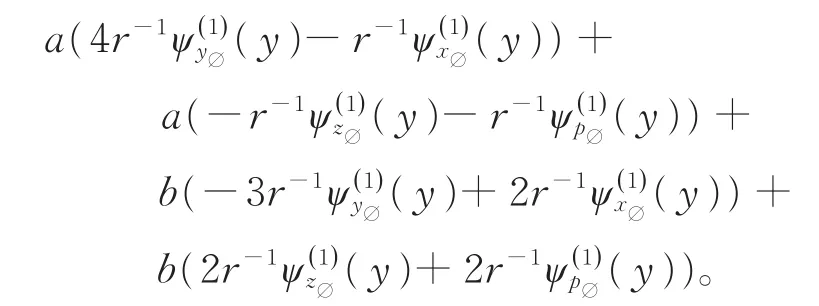
希望得到v(y∅)乘以的形式,只需解线性方程组
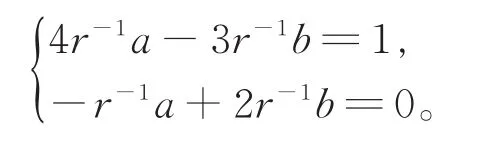
解得
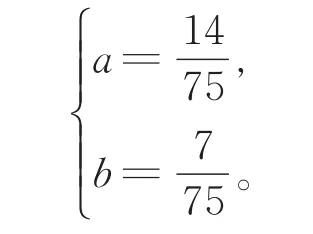
当M=1时,G1的中包含了v(x∅)中的系数
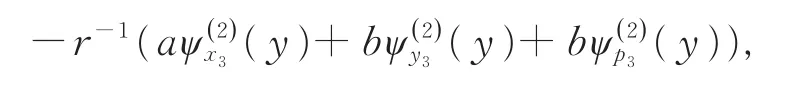
即
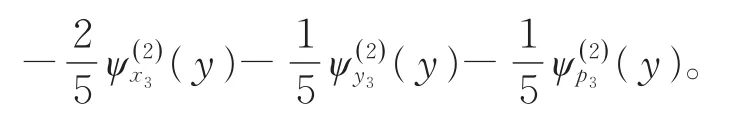
而G1的中含有v(x∅)中的系数
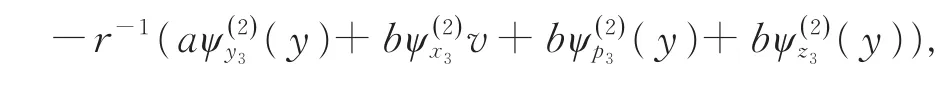
化简得到
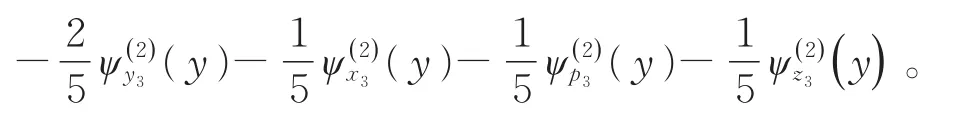
两式相加,得到
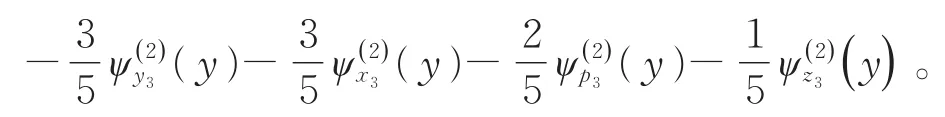
依此类推,就可以得到在此定义域上的格林函数。由此,得到
定理3在SG3的左半定义域Ω中,考虑Dirichlet问题
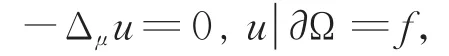
对∂Ω上的任一连续函数,在dom Δμ中都有唯一解,且