几何教学中如何引导学生提升学习的深度

2019-11-04任青

理科爱好者(教育教学版) 2019年4期

关键词：几何教学引导提升

任青

【摘要】“学而不思则罔，思而不学则殆”，没有落到实处的学习效果是肤浅的，两者相结合的方式才能有效地提升学习的深度，达到良好的学习效果。学习的主体是学生，教师是学生学习的引导者，在教学中如何引导学生提升学习的深度，是教师们孜孜不倦的追求。

【关键词】几何教学;引导;提升;学习的深度

【中图分类号】G633.6 【文献标识码】A 【文章编号】1671-8437（2019）22-0186-03

在几何教学中，浮于表面，缺乏深度的学习，会导致不理想的学习效果。笔者结合自身教学经验，从以下几个角度，谈谈在几何教学中教师如何去引导学生提升学习的深度。（文中例题以笔者目前教学中的七下几何题为例）

1 准确审题，把握概念的内涵与外延

中华文字博大精深，在审题中涉及到概念性的词语时，要注意咬文嚼字，关键在于准确理解概念的内涵与外延，注重审题的准确性，提升学习的深度。

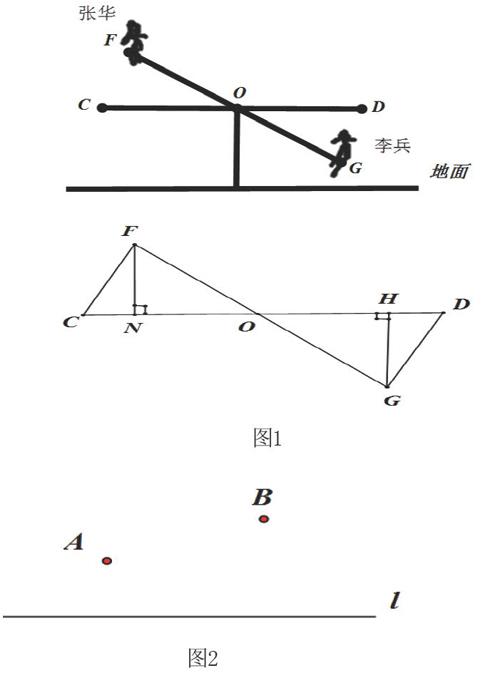
例1 如图1，张华与李兵玩跷跷板游戏。如果跷跷板的支点O（即跷跷板的中点）至地面的距离是60cm，当李兵从水平位置CD下降30cm时，这时张华离地面的高度是____。

1.1 教學反思

平时的教学中发现有的学生解题时读不懂题或者会错了意，这就需要教师在教学中引导学生咬文嚼字，准确理解概念的内涵与外延。

1.2 审题解析

注意引导学生对“距离”、“下降”、“高度”这几个词的准确理解，本质上指的是点到线的距离（点到线的垂线段的长度），尤其是“当小敏从水平位置CD下降30cm时”，这句话中的“下降30cm”，指的是垂线段HG的长度，但学生往往容易理解为斜线段DG的长度！又比如，画一个钝角三角形钝角边的高时，有的学生从小学到初中，就是画不对，究其原因，就是没有从本质上把握三角形某条边的高的定义。为了解决这种概念吃不透的现象，在平时的几何概念教学中，要有意识地引导学生通过动手画图，用数形结合这种直观形象的方式，准确理解和把握几何概念的内涵与外延。

2 深入探究，知其然更要知其所以然

分析解决问题的过程中切忌似懂非懂，要深挖根本原理，理清解法的来龙去脉，从本质上理解并掌握解题方法，提升学习的深度。

例2 如图2，直线l是一条公路，A、B是两个工厂。欲在l上的某处修建一个变电站P，从P向A、B两个工厂铺设电缆，请在图中作出变电站P的位置，使得所需电缆AP+BP的长度最短。

2.1 考点分析

本题考查的是利用轴对称求最短路线问题，熟知“两点之间，线段最短”是解答此题的关键。

2.2 教学反思

本题考查的是轴对称求最短路线问题，在教学中学生可能了解了怎么作图，但对于为什么要这样作图却往往不求甚解，导致一遇到灵活一点的同类题，可能就会束手无策，乱做一气。在教学中，教师在备课中应做好教学预期，并在教学引导上注意深挖细究，采取分解动作、逐层铺垫的方式，让学生从本质上掌握作法的来龙去脉与根本原理。

2.3 教学中采取逐层铺垫方式

（1）填空：两点之间，____最短。图3中，A′、B两点之间，____最短。

（2）如图3，欲在直线l上的某处修建一个变电站P，向A′、B两个工厂供电，作出变电站P的位置，使所需电缆A′P+BP的长度最短。

分析：因为A′、B两点之间____最短，所以连接A′、B交直线l于点P（如图4），则点P即为所求点。

（3）说说轴对称的性质。请在图2中作出点A′关于直线l的对称点A，线段AP与A′P有何位置与数量关系？

（4）回到本题，你会解决了吗？（学生独立思考后可小组内交流讨论，然后尝试自主作图）请说出你的解题依据和作图步骤。

解法：如图5，作点A关于直线l的对称点A′，连接A′B交直线l于点P，则点P即为所求点。

（5）如图6，当变电站建在直线l上其它位置（如P′）时，求证此时必有AP′+BP′>AP+BP

证明：∵点A与A′关于直线L对称，∴AP=A′P，AP′=A′P′，

∴AP+BP=A′B，AP′+BP′=A′P′+BP′，在△A′P′B中，∵A′P′+BP′>A′B

∴AP′+BP′>AP+BP，故点P为最佳位置。

本人在教学中通过以上五个步骤，层层铺垫，引导学生从本质上掌握解法的来龙去脉与根本原理，能够有效引导学生知其然更要知其所以然。

3 合理联想，寻找解题的突破口

利用已知条件或结论进行恰当的知识点与解法的合理联想，寻找解题的突破口促进顺向或逆向思维发展，提升学习的深度。

例3 如图7，已知∠A=∠D=90°，E是AD的中点，CE平分∠DCB。求证：（1）BE平分∠ABC;（2）BE⊥CE。

问题解析：

方法1：（执因索果）由已知CE平分∠DCB，∠D=90°，联想到角平分线的性质定理，过点E作EN⊥BC，垂足为N，先说明EN=DE，再说明EN=EA，由角平分线的判定定理证得BE平分∠ABC;再利用两直线平行同旁内角互补可得∠2+∠3=90°，故∠BEC=90°，得证BE⊥CE。

方法2：（执果索因）从要证的结论出发逆向思维，联想到“三线合一”，那么线段BE应该是某个等腰三角形底边上的中线，由解题模型“平行线加角平分线可证得等腰三角形”，故延长CE与BA，交于点F，证得BC=BF，再证△DCE≌△AFE（ASA），得CE=EF，由等腰三角形三线合一，得证BE平分∠ABC且BE⊥CE。

特别地，执果索因这种逆向思维方式在几何题的证明中卓有成效，有助于快而准地破题。

4 化繁为简，对图形进行合理的分解与组装

对于复杂的图形，仔细观察分析，学会抽丝剥茧，善于从复杂图形中分解出基本图形，用基本图形蕴含的规律解决复杂图形的问题，培养学生对问题的分解与组合的能力，提升学习的深度。

例4 如图8，BE、CF分别平分∠ABD与∠ACD，BE与CF交于G，若∠BDC=130°，∠BGC=100°，求∠A的大小。

问题解析：

本题解法不唯一，这里介绍一种引导学生对复杂图形作解剖，从复杂图形中分解出基本图形，用基本图形蕴含的规律去解决复杂图形问题的方法。

（1）探究基本图形中∠1、∠2、∠3、∠4的数量

关系：

（2）拆分图形，按规律计算：

图9中，∠BDC=∠BGC+∠GBC+∠GCD，130°=100°+∠GBD+∠GCD，得∠GBD+∠GCD=30°，由BE是∠ABD的平分线.CF是∠ACD的平分线，得∠ABD+∠ACD=2（∠GBD+∠GCD）=60°

图10中，∠BDC=∠A+∠ABD+∠ACD=∠A+60°，130°=∠A+60°，故∠A=70°

在几何教学中，应多多训练学生对复杂的图形进行合理的分解与组装，提高识图、解图的能力。