胡爱莲

(喀什大学 数学与统计学院，新疆 喀什 844006)

1 引言和主要定理

本文考虑如下的Kirchhoff方程：

(1)

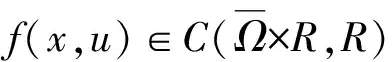
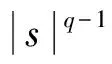
(2)

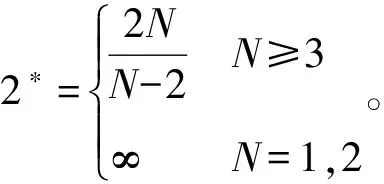
文献[1-8]对Kirchhoff方程的Dirichlet问题进行了研究，文献[2-3]在Ambrosetti-Rabinowitz条件(简记为(AR)条件)下得到了这类问题解的存在性。这里(AR)条件如下：

(AR)条件可以保证问题(1)对应的能量泛函的所有(PS)序列有界，从而保证了变分方法的应用。但很多超线性函数并不满足(AR)条件。本文利用喷泉定理，在比(AR)条件更弱的一类超线性条件之下，得到了问题(1)无穷多个大能量解的存在性，主要结果如下：

定理1设f(x,u)∈C(Ω×R,R)，且满足式(2)及以下条件：

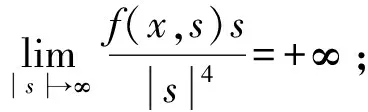
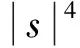
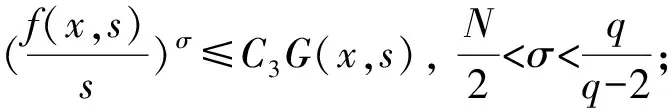
(f4)对(x,t)∈Ω×R，有f(x,-t)=-f(x,t)，则问题(1)存在一列解{uk}k∈Ν满足：k→+∞时，

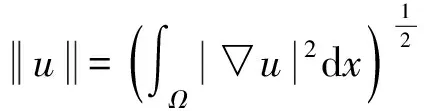
2 Cerami条件和喷泉定理

对于问题(1)，考虑泛函I:H1(Ω)→R，

(3)

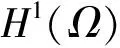
(4)

定义1设X是Banach空间，称泛函J∈C1(X,R)满足Cerami条件，如果对任何的{un}⊂X,由J(un)→c,(1+||un||)J′(un)→0(n→∞)，可推得{un}存在收敛的子列。

要证明定理1，需用到如下的临界点定理——Bartsch喷泉定理。

命题1[9]设X是可分的Banach空间，于是存在{vn}n∈Ν⊂X,{φn}n∈Ν⊂X*，使得

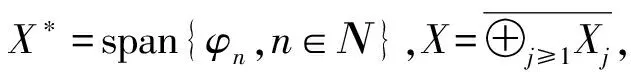
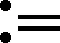
注1在文献[9]中，喷泉定理是在(PS)条件下得到的，虽然Cerami条件比(PS)条件弱，但和(PS)条件一样，Cerami条件足以保证(第一)形变定理的成立(见文献[10]),所以可以在Cerami条件下得到喷泉定理。

引理1设f(x,u)满足式(2)以及条件(f1)、(f2)和(f3)，则泛函I(u)满足Cerami条件。

则存在C4>0，使得

||I(un)||≤C4，(1+||un||)||I′(un)||≤C4

(5)

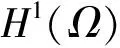
由条件(f2)可知，存在常数C5>0，使得

(6)

对所有s∈R,x∈Ω。

由式(3)～(6)可得

(7)

于是存在常数C6>0，使得

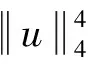
(8)

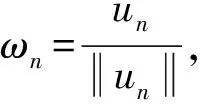
(9)

由内插不等式及式(9)，有

(10)

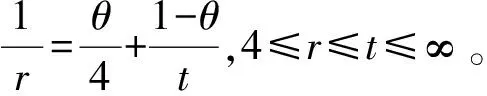
由式(4)可得

当||un||→∞(n→∞)，由式(5)，当n充分大时，有

(11)

由条件(f3)及式(7)，可得

(12)

由积分绝对值不等式、Holder不等式、式(10)(12)有

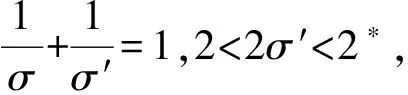
3 定理1的证明

由条件(f4)可知，I(-u)=I(u)，由引理1，泛函I(u)满足Cerami条件，要证明定理1，下面只需证明I(u)满足命题1中的条件即可。

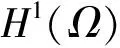
由式(2)知，存在常数C8>0，使得

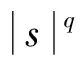
(13)

于是对u∈Zk，由式(3)(13)有

2)因dimYn<+∞，由有限维空间上各种范数等价，故存在C9>0，对任u∈Yk，有

(14)

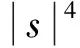
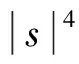
(15)

由式(14)(15)知，对任u∈Yk，||u||充分大时，有

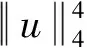
由此可见，对充分大的ρk>rk>0，有

由命题1知，泛函I(u)有一列临界点{uk}k∈Ν，使得I(uk)→∞(k→+∞)。

定理1证毕。

注2下面说明条件(AR)比条件(f1)、(f2)和(f3)要强。

事实上，由(AR)条件，有

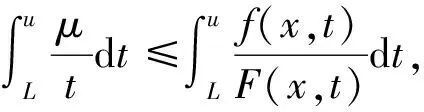
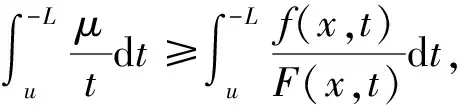
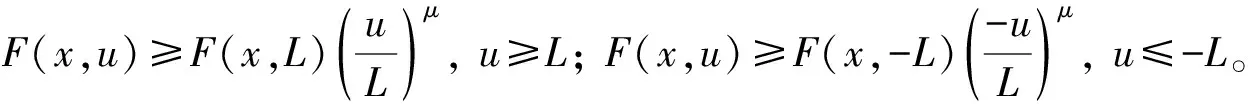
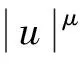
(16)

即(f1)成立。

由式(2)有

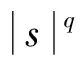
(17)

(18)

由(AR)条件，得

(19)

再由式(18)(19)，可得存在C3>0，使得

即条件(f3)成立。