魏峰 金亮† 柳军 丁峰 郑新萍

1)(国防科技大学空天科学学院,长沙 410073)

2)(国防科技大学计算机学院,长沙 410073)

1 引 言

在计算流体力学领域,笛卡尔网格相比贴体网格有着高效率、高鲁棒性、高灵活性等突出优势,能够很好地应对复杂的流动问题[1,2].作为笛卡尔网格技术的关键,物面处理的方式一直是国内外学者们研究的热点,近年来,浸入边界法(immersed boundary method)[3]越来越受到研究者们的重视,这种方法相比切割单元法(cut-cell method)[4]不需要对网格进行切割,极大地减小了计算量,在模拟包含运动边界的流动问题时有着明显的优势.常规的浸入边界法包括连续力法和离散力法,这两种方法在模拟不可压缩流的领域都获得了极大的成功[5,6],然而在模拟高雷诺数情况下的可压缩流动时都存在着很大的误差.为了弥补这一缺陷,Majumdar等[7]提出了虚拟单元法(ghost cell method),即在物体内部构建虚拟流场,通过对虚拟流场内的虚拟单元进行合理的赋值,隐式地表达物面边界条件.一般情况下,虚拟单元定义为周围至少存在一个流场单元的物体内部单元,但是对于一些高阶的虚拟单元法,则需要扩展更多的虚拟单元[8],对于存在细长结构的几何模型,虚拟单元还可以定义在流场内部[9].虚拟单元法以其灵活简单、鲁棒性好等优点得到了众多学者的关注.Tseng和Ferziger[10]对浸入边界虚拟单元法在各种边界条件下的应用进行了系统的研究;Dadone和Grossman[11],Farooq等[12]以及Chi等[13]都对可压缩流动中的虚拟单元法进行了详细研究并发展了各自的虚拟单元法.

对于含有运动边界的复杂流动问题,早期的物面边界处理方式为切割单元法,容易导致所谓的“细小网格”问题,严重限制了时间步长.为了避免这一问题,Mittal 和Iaccarino[5]将细小的切割单元与周围的流场单元进行融合以消除细小单元,Forrer 和Berger[14]借鉴了浸入边界法的思想,将切割单元进行了填充并且设置了一系列的虚拟单元,两者都成功地求解了含有运动边界的流动问题.Lee 等分析研究了求解运动边界问题时产生的压力振荡,通过实验发现减小网格尺寸或者增大时间步长都可以减小压力振荡[15],进而提出了一种能够有效地控制压力振荡的隐式浸入边界虚拟单元法[16].Tan和Shu[8]推导了一种复杂的能够处理运动边界问题的高阶虚拟单元法,通过有限差分的方法分别求解了一维算例和二维算例,其精度分别达到了四阶和三阶.Peter和De[17]在非惯性系下对GCIBM (ghost-cell immersed boundary method)方法进行了拓展,同时能够实现并行求解,相比在惯性系下求解包含运动边界的流动问题,避免了压力的数值振荡,但是也存在着无法模拟多体相对运动的局限性.在国内,赵宁等[18,19]在自适应笛卡尔网格的基础上对虚拟单元法进行了大量的研究,同时也对包含运动边界的情况进行了数值模拟.

在文献[12]提出的SGCM (simplified ghost cell method)基础上,本文提出了一种改进的虚拟单元法,同样使用了流场点作为镜像点,但是相比之下具有更高的准确性和计算效率.考虑到物面边界变速运动会导致边界附近的压力、密度和切向速度存在梯度,给出了改进型虚拟单元法的推广形式,用于求解包含运动边界的流动问题.通过求解Schardin问题和激波抬升轻质圆柱问题验证了该虚拟单元法及其推广形式在处理包含静止/运动边界的流动问题时的准确性.本文第2节简要介绍了求解过程中使用的控制方程以及空间、时间离散格式,进而详细介绍了改进的虚拟单元法及其推广;第3节给出了两种经典的流动问题的计算结果和讨论;第4节给出了结论.

2 数值方法

2.1 控制方程

二维无黏可压缩欧拉方程的有限体积形式如下[20]：

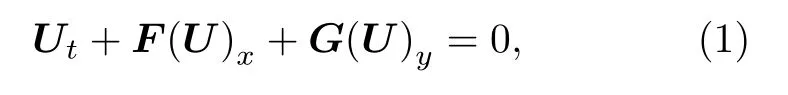
其中,

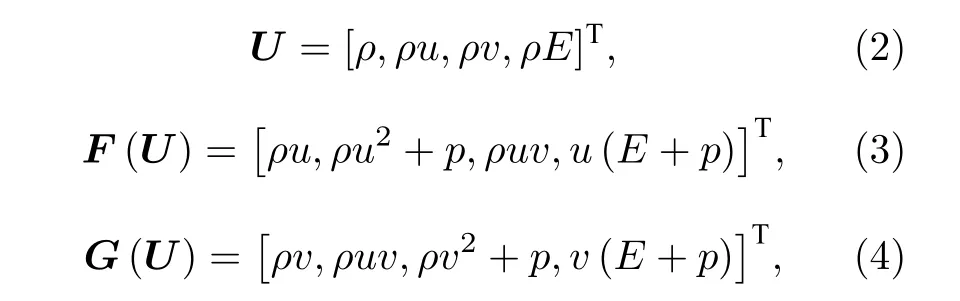
U为守恒变量;F(U)和G(U)分别为X和Y方向上的通量;ρ为密度;u和v分别为沿X和Y方向的速度分量;p为压强;E为总能.考虑到气体的热力学性质,补充方程(5)封闭上述方程系统,

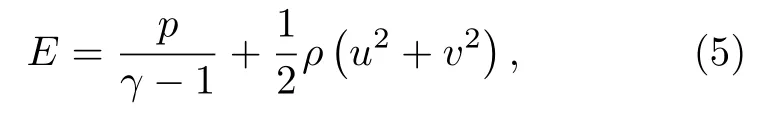
其中比热比γ取1.4.

2.2 离散

采用AUSM + (advection upstream splitting method +)格式计算对流通量[21],为了提高计算精度,通过MUSCL (monotonic upstream-centered scheme for conservation laws)方法[22]在单元交界处采用二阶精度重构格式对变量进行重构,同时选用MINMOD限制器限制重构时使用的梯度,防止重构格式出现振荡.

时间离散采用显式三阶TVD (total-variationdiminishing)Runge-Kutta格式[23],具体形式如下：

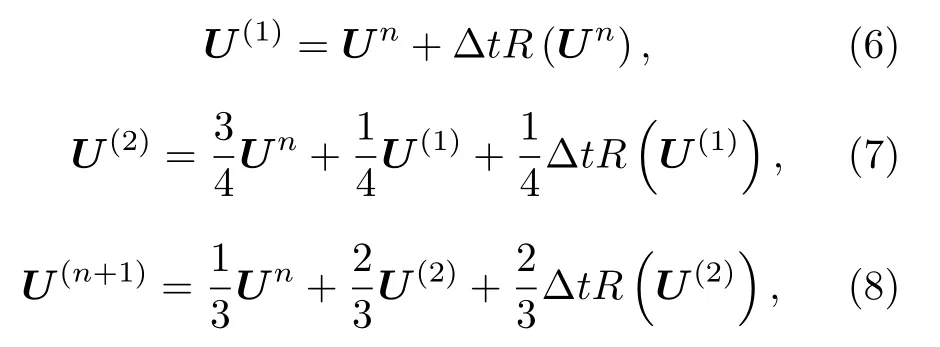
其中R(*)为残值,Δt为时间步长.对于非定常问题,应采用全场统一时间步长,全场统一时间步长是所有当地时间步长的最小值,即

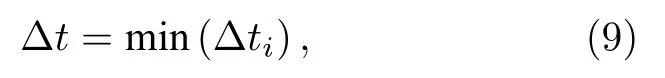
式中Δti为当地时间步长.

2.3 改进的虚拟单元法

在使用常规的虚拟单元法求解可压缩流动问题时,通常需要得到虚拟单元关于物面的镜像点,然后通过插值得到镜像点的变量值,进而求得虚拟单元的变量值.一般情况下,镜像点周围都有着足够的插值点,因此能够采用各种插值方法得到比较准确的数值,但是对于图1中出现的情况,物体底部虚拟单元的镜像点缺乏合适的插值点,因此需要进行特殊的处理.一般地,可以将距离镜像点最近流场点的变量值赋给镜像点,或者是距离虚拟单元最近流场点的变量值赋给镜像点.然而,这种近似的赋值方式会引入一定的误差,对于误差存在积累效应的非定常问题,如果一开始就存在较大的误差将严重影响最终结果的准确性.

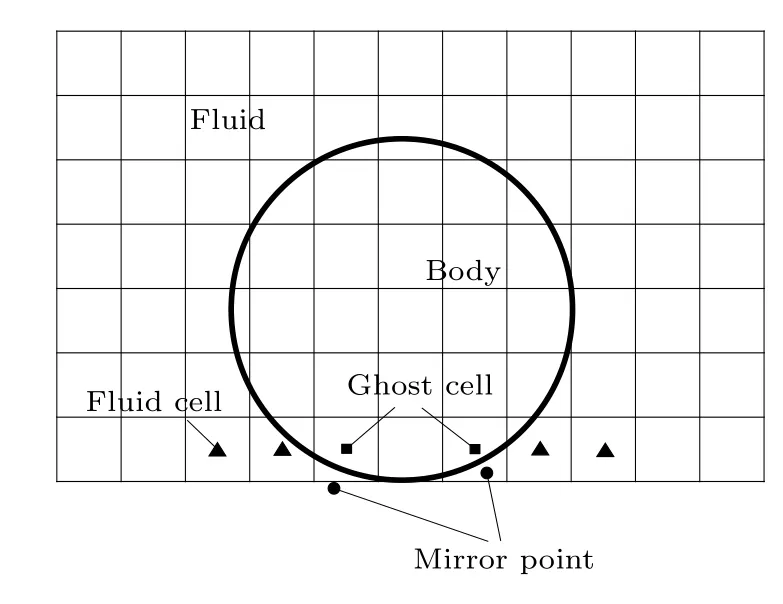
图1 狭缝问题(物体底部虚拟单元的镜像点缺乏合适的插值点)Fig.1.Slit problem,which is caused by the lack of interpolation points of the mirror points.

为了不采用这种近似的处理方法,与Farooq等[12]在2013年提出的SGCM相似,选择了X或者Y方向的流场点代替了镜像点,避免了插值运算,因此能够很好地处理狭缝问题.考虑到镜像点与物面点十分接近时,速度赋值公式存在分母接近0的情况而产生非物理解,在SGCM中假设了物面点位于虚拟单元和镜像点中间,但同时也引入了一定的误差.如图2所示,使用了精确的物面点位置求得虚拟单元的变量值,从而能够精确地表达物面边界,同时为了保证方法的稳定性,在计算过程设定当镜像点与物面点距离小于0.2个网格单元长度时,就要取镜像点向外延伸后的第二个流场点作为镜像点,例如,图2中虚拟单元B的镜像点本来应该是流场点N,但是由于N点与物面点MB的距离过近而选择了N点上方的流场点FB.值得注意的是,对于这种改进的虚拟单元法,如果虚拟单元距离在X方向或者Y方向上的镜像点过远,则将只考虑距离虚拟单元最近的镜像点,例如图中的虚拟单元B沿X方向的第一个镜像点为流场点,这两点的距离达到了3倍的网格长度,因此在对虚拟单元B赋值时只需考虑其沿Y方向的镜像点即可,在实际计算时,当虚拟单元与第一个镜像点之间距离为1到2个网格长度时需要考虑两个方向的镜像点,如虚拟单元A和C.对于非曲面物面,虚拟单元的赋值方法如下所示：

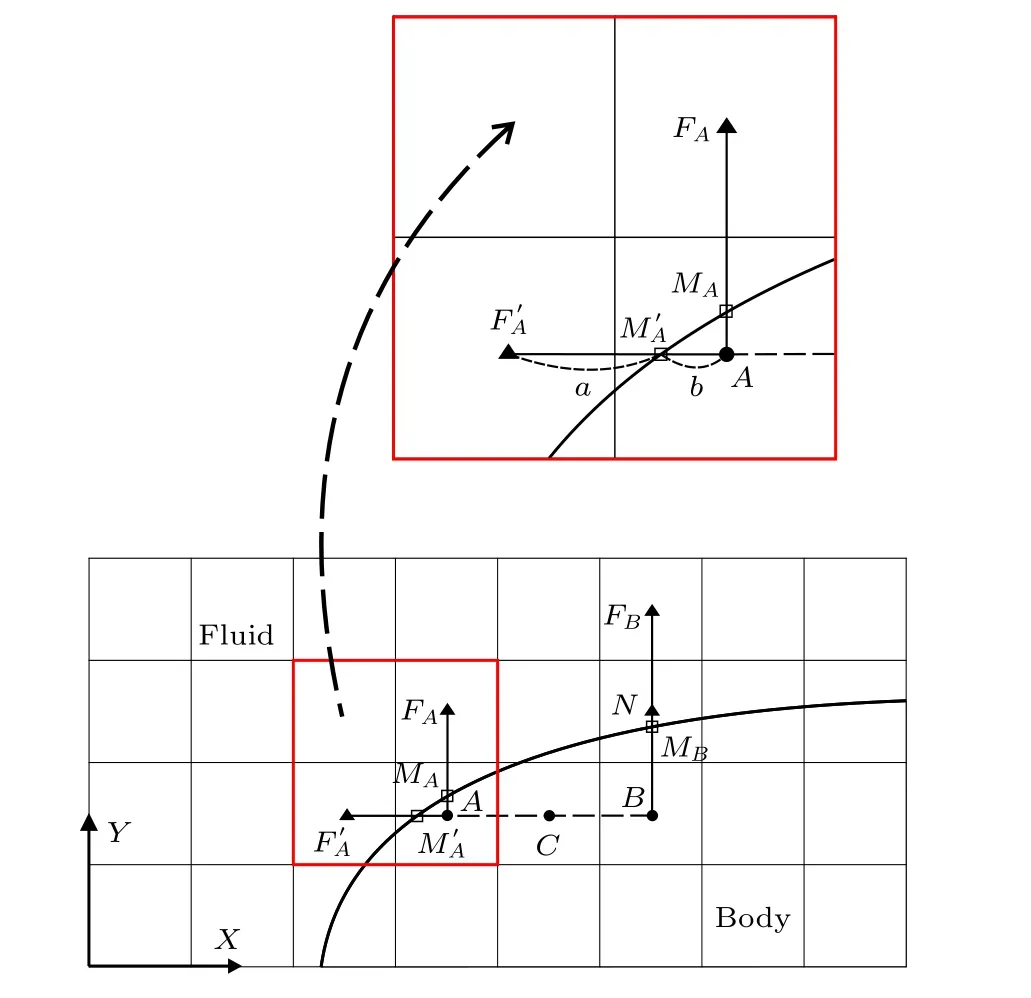
图2 改进的虚拟单元法示意图Fig.2.Demonstration of the improved ghost cell method.

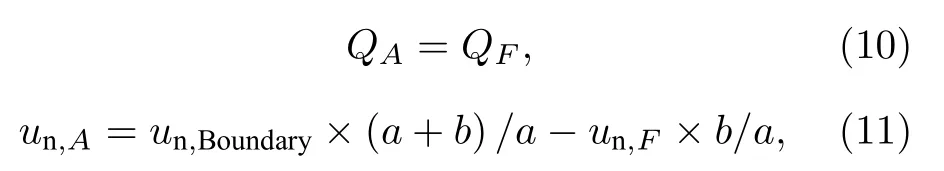
其中Q代表压强p、密度ρ以及沿着物面的切向速度ut;un代表物面法向速度;a和b分别代表镜像点到物面点的距离和虚拟单元到镜像点的距离.对于曲面物面,在计算除un以外的其他变量时不能忽略曲率半径的影响,因此在计算这些变量时需要对(10)式进行修改,本文采用了与文献[12]相同的压力赋值公式.在SGCM中,镜像点的选择(X方向上选择或者Y方向上选择)依据物面的法向向量,因此在镜像点选择更替的区域,流场变量会可能出现不连续,如图3所示,在使用SGCM方法计算超声速圆柱绕流时,在r/R=0.7附近的压力系数会出现扭曲现象.为了解决这个问题,Farooq等[12]在镜像点的选择中增加了斜上(下)方的流场点,得到了MSGCM (modified simplified ghost cell method),消除了扭曲,但是使得代码中的判断语句变得非常多.我们则根据距离加权的方式来光滑变量值,即同时得到X方向以及Y方向的镜像点,通过(10)和(11)式分别求出相应的虚拟单元变量值,最终的虚拟单元变量值根据它们距离物面的长短进行加权,这一过程并没有引入过多的判断语句.在相同的设置参数和网格量下我们求解了文献[12]中的超声速圆柱绕流算例,计算结果如图3所示,可以看出本文发展的改进型虚拟单元法(ISGCM)同样能够消除计算过程中出现的扭曲现象,并且比SGCM和MSGCM更加精确.

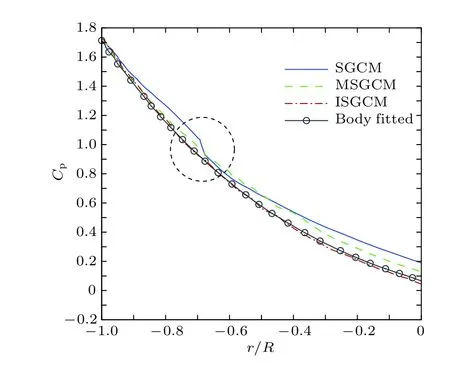
图3 SGCM中出现的扭曲现象(标记区域)以及采用ISGCM求得的圆柱表面压力系数与采用SGCM、MSGCM、贴体网格得到的结果的对比Fig.3.Kink noted in the picture,which is happened when using the SGCM,and the comparison of the pressure coefficients obtained by using SGCM,MSGCM,ISGCM and the body fitted mesh.

2.4 推广的改进型虚拟单元法

对于变速度的运动边界问题,边界附近存在着压力、密度和切向速度的梯度[12],因此在计算虚拟单元的变量值时我们额外选取了一层镜像点(图4),增加了FA,2,以及FB,2,结合对应的第一层镜像点FA,1,和FB,1得到近壁面的变量梯度,进而求解虚拟单元的变量值.(12)和(13)式给出了这种推广形式的虚拟单元赋值方法：

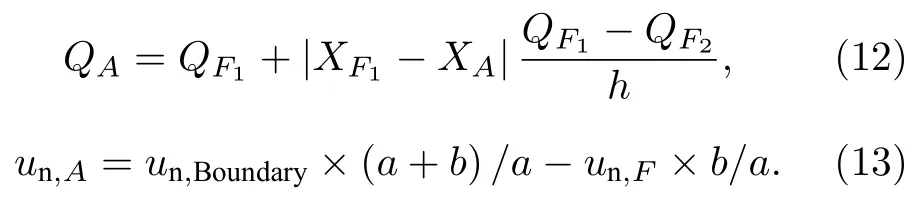
在对虚拟单元赋值时,除了上文中提到的特殊情况,都需要分别得到沿X和Y方向求得的虚拟单元变量值,再根据虚拟单元与物面点之间的距离进行加权.当物面附近存在激波时,例如一道激波介于流场点FA,1和FA,2之间,采用(12)式得到的压力等变量会出现很大或者很小的数值,甚至出现负值,导致计算发散.因此我们增加了一个激波监测器α,用来检测FA,1和FA,2之间是否激波,其定义如下：

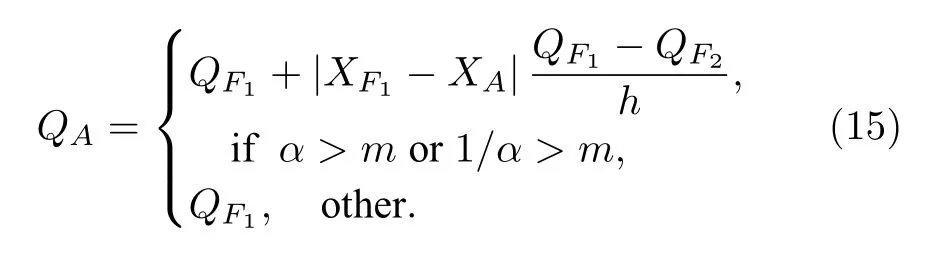
图4 推广的改进型虚拟单元法示意图Fig.4.The demonstration of the extended ISGCM.

3 计算结果与讨论

为了验证本文发展的改进型虚拟单元法,首先求解了Schardin问题,并与相关文献进行对比,验证了方法在求解包含静止边界的非定常流动问题时的准确性,进而求解了存在狭缝问题的激波抬升轻质圆柱问题,通过和相关文献进行对比,验证了在包含运动边界情况下方法的准确性以及对狭缝问题的处理效果.

3.1 Schardin问题

Schardin问题于1957年由Schardin提出[24],此后,一些学者对该问题进行了实验和数值模拟,本算例选用了Chang等[25]提出的研究模型,模型描述如图5所示,初始时刻(T=0),距离左边界50 mm处有一道激波,随着时间的推移,激波将以Ma=1.34向后扫过一个夹角约为60°的三角楔,流动过程中将出现马赫杆、三波点、滑移线、膨胀波等复杂的流场结构,初始时低压区的静压为0.05 MPa,更多的细节可以查看文献[25].左边界赋值为波后条件,右边界以及上下边界为超声速出口条件,物面边界采用本文发展的ISGCM,计算网格采用了均匀的笛卡尔网格,分别计算了网格量大小为142×100,426×300和710×500时的流动情况.

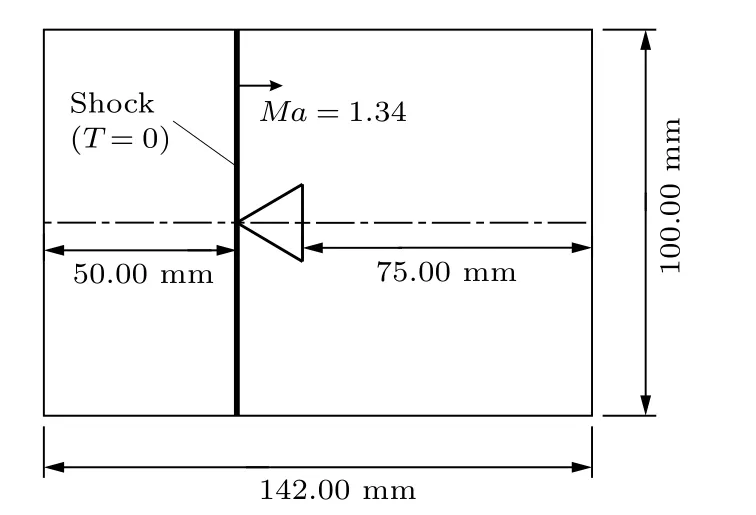
图5 Chang等[25]用来研究Schardin问题的物理模型Fig.5.Physical model of the Schardin's problem proposed by Chang et al.[25].

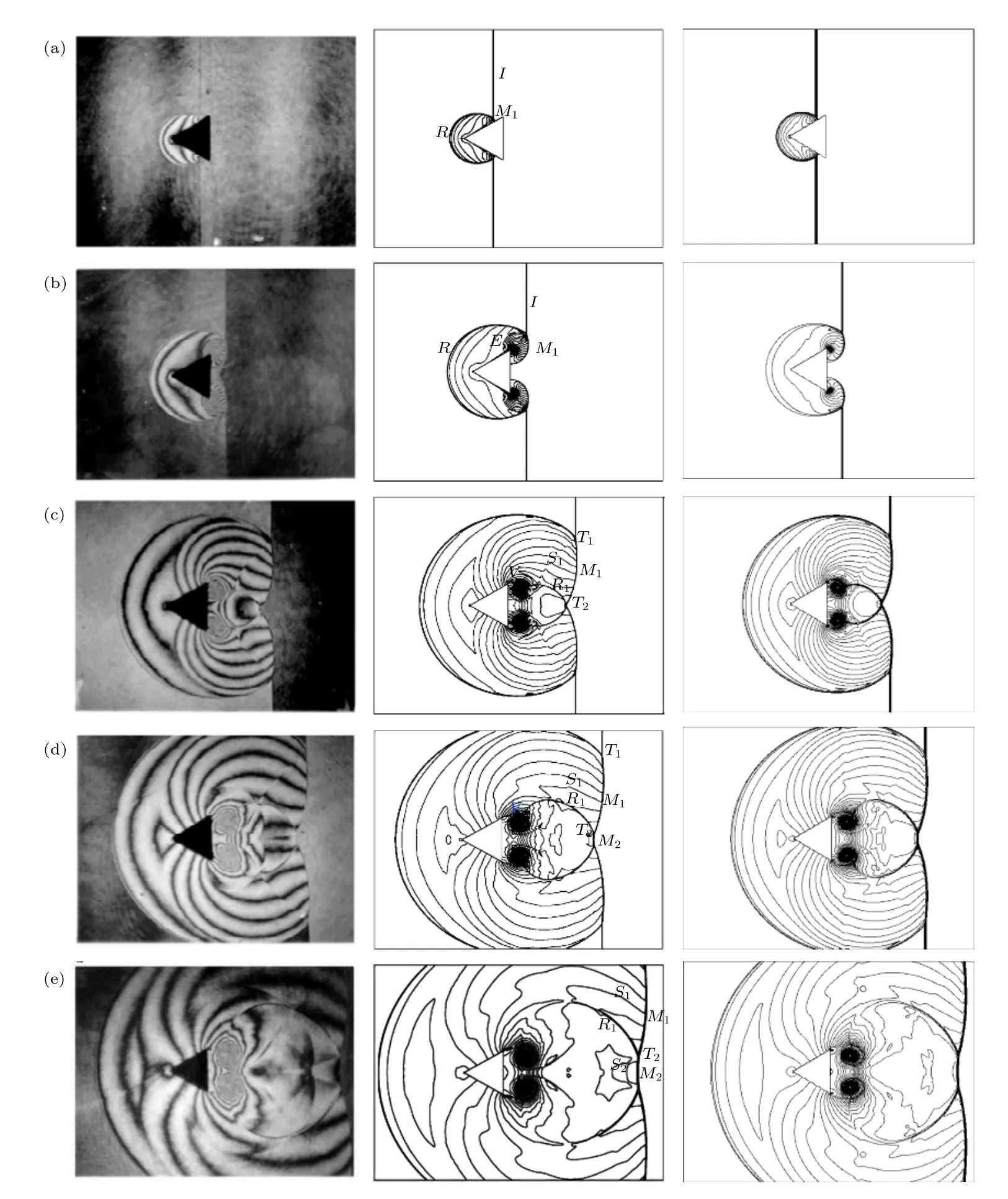
图6 不同时刻下的实验结果(左)、Chang等[25]计算所得的密度等值线(中)和采用ISGCM计算所得的密度等值线(右)(a)T=28 μs;(b)T=53 μs;(c)T=102 μs;(d)T=130 μs;(e)T=172 μsFig.6.Experimental results (left),Chang et al.[25] results and the density contour computed by us (right)：(a)T=28 μs;(b)T=53 μs;(c)T=102 μs;(d)T=130 μs;(e)T=172 μs.

图6分别给出了在网格量大小为710×500时采用ISGCM所得的密度等值线图(右)、Chang等[25]使用数值计算得到的密度等值线图(中)以及通过双脉冲全息干涉法得到的T=28,53,102,130,172 μs时的实验结果(左),其中文献[25]在数值计算过程中在自适应的四边形贴体网格上使用MUSCL方法得到了二阶精度的计算结果.图7(a)给出了不同网格量下计算所得的沿模型中间对称线上的密度分布与文献[25]的数值计算结果以及部分实验数据的对比,图7(b)给出了不同网格量下计算所得的沿模型中间对称线上的马赫数分布与文献[25]的数值计算结果的对比.可以看出,计算结果与文献[25]的实验以及计算结果基本一致,表明本文所发展的改进型虚拟单元法能够达到与贴体网格相同的精度.

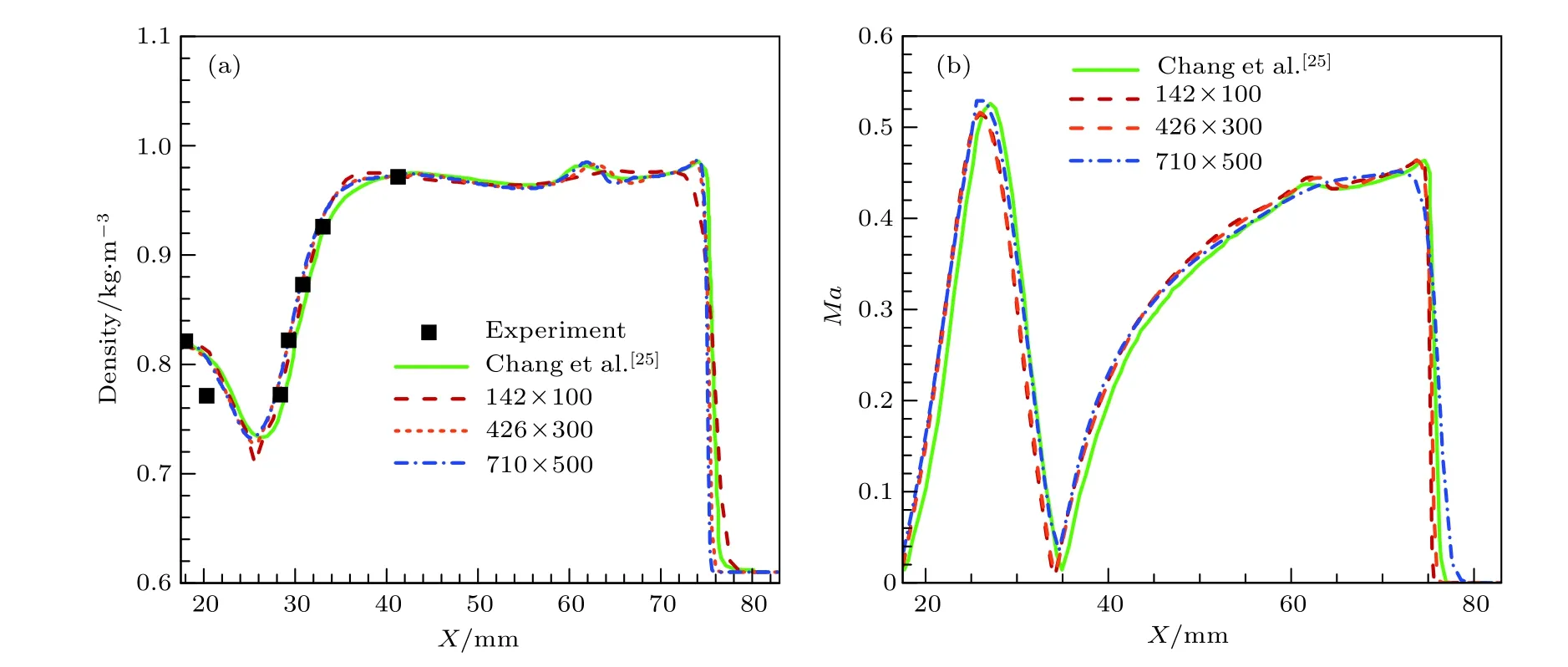
图7 (a)计算所得沿模型中间对称面上的密度分布与Chang等[25]的计算结果以及实验数据的对比;(b)沿模型中间对称面上的马赫数分布与Chang等[25]的计算结果的对比Fig.7.(a)Comparison of the density distribution along the symmetry plane between the results obtained by this paper and Chang et al.[25] as well as the experiment;(b)the comparison of the Mach number distribution along the symmetry plane between the results obtained by this paper and the results of Chang et al.[25].

3.2 激波抬升轻质圆柱

在此算例中,一道激波从左至右传播,一个刚性轻质圆柱放置在管道内,当激波接触圆柱后,会对圆柱产生作用力并将其抬升,文献[8,14,26]都求解了该问题并进行了分析.本文采用文献[8]的计算模型,模型示意图见图8,计算域的大小为[0,1]×[0,0.2],刚性轻质圆柱的半径为0.05,密度为10.77.初始时刻,圆柱中心点的位置为(0.15,0.05),一道激波在X=0.08处,并以马赫数Ma=3的速度朝着X的正方向传播.左边界设置为波后条件,右边界为超声速出口边界,上下边界均为固壁.初始流场中低压区的静压为1.0,密度为1.4.

上下边界采用了对称反射边界条件,物面边界采用了ISGCM的推广形式.初始时刻,圆柱刚好与计算域的下边界接触,形成狭缝问题,设定在计算距离下边界很近的虚拟单元变量值时只考虑X方向的镜像点.值得注意的是,这里并没有引入对镜像点的近似赋值,仍然是对物面边界的精确表达.表1列出了不同网格量下T=0.1641和0.30085时圆柱中心的坐标,计算结果与文献[8]符合得较好.图9和图10分别给出了网格量为600×120时计算所得T=0.1641和0.30085时的压力等值线图(a)和网格量为640×128时文献[8]的计算结果(b),其中文献[8]在计算过程中使用了复杂的三阶精度虚拟单元法.可以看出计算结果基本吻合,表明推广的改进型虚拟单元法能够用于求解包含运动边界的流动问题.

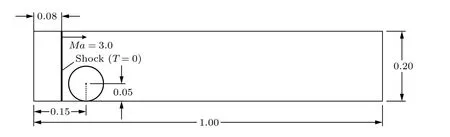
图8 激波抬升轻质圆柱问题的模型描述Fig.8.Physical model of the cylinder lift-off problem.

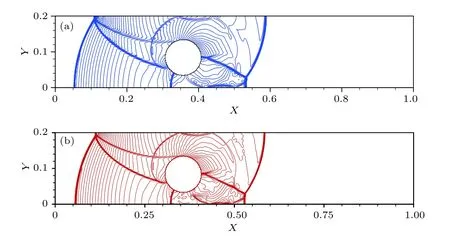
图9 T=0.1641时的压力等值线图 (a)本文所推广的改进型虚拟单元法(网格量为600×120);(b)Tan等[8]使用的高阶虚拟单元法(网格量为640×128)Fig.9.Pressure contour atT=0.1641：(a)Extended ISGCM with the grid size of 600×120;(b)high-order ghost cell method proposed by Tan et al.[8] with the grid size of 640×128.

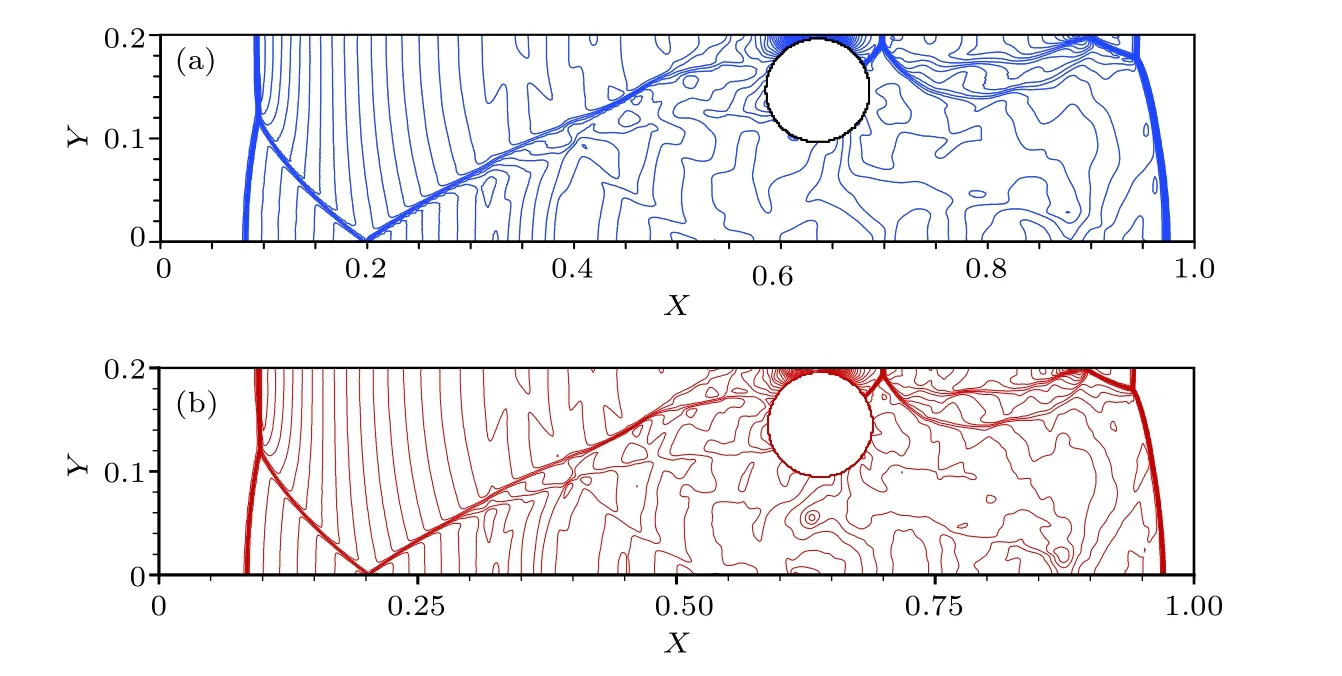
图10 T=0.30085时的压力等值线图 (a)本文所推广的改进型虚拟单元法(网格量为600×120);(b)Tan等[8]使用的高阶虚拟单元法(网格量为640×128)Fig.10.Pressure contour atT=0.30085：(a)Extended ISGCM with the grid size of 600×120;(b)high-order ghost cell method proposed by Tan et al.[8] with the grid size of 640×128.

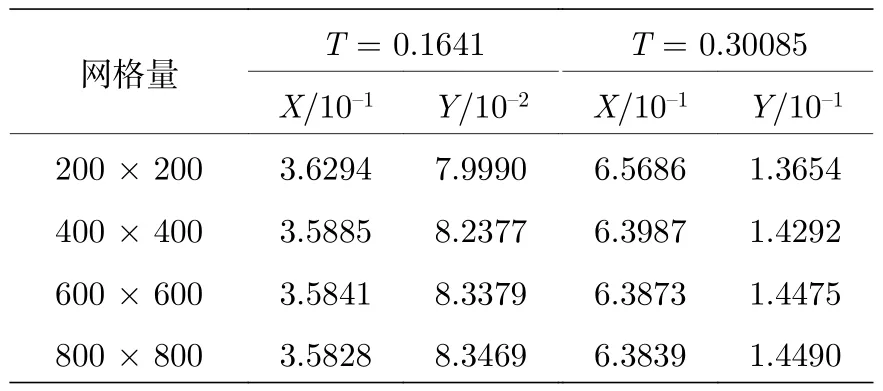
表1 不同网格量下T=0.1641和0.30085时圆柱中心的坐标Table 1.Position of the center of the cylinder atT=0.1641 and 0.30085.

4 结 论

本文提出了一种改进的虚拟单元法求解包含静止和运动边界的流动问题.在该方法中,虚拟单元的镜像点用沿X和Y方向的流场点代替,虚拟单元的最终值通过其沿X和Y方向得到的变量值按照距离长短加权得到.考虑到物面边界变速运动时不能忽略近壁面处的变量梯度,我们对该虚拟单元法进行了推广,增加了一层镜像点,使其能够处理包含变速运动边界的流动问题,同时为了避免激波贴体时产生非物理解,加入了激波监视器,提高了方法的稳定性.最后通过求解Schardin问题和激波抬升轻质圆柱两个经典算例验证了方法的可靠性和准确性.本文的结论如下：

1)与传统的虚拟单元法相比,本文的方法不需要插值得到镜像点的变量值,保持了笛卡尔网格的简单性,减少了计算量,同时由于镜像点就是流场点,因而能够很好地处理狭缝问题;

2)与SGCM相比,本文的方法使用了精确的物面点求解虚拟单元的变量值,能够准确地表达物面边界条件,并且不存在扭曲现象,同时还避免了过多判断语句的引入,具有更高的准确性和计算效率;

3)通过求解Schardin问题验证了本文的方法可以较好地处理包含静止边界的流动问题,同时能够达到与贴体网格相同的精度;通过求解激波抬升轻质圆柱问题,并与复杂的高阶虚拟单元法进行对比,验证了本文相对简单的虚拟单元法能够满足处理包含运动边界问题的要求.

感谢上海航天科技创新基金提供的资金支持,同时衷心感谢审稿人的建设性意见和建议.