广东省佛山市南海区黄岐高级中学

熊向前 (邮编：528248)

广东省广州市广东华侨中学

杨 墁 (邮编：510000)

在看完2018年全国I卷理科数学第19题后,现从不同角度对其解法进行了探究,并将其结论拓展推广到其他的圆锥曲线中,在追溯其命题背景之后,又发现了其结论更为一般的形式.现整理成文,不当之处,敬请批评指正.

1 试题呈现

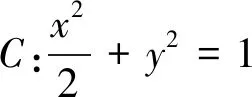
(1)当l与x轴垂直时,求直线AM的方程;

(2)设O为坐标原点,证明:∠OMA=∠OMB.(2018年全国I卷理科数学第19题)

评注本题考查椭圆的标准方程及其几何性质、直线的方程、直线与椭圆的位置关系、斜率、韦达定理、等角的证明等基础知识,考查学生的推理论证能力、运算求解能力以及综合运用所学知识分析问题和解决问题的能力,考查数形结合的思想、分类讨论的思想、化归与转化的思想.立意深刻、内涵丰富,具有一定的典型性、代表性,极具探究价值,是一道值得研究的好题.

2 解法探究

破解此题的关键:一是画图引路,先画出大致图形,把题中的数学符号语言翻译成图形语言;二是合理转化,以数助形,把几何关系等价转换其他的数量关系.

证法1当设直线AB与x轴重合时,显然成立;

当设直线AB与x轴不重合时,由题意F(1,0),设直线AB的方程为x=my+1,A(x1,y1),B(x2,y2),将x=my+1代入椭圆C的方程，得(m2+2)y2+2my-1=0,则

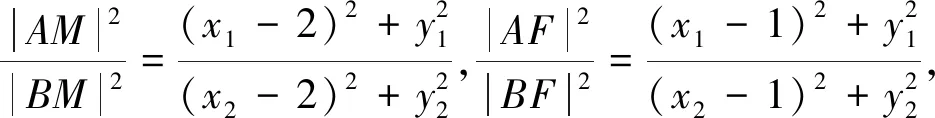
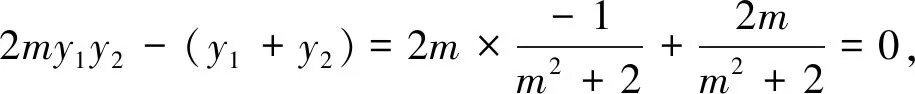
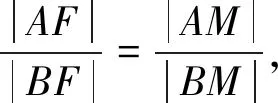
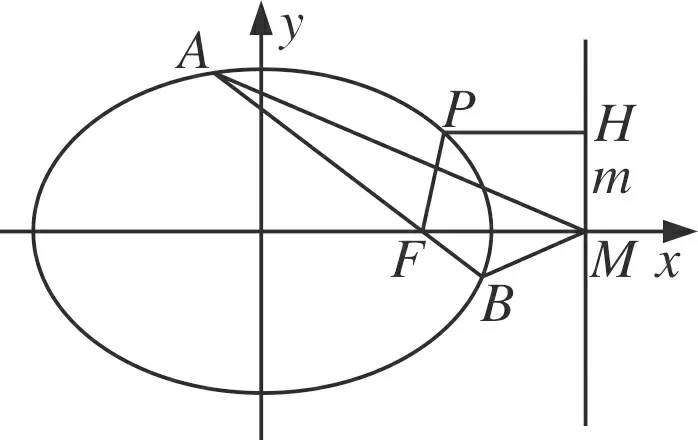
图1

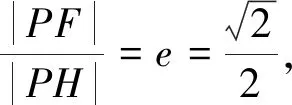
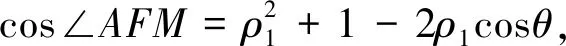
下同证法1.

证法3设直线l的参数方程为

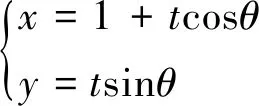
A(1+t1cosθ,t1sinθ),B(1+t2cosθ,t2sinθ),

将(*)代入椭圆C的方程得

(sin2θ+1)t2+2tcosθ-1=0,则

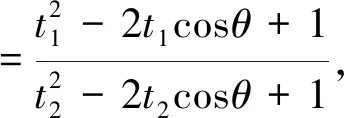
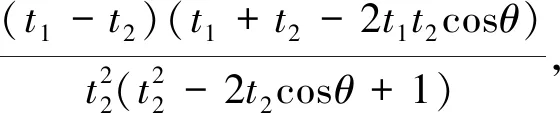
证法4 由证法1知

而2my1y2-(y1+y2)=0,所以kAM+kBM=0,从而得直线AM与直线BM的倾斜角互补,所以∠AMO=∠BMO.

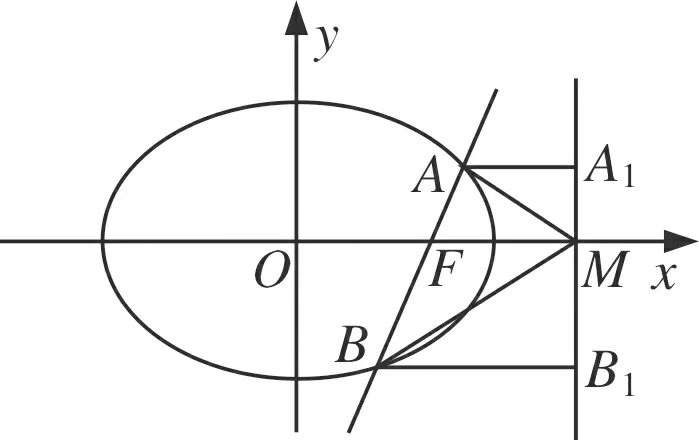
图2

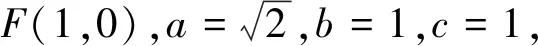
评注在以上方法中,前三种方法均借助于三角形内角平分线定理,把要证明的角的关系转化成线段间的数量关系,方法1是运用两点间的距离公式,思路简单直接,但计算量大;方法2是把图形放在极坐标系下,运用极坐标系中方程的特点,减小了计算量,但对极坐标系的知识要求高;方法3是运用直线的参数方程,亦将计算量减小.方法4借助于斜率与倾斜角的关系,大大减小了运算,体现了解析几何中数形结合的思想.方法5从图形的几何性质出发,运用相似三角形的性质,属于纯几何证法,让我们看到了问题的本质.

3 拓展推广

3.1 在椭圆中的一般化推广

从上面证法5可知,对于一般的椭圆,只要M点为椭圆的右准线与x轴的交点,那么上述性质一定成立,即:

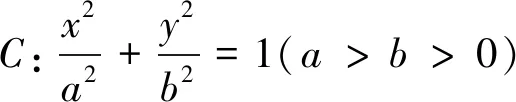
在上述定理中,我们发现焦点F与定点M的横坐标之间存在一定的联系,即乘积等于定值a2,那么,若将F点换成一般的点P(m,0),保证P、M两点的横坐标的乘积为定值a2,是否又有类似的性质呢？笔者借助GeoGebra软件进行探究,得出如下结论:

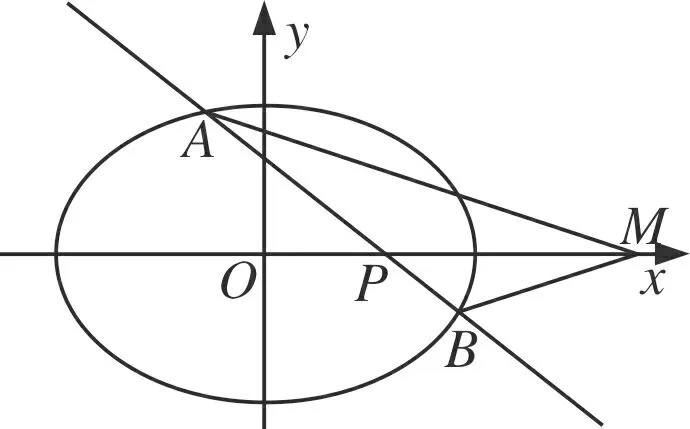
图3

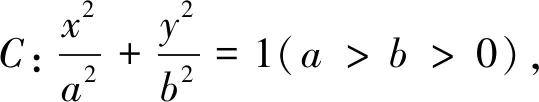
证明当设直线AB与x轴重合时,显然成立;当设直线AB与x轴不重合时,设直线AB的方程为x=ty+m,A(x1,y1)、B(x2,y2),将x=ty+m代入椭圆C的方程，得(t2b2+a2)y2+2tmb2y+(m2-a2)b2=0,则

=0,

从而得直线AM与直线BM的倾斜角互补,所以∠AMP=∠BMP.

图4

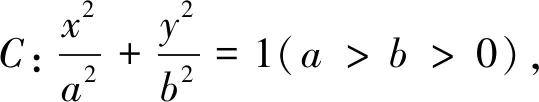
在定理3中,将直线l绕着P点旋转,当A、B两点无限靠近时,∠AMP与∠BMP的大小无限接近,当A、B重合时, ∠AMP=∠BMP=900,此时AM⊥x轴,直线l与椭圆C只有一个交点,直线l与椭圆C相切,于是我们进一步得出结论:

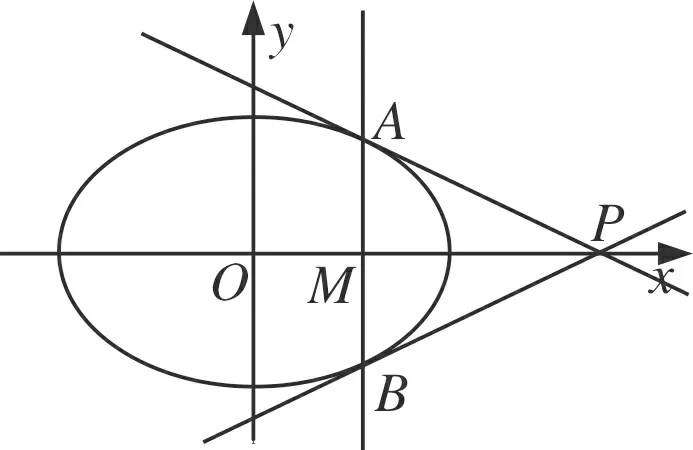
图5

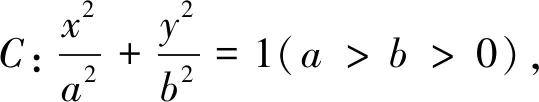
3.2 在双曲线、抛物线中的推广

类比椭圆,在双曲线、抛物线中是否有类似的结论呢？笔者又借助于GeoGebra软件进行了探究,得出以下结论:

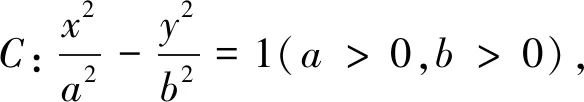
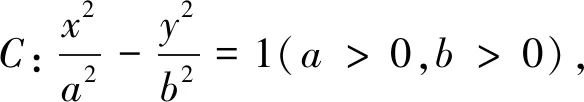
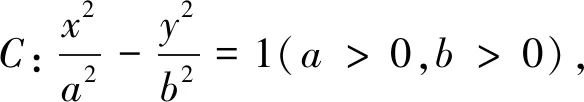
定理6已知抛物线C:y2=2px,点P(m,0)(m>0)是抛物线C内一点,过点P作直线l与抛物线C交于A、B两点,M(-m,0),则∠AMP=∠BMP.

定理7已知抛物线C:y2=2px,点P(m,0)(m<0)是抛物线C外一点,过点P作直线l与抛物线C交于A、B两点,M(-m,0),则∠AMP=1800-∠BMP.

推论3已知抛物线C:y2=2px,点P(m,0)(m<0)是抛物线C外一点,过点M(-m,0)与x轴垂直的直线l与抛物线C于A、B两点,则直线PA、PB与抛物线C相切.

4 背景探源

在以上关于椭圆、双曲线的结论中,都有M、P两点的横坐标之积为定值a2;而在抛物线中,都有M、P两点的横坐标互为相反数,这是偶然还是必然呢？经过研究发现,这与圆锥曲线的极点、极线的知识有关.实际上,在近年来全国各地的高考卷中,有着极点与极线知识背景的试题经常出现,我们虽不能直接利用极点与极线的相关结论进行解答,但教师如果掌握了其中的相关理论,就能从更高的角度看问题,把问题看得更透彻,这对我们教学是有很大帮助的.

借用文[1]给出圆锥曲线中极点与极线的定义:

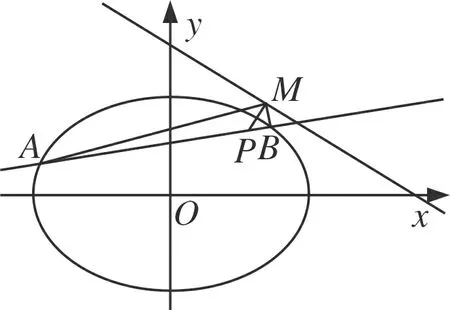
图6

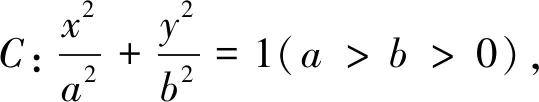
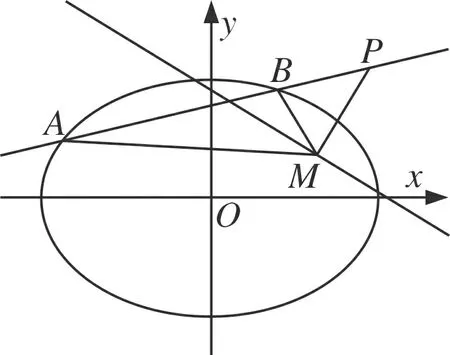
图7

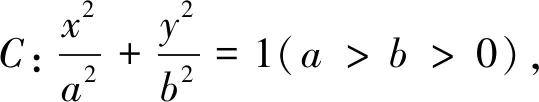
对于以上两个结论,可利用GeoGebra软件验证成立,限于篇幅,在此不再证明,感兴趣的读者可自行证明.

5 高考链接

理解以上结论,对解答一些高考试题有一定的帮助,下面列举数例加以说明.

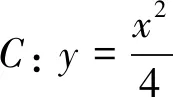
(2)(2015年福建文科数学第19题)已知点F为抛物线E;y2=2px(p>0)的焦点,点A(2,m)在抛物线E上,且|AF|=3,(Ⅰ)求抛物线E的方程;(Ⅱ)已知点G(-1,0),延长AF交抛物线E于点B,证明：以点F为圆心且与直线GA相切的圆,必与直线GB相切.

(3)(2013年陕西卷理科数学第20题)已知动圆过定点A(4,0), 且在y轴上截得的弦MN的长为8. (Ⅰ)求动圆圆心的轨迹C的方程; (Ⅱ)已知点B(-1,0), 设不垂直于x轴的直线l与轨迹C交于不同的两点P、Q, 若x轴是∠PBQ的角平分线, 证明直线l过定点.

以上几例问题的第二问及2018年全国卷解析几何题虽然考查的载体和设问方式各异,但本质上都是在考过定点的动直线与圆锥曲线所形成的等角问题.2018年全国卷考的是已知定点与动直线证明等角.2015年全国卷考的是已知等角探究定点的存在性.2015年福建卷是综合抛物线与圆间接性考等角的证明.2013年陕西卷考的是已知等角证明动直线过定点.无论如何变化,其考查的本质不变,解答的方法也几乎一样.因此,在高三复习备考中我们要重视高考真题的训练,在课堂上要精选典型真题进行讲解,帮助学生把握其实质,掌握其规律,让学生在训练的过程中发散思维、提高能力.

通过本文的探究,我们进一步认识到各圆锥曲线之间规律的统一性,当我们在一个曲线中得到一个规律时,往往可以将之进行推广,得出更普遍、更一般的规律.正如波利亚所说的“解题就像采蘑菇一样,当我们发现一个蘑菇时,它的周围可能有一个蘑菇圈. ”