☉浙江省玉环市清港初级中学 朱雪平

在教学中，往往我们更关注成绩而忽视了错误背后的原因，从学生的错误反思自身教学问题的就更少，评价的反思价值被忽视.那么，教师如何从学生的学情出发，反思自身教学过程缺失，打造“深度”数学课堂？下面本人就以一道让不少学生困惑不解、错误率极高的试题为例，谈谈由它引发的一些思考.

一、分析学生解题思路

题目：已知直线与x轴、y轴分别交于B、A两点，圆C的半径为1，点C的坐标为（0，1）.若点M、N、P分别在圆C、直线l和x轴上，则PM+PN的最小值为（ ）.

图1

本题为九年级上学期期末考试选择题压轴题，从考后统计的数据看，解题错误率偏高.经分析发现，学生的解答存在以下几种类型.

1.无从入手型

动点问题是学生学习的难点，尤其是本题中有M、N、P三个动点，大部分学生遇到问题束手无策，不知道从哪个角度切入.

2.特殊化法型

不少学生尝试在运动过程中找到特殊点，发现当M、P同时运动到O点时，最小值ON等于于是错误地把特殊情况下的最小值当成了本题的答案.

3.思路中断型

部分学生固定M、N，作N的对称点N′，借助轴对称模型转化为求MN′的最小值，但在求最小值时无法转化为过圆心最短和垂线段最短的问题.

4.正确解答型

少数学生认为N′的运动轨迹为直线l关于x轴对称的直线m，当MN′过圆心C时最短，再作点C到直线m的垂线段即有最小值，然后通过相似三角形可得结果为

二、反思教师教学过程

通过分析学生的答题情况，回过头来深入分析题目特点，发现本题涉及的知识点较多，在轴对称问题中加入了动点及过圆心最短、垂线段最短等问题，其中学生对轴对称模型能否综合应用是本题考查的关键.为进一步找到错误的本质原因，选取了其中两个情境进行分析.

情境1：八上课题学习“最短路径问题”

问题1：如图2，某天然气公司分别要向两个新建住宅A、B小区提供天然气，需要在主天然气管道l上修建一个供气站，问：供气站修在主管道的什么地方，可使所用的输气管线最短？

问题2：如图3，供气站修在主管道l的什么地方，可使所用的输气管线最短？

图2

图3

师：你能解决问题1吗？

生：连接AB，与直线l交于点P，点P就是供气站的位置.

师：理由是什么？

生：两点之间，线段最短.

师：很不错，再来看问题2.

学生表示困惑，无人回答.

师：有没有发现问题2与问题1的区别在于A、B位于直线同一侧？只要转化为异侧问题即可解决.

学生表示肯定.

教师板书解答过程，并给出其他类似问题加以巩固.

学生听讲并模仿应用.

情境2：八下“平行四边形”章节复习课

图4

图5

例如图4，菱形ABCD的边长为1，∠ABC=120°，E、F、P分别是AB、BC、AC上的动点，PE+PF的最小值等于________ .

教师出示例题，学生思考后无法解决，教师出示如下解答过程.先找出图中点E关于AC的对称点E′，过点E′作E′F⊥BC于F，交AC于P，利用垂线段最短可知E′F为PE+PF的最小值.再过点B作BG⊥AD于G，根据平行线间的距离相等得出最小值E

以上是我在“应用轴对称求最短路径”教学中的一些片段，细细打磨发现，以上教学过程中存在不少缺失.一是缺少深刻的过程体验.如情境1中我只关注了知识的讲解而忽视了学生学的过程，缺少深刻的过程体验，学生无法内化知识，更不用说推广迁移了，遇到新的问题时无从入手.二是缺少数学本质的揭露.如情境2中我的讲解没有让学生深刻体会以静制动的方法.缺少了数学本质的揭露，导致无法灵活运用知识解决问题.三是缺少知识的系统整合.如情境1中学生获得的知识是零散的、孤立的，缺乏与其他知识的横纵联系，缺少了知识的系统整合，这也是思路中断型学生的成因.

三、打造“深度”数学课堂

为弥补以上教学过程的缺失，让学生经历数学探究的过程，深刻理解数学问题的本质，并学会推广应用，我特从以下几方面着手，改进教学设计，致力于打造“深度”数学课堂.

1.深度设疑，经历数学探究的过程

情境1中，学生解决问题2感到困惑时，教师提问：“你能利用两个问题的区别解决问题2吗？”再“放慢”课堂的脚步，给予学生充足的思考时间和表达空间，使学生经历观察、实验、推理、验证等探究过程，体会遇到新问题要转化为已知的问题，建立两者间的联系.让学生感受丰富的生命体验：主动探索时的困惑，寻找方案时的尝试，解决问题后的快乐.在学生完成问题2后追问：“解决问题时你用的是什么方法？能描述下你的解题思路吗？”学生经历了反思的过程，总结解题的方法和思路，抽象出轴对称模型，才能自主将数学知识上升到思想方法的层次，这也是学习深化的过程.

2.变式训练，触摸数学问题的本质

在情境2的教学中，补充以下两个例题作为原例题的铺垫与拓展.

例1如图6，点P是边长为1的菱形ABCD的对角线AC上一个动点，点M、N分别为AB、BC边的中点，则MP+NP的最小值是__________.

图6

本题是轴对称模型在菱形背景下的简单应用，放在例题前让学生回顾相关知识，为例题的解决做好知识和方法的铺垫.之后，让学生自己尝试解决例题，找到问题的区别在于定点M、N变为动点E、F，通过以静制动，固定E或F点，类比例1的方法就能解决.学生在解题中找到了问题的本质，才能举一反三完成例2.

例2如图7，菱形OABC中，点A在x轴上，顶点C的坐标为（1，3），动点D、E分别在射线OC、OB上，则CE+DE+DB的最小值为_________.

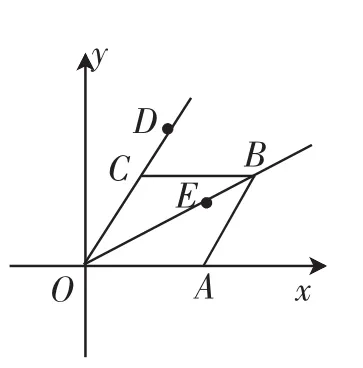
图7

例2是对以上两个例题的拓展与提升.本题涉及了两个动点，需要学生在充分理解轴对称本质的基础上解题.利用第一次轴对称求出CE+DE的最小值为AD，再利用第二次轴对称求出AD+BD的最小值.本题有助于培养学生思维的深度与广度，在学生的自我质疑、自我探究中循序渐进，达到对知识和方法的内化和梳理.

3.综合应用，构建数学知识体系

为了深化轴对称模型，加强知识点的横纵联系，我选择了以下例题，旨在让学生站在全局的观点看问题，在解决综合型问题的过程中构建数学知识体系.

例3如图8，已知点A（-4，8）和点B（2，n）在抛物线y=ax2上.

（1）求a的值及点B关于x轴的对称点P的坐标，并在x轴上找一点Q，使得AQ+QB最短，求出点Q的坐标.

（2）平移抛物线y=ax2，记平移后点A的对应点为A′，点B的对应点为B′，点C（-2，0）和点D（-4，0）是x轴上的两个定点.

图8

①当抛物线向左平移到某个位置时，A′C+CB′最短，求此时抛物线的函数解析式.

②当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由.

本题是在二次函数的背景下对轴对称模型的迁移与应用，将轴对称问题与一次函数、二次函数、平移变换等问题相结合，让学生经历思考探究解决问题的过程，将各部分零散的知识进行系统整合，构建完整的知识体系，这样一来，学生对知识的理解深刻且不易遗忘.第（2）题第②问中求四边形周长的最小值即求A′D+CB′的最小值，通过平移C点至D点，B′点至B″点，可找到问题的本质为轴对称模型，让学生学会从知识系统中提取知识和方法，遇到新的问题能转化为已知的问题，这也是数学教学的最终目标.

有“深度”的数学课堂，既有数学经验积累和数学思想方法感悟的过程，也有知识系统构建的过程.在教学中，我们要善于利用学生的错误资源反思自身的教学，找到错误的本源，立足学情，探寻改进教学的方法，在不断完善中，让我们的数学课堂更有味道、更有实效、更有深度.F