分圆跳频序列的时频二维汉明相关性
2019-03-21许成谦
许成谦,李 鑫
(1. 燕山大学 信息科学与工程学院,河北 秦皇岛 066004;2.燕山大学 河北省信息传输与信号处理重点实验室, 河北 秦皇岛 066004)
0 引言
随着跳频通信技术的高速发展,用户对网络性能要求提高,用户数快速增长,硬件成本降低,提高跳频通信抗干扰性越来越重要。跳频序列的汉明相关函数值是跳频通信抗干扰性标准之一。跳频序列的汉明相关函数值越小,跳频通信抗干扰性越好。
目前跳频序列汉明相关性由只包含时延变量的一维汉明相关函数表示。对跳频序列时延一维汉明相关性的研究取得了显著的成果[1-4]。然而,跳频信号在传输过程中不仅有传输的时延还可能有频率的偏移。文献[5]基于矩阵转换构造了低碰撞区(No Hit Zone,NHZ)跳频序列集。文献[6]首先将跳频序列无碰撞区概念从时延一维扩展到同时考虑跳频序列的时延和频移,给出了时频二维无碰撞区的定义,分析推导了时频二维无碰撞区的跳频序列理论界,并且给出了基于矩阵变换、映射和“等间隔去频隙”构造NHZ跳频序列集的方法,并且这些方法构造的NHZ跳频序列集的序列长度都是ZNt+1(ZNt是一维时延无碰撞区长度)的整数倍。随后针对时频二维相关跳频序列(集)的研究得到了许多结果。文献[7]给出了跳频序列由时频低碰撞区边长值、时频二维移位汉明相关值、频隙个数、序列的长度、序列的个数构成的理论界。文献[8]给出了两种分别基于Welch Costas阵列和Golomb Costas阵列构造时频二维低碰撞区跳频序列集的方法,并指出所构造的序列集在理论界意义下的最优性。文献[9]研究了跳频序列集时频最大周期汉明相关值的理论界,分析了Cai跳频序列集和多项式同余法构造的跳频序列集的时频二维周期汉明相关性。
本文给出了跳频序列长度为奇素数,可供跳频的载频集分别为Ze和Ze∪{∞}上的分圆跳频序列的时频二维汉明自相关性的计算公式,根据计算公式可以得出分圆跳频序列的时频二维汉明自相关性与每个分圆集大小和分圆类个数有关,进而得到频隙集为Ze∪{∞}的分圆跳频序列(集)具有最优时频二维汉明相关性的结论。
1 相关符号和概念
在本文中设a∈Ze,C⊆Ze其中e为正整数,Ze{0,1,2,…,e-1}为模e的剩余类环,定义:
C+a={c+a;c∈C},
aC={ac;c∈C}。
用于控制载波频率跳变的地址码序列称为跳频序列。跳频序列是频率集合F={f0,f1,…,fq-1}上周期为p的序列,表示为x=(x0,x1,…,xp-1),xi∈F,i=0,1,…,p-1。由跳频序列组成的集合称为跳频序列集[10]。
1.1 跳频序列的时频二维汉明相关函数
定义1[7]设频率集F={f0,f1,…,fq-1}是一个加法群,x=(x0,x1,…,xp-1)和y=(y0,y1,…,yp-1)为长度为p的两个跳频序列,若
其中,0≤τ≤p-1,ω∈F,
i+τ≡(i+τ)modp,i=0,1,…p-1,则称Hxy(τ,ω)为x和y的时频二维周期汉明互相关函数。当x=y时,称Hxx(τ,ω)为x的时频二维周期汉明自相关函数。
本文中用


设S是包含M个序列的跳频序列集,其时频二维汉明自相关最大值Ha(S),时频二维汉明互相关最大值Hc(S)和时频二维汉明最大值Hm(S)分别定义为

在以下讨论中,为简化起见,令HaS=Ha(S),HcS=Hc(S),Hm=max{Ha(S)},Hc(S)}。
1.2 跳频序列的时频二维周期汉明相关值的理论界
文献[7]中给出了时频低碰撞区跳频序列理论界。
定理1[7]设频隙集合F={f0,f1,…,fq-1}为q阶加法群。S是F上M个长度为L的跳频序列组成的集合,[0,LHt]×[0,LHf]是S的时频低碰撞区,Ha(S)和Hc(S)分别是最大周期汉明自相关值和互相关值,对于任意正整数Z1,Z2,0≤Z1≤LHt,0≤Z2≤LHf,有
qZ1HaS+qZ1Z2HaS+q(M-1)(Z1+1)(Z2+1)HcS≥
(Z1+1)(Z2+1)ML-Lq。
(1)
在定理1中取Z1=LHf=L-1,Z2=LHf=q-1,就可以得到跳频序列集S的周期时频二维汉明相关理论界。
引理1[9]设F={f0,f1,…,fq-1}为频隙集合,F为Q阶加法群。S是F上M个长度为L的跳频序列组成的集合,那么跳频序列集S的时频二维汉明自相关最大值Ha(S),时频二维汉明互相关最大值Hc(S)和时频二维汉明最大值Hm(S)满足
(L-1)qHa(S)+Lq(M-1)Hc(S)≥(ML-1)L,
(2)

(3)
推论1 设频隙集合F={f0,f1,…,fq-1}是q阶加法群。在频率集F上的跳频序列x=(x0,x1,…,xL-1),那么跳频序列x的时频二维汉明自相关最大值为

(4)
跳频序列x的时频二维汉明相关最大值为

(5)
证明:由引理1可知当跳频序列集S只包含一个序列即M=1时,带入不等式(2)即可得到不等式(4),同理也可得到不等式(5),证毕。
定义2 使得不等式(2)或(3)成立的跳频序列集称为时频二维相关最优跳频序列集,使得不等式(4)或(5)成立的跳频序列称为时频二维相关最优跳频序列,当Ha(x)≥[L/q]+1时,跳频序列称为时频二维相关次最优跳频序列。
2 分圆跳频序列的时频二维汉明相关性分析
2.1 分圆和分圆数的性质
设p=ef+1为奇素数。在有限域GF(p)上的分圆类是C0,C1,…,Ce-1,Ci={αi+te|0≤t≤f-1},0≤i≤e-1,其中α是GF(p)上的一个本原元。e阶分圆数定义为(i,j)=|(Ci+1)∩Cj|,(上角标均为模运算)。
引理2[11]对于任意ω∈Ze 引理3[12] 1)对于任一整数m和n, (i+me,j+ne)=(i,j); 2)(i+j)=(e-i,j-i); 定理2 设p=ef+1为奇素数,并且C0,C1,…Ce-1是有限域GF(p)上分圆类,α是GF(p)上的一个本原元。设F=Ze是频率集,构造一个长度为p的跳频序列x=(x0,x1,…,xp-1)如下: C0={k|xk=0,0≤k Ci={t|xt=i,0≤t≤p-1},1≤i≤e-1, 则序列x形成一个参数为(p,e,Ha)的跳频序列,其中 式中,n1,n2为正整数。当e和f满足如下关系:e=2n1+1,f=2n2,或者e=2n1,f=2n2+1 ,α>2时,跳频序列x为次最优跳频序列。 证明:由文献[4]可知分圆法中e阶分圆类Ci(0≤i≤e-1)的每一个元素表示跳频序列x的频率i在序列x中位置数即时间间隔,那么跳频序列x的时间的延迟等价于分圆类C1中每一个元素的延迟,跳频序列x的频率偏移即码元占用的频段的改变等价于分圆类Ci的i的改变,又由定义1可知h[x(i),x(i+τ)ω]=|(Ci+ω+τ)∩Ci|,则在该构造下跳频序列x的二维汉明相关性计算公式如下: max|{-τ}∩Cω|+|{τ}∩C-ω|, 其中,0<τ 由引理2的2)知 所以,Ha(x)的值主要由max{|{-τ}∩Cω|+|{τ}∩C-ω|}决定,由分圆时间和频率的周期性和模运算可知-τ=p-τ,C-ω=Ce-ω,则有 max{|{-τ}∩Cω|+|{τ}∩C-ω|}= max{|{p-τ}∩Cω|+|{τ}∩Ce-ω|}, 而|{τ}∩Ce-ω|=1必成立,|{p-τ}∩Cω|的值等价于方程 p-τ=αω+kemodp,0≤k 解数,因此有 当e=2n1,f=2n2,n1,n2为正整数时, |{p-τ}∩Cω|=1; 当e=2n1,f=2n2+1,α=2,n1,n2为正整数时, |{p-τ}∩Cω|=1; 当e=2n1,f=2n2+1,α>2,n1,n2为正整数时, |{p-τ}∩Cω|=0; 当e=2n1+1,f=2n2,n1,n2为正整数时, |{p-τ}∩Cω|=0。 综上所述 式中,n1,n2为正整数。 当e为奇数,f为偶数,或者e为偶数,f为奇数,α>2时,将分圆跳频序列的频率集大小q=e,序列长度L=p,代入到推论1的式(4)中,且由定义3可知Ha(x)=f+1,跳频序列x为次最优跳频序列,证毕。 定理3 设p=ef+1为奇素数,C0,C1,…,Ce-1是有限域GF(p)上分圆类,α是GF(p)上的一个本原元。设频率集是F=Ze∪{∞},构造一个长度为p的跳频序列x=(x0,x1,…,xp-1)如下: x0=∞, 则序列x形成一个参数为(p,e+1,f)的跳频序列,且该序列为时频二维相关最优跳频序列。 证明:由定理2的证明可知当ω=∞时,等式(1)的右边的最大值为0,因此 又因为频隙集大小为e+1,然而频隙的变化对于频隙∞产生的变化相对于其本身值可以忽略不计,所以此时跳频序列集时频二维汉明相关性所对应的频隙集大小为e,则将L=p,频隙数为e,代入到推论1不等式(4)中Ha=「p/e⎤=f。又由定义3知该序列为时频二维汉明相关最优跳频序列。证毕。 则序列集S={x0,x1,…,xe-1}为(p,e+1,f)跳频序列集,并且该序列集为时频二维相关最优跳频序列集。 证明:定理3已经证明Hxkxk(τ,ω)=f成立。下面计算xk和xl的互相关性Hxkxl(τ,ω)的值,其中0≤τ≤p-1,ω∈(0,e-1],k≠l。 当τ≠0,ω=0时, 当τ=0,ω≠0时, 其中1表示两个序列只有一个频率为∞时产生了碰撞,其余都没有产生碰撞; 当τ=0,ω=0时, 当τ≠0,ω≠0时, 设τ∈Ch,由引理3的2)得 由引理3的4)得 f-1+1=f。 综上可得Hxkxl(τ,ω)=f,即Hc(S)=f。 将L=p,q=e,代入到引理1的式(3)中满足Hm(S)=「L/e⎤=f,由定义3得该跳频序列为时频二维汉明相关最优跳频序列集,证毕。 例1 设p=13=2×6+1其中e=6,f=2,并且α=2是有限域GF(13)上的本原元,分圆类如下: C0={1,12},C1={2,11},C2={4,9} C3={5,8},C4={3,10},C5={6,7}, 根据定理2,可以构造一个(13,6,4)跳频序列 x=(0,0,1,4,2,3,5,5,3,2,4,1,0), 根据定理3,有(13,7,2)时频二维汉明相关最优跳频序列, y=(∞,0,1,4,2,3,5,5,3,2,4,1,0), 满足最优性条件。 例2 设p=23=2×11+1,其中e=11,f=2,α=5是有限域GF(23)上的本原元,分圆类如下: C0={1,22},C1={5,18},C2={2,21} C3={10,13},C4={4,19},C5={3,20}, C6={8,15},C7={6,17},C8={7,16}, C9={11,12},C10={9,14} 根据定理4,可以构造一个跳频序列y0如下: y0=(∞,0,2,5,4,1,7,8,6,10,3,9,9, Ha(y0)=2=f。 类似地,可以构造一个跳频序列y3如下: y3=(∞,3,5,8,7,4,10,0,9,2,6,1,1, Ha(y3)=2=f,Hc(y0,y3)=2=f。 同理可构造所有的yi,0≤i≤10,计算所有跳频序列yi得Hm(yi)=2=f,则跳频序列集S={y0,y1,…,y10},Hm(S)=2=f,满足最优性,所以跳频序列集S为时频二维汉明相关最优跳频序列集。 本文分别对载频集为Ze和Ze∪{∞}的分圆跳频序列(集)的时频二维汉明相关函数进行了计算,由计算结果知在载频集为Ze∪{∞}上分圆跳频序列(集)当跳频序列长度为奇素数时具有时频二维汉明相关最优性。

2.2 频率集上的分圆跳频序列的时频二维汉明相关性分析
2.3 频率集F=Ze∪{∞}上的分圆跳频序列的时频二维汉明相关性分析
Ci={t|xt=i,0≤t≤p-1},0≤i≤e-1,
3 频率集F=Ze∪{∞}上的分圆跳频序列集的时频二维汉明相关性分析
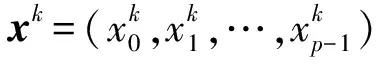










4 实例
Ha(x)=f+2=4。
Ha(y)=2=f。
3,10,6,8,7,1,4,5,2,0),
6,2,9,0,10,4,7,8,5,3),5 结论
