论向量在解决高中数学问题中的应用
2019-03-07江苏省宿迁中学
■江苏省宿迁中学 蒋 健
高中数学试题复杂多变,应用向量的几何、坐标运算以及相关性质,对数学试题进行转化,可大大降低解题难度,使学生迅速找到解题突破口,提高解题正确性,帮助其树立良好的解题自信,因此,授课中应做好数学试题汇总,向学生展示向量在解题中的应用,提高学生向量应用意识,使其牢固掌握、灵活应用这一重要的解题工具。
一、向量用于解答最值试题
求解最值是高中数学最为常见的一种题型,解题方法多种多样,可应用均值不等式、函数、向量法求解,其中向量可化抽象为具体,不仅有助于理解题意,而且还能简化解题步骤,及时解出正确结果。
授课中为使学生认识到向量法在解答最值问题中的妙用,掌握向量解题的技巧,应优选经典例题,为其详细板书解题过程,给其解答类似习题,提供良好指引。
例1,已知a,b,c∈R,a+2b+3c=6,则a2+4b2+9c2的最小值为______。
很多学生看到该题目采用不等式知识求解,但多数无功而返,部分学生虽然得出正确结果,但花费时间较多,代价太大,在测试中是不可取的。授课中,可引导学生认真观察已知条件以及要解决的问题,联想所学的向量知识,应用向量方法解答。
解题中可设m=(1,1,1),n=(a,2b,3c),根据向量 性 质m · n≤|m| · |n|,可 得
该题从向量角度入手,巧妙运用向量性质进行转化,经过简单计算便得出正确结果,解法新颖,使学生眼前一亮,使其掌握解答最值问题的又一重要思路,很好地锻炼其解题思维,获得预期教学效果。
二、向量用于解答三角形试题
解三角形是高考常考题型,占有较高分值,通常应用正弦、余弦定理进行求解。但部分试题应用向量知识,可获得事半功倍的良好效果,因此,授课中应注重讲解三角形相关知识的向量表示,引导学生构建三角形与向量之间的关系。另外,创设相关问题情境,鼓励学生运用向量法解答,并做好向量法解题的总结与反思,提高三角形试题解题效率。
例2,在△ABC中,角A、B、C对应的边分别为a、b、c,若则△ABC 最小角的正弦值为:____。
观察可知,因题干中给出有关向量的已知条件,因此,学生不难想到应用向量法解答。解答该题目的关键在于灵活转化给出的等式关系,确定三角形的最小角,而后运用余弦定理进行求解,具体解题过程如下:

在解答该题目中,部分学生盲目求解,未搞清楚最小角便急于计算,结果走不少弯路。通过该题目的解答,可使学生深刻地认识到向量的工具性以及在解答三角形试题中的重要性,很好地提高其应用向量解答三角形试题的意识,为其顺利、高效解题奠定良好基础。
三、向量用于解答立体几何试题
立体几何涉及的知识较多,对学生的空间想象能力要求较高。解答立体几何试题有常规方法和向量方法,其中向量方法只要找到相关点的空间坐标,借助空间向量知识求解即可,对空间想象能力不好的学生而言是一种重要解题方法。授课中为使学生牢固这一方法,应注重相关例题的讲解,提高学生空间向量的应用方法与技巧,灵活用于解答各类立体几何试题。
例3,如图1,四棱锥P-ABCD 中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,点M 在PC 上,试确定点M的位置,使得BP⊥面ADM。
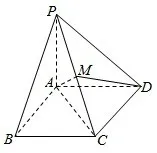
图1
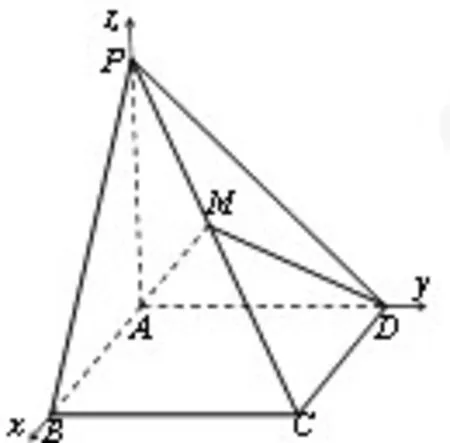
图2
分析可知,该题目中存在三条边垂直的情况,因此,可考虑采用向量法求解。以A点为原点,以AB、AD、AP 三条边为x、y、z 轴,建立空间直角坐标系,如图2所示。则P(0,0,1),A(0,0,0),B(2,0,0),C(2,1,0),D(0,1,0),设M(a,b,c),∵M 在PC 上,则令1),即,(a,b,c-1)=λ(2,1,-1),则M(2λ,λ,1-λ),要想满足BP⊥面ADM,则,则,可知M在靠近点P,CP线段的五等分点上。
在立体几何试题中确定点的坐标难度较大,采用常规做法多数学生不知如何下手,而使用向量,将其转化为坐标的形式,问题便迎刃而解。
四、向量用于解答解析几何试题
高中数学中解析几何试题以计算烦琐、难度大而著称,是各类测试的重要失分题型,因此,授课中为提高解析几何试题的正确性,除为学生讲解常规解题方法,还应引导学生具备灵活应用所学的意识,即用好向量这一重要解题工具。以经典题型为例,与学生一起分析,采用向量知识寻找解题突破口,使学生认识到向量在解答解析几何试题中的便捷性。
例4,如图3,椭圆的中点在坐标原点,焦点在x轴上,A1、A2、B1、B2为椭圆的顶点,F2为右焦点,延长B1F2和A2B2交于点P,若∠B1PB2为钝角,则该椭圆的离心率的取值范围为:______。
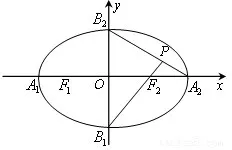
图3
解答该题的关键在于怎样正确运用“∠B1PB2为钝角”这一条件。根据所学知识不难想到运用向量知识可表示出钝角这一条件,即,借助对应的坐标关系便可求解。
由已知条件可知A2(a,0),B2(0,b),F2(c,0),B1
解答解析几何试题时,能够读懂,正确利用已知条件是关键。通常将已知条件转化为向量之间的关系,实现求解。正如本题,使用向量之间的关系表示钝角,很快找到解题突破口。
五、结语
向量与高中数学其他知识点联系紧密,在解题中应用广泛,可显著提高解题质量与效率,因此,授课中应做好高中数学试题总结,明确能应用向量解题的题型,尤其针对不同题型优选经典习题,讲解向量在解题中的具体应用,鼓励学生认真体会,反思解题过程,掌握向量解题的技巧,不断提高解题水平与解题能力。
