魏高荣

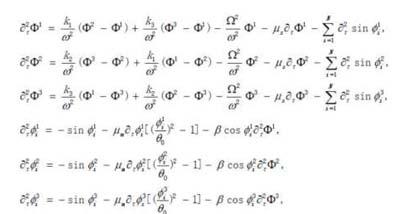
【摘 要】研究多群体机械振子系统中的奇异态和等分相位的相同步。本文通过调节群体间节拍器自然频率和耦合强度来研究多群体的集体动力学特性。在多群体环状网络中，当群体个数为3时，随着耦合强度的增加，系统会逐渐出现等分相位的相同步，奇异态和完全同步;而当群体个数超过3时，奇数群体系统会随着耦合强度的增大，逐渐出现等分相位的相同步，奇异态，等分相位的相同步，奇异态，完全同步;偶数群体随着耦合强度的增加，系统逐渐出现反向相位的相同步，奇异态，等分相位的相同步，奇异态，完全同步。在多群体链状网络中，当群体个数为3时，随着耦合强度的增加，系统会逐渐出现反向同步，奇异态，完全同步;而当群体个数超过3时，系统的相图会变得相当复杂。通过观察序参量在复平面上的分布图、序参量的随时演化图以及归一化的角频率图，我们将对不同动力学进行分析，并给出了不同节拍器频率下，调节耦合强度时两种网络拓扑中系统不同动力学区域的相图。

【关键词】奇异态;机械振子;相位同步

中图分类号： O437 文献标识码： A 文章编号： 2095-2457（2019）36-0116-003

DOI：10.19694/j.cnki.issn2095-2457.2019.36.053

0 引言

近年来，关于Kuramoto相位振子模型的研究[1]揭示了“奇异态”的可能性，在同一时刻，系统中的一部分振子处于同步状态而另一部分振子处于去同步状态，这种集体的行为被Abrams[2]称为奇异态。奇异态最初是在非局部耦合振荡器中发现的，后来在全局耦合振荡器实验中也发现了奇异态。之后1980年Winfree[3]研究了振蕩同步问题，这是奇异态问题关键性工作。自此，大量同步现象被发现。关于复杂系统同步理论的研究，以及对各种随机干扰源和不同网络拓扑的同步分析和研究，为奇异态奠定了大量的理论基础。

奇异态在光学实验，生物实验以及机械实验中得到了验证。在2013年，Martens和他的实验团队设计了一个实验，通过两个群体的机械振子耦合来实现奇异态[4]，他们发现当系统的耦合强度较小时，系统会呈现反向同步，当耦合强度逐渐增大时，会出现奇异态。Hagerstrom通过液晶光调制器实验发现了光学耦合映射晶格中的奇异态。2016年，Blaha[5]和他的研究团队在Martens工作基础上，设计了三群体链状的机械振子系统，来研究奇异态。Omli等人在机械摆实验中发现了处于混沌状态的奇异态行为。研究发现当每个群体中的节拍器只有三个时，不会产生奇异态。此外，当群体间的耦合不对称时，系统会很容易出现奇异态。H.Ulrichs等人在实验中对节拍器的同步与混沌也有一些新的发现，推动了复杂系统关于同步理论的研究。

本文主要研究环状多群体和链状机械振子拓扑网络中的奇异态和等分相位的相同步。考虑到振荡器自然频率和耦合系数不同，我们将固定群体间的振荡器自然频率，通过调整耦合系数和节拍器的参数与本征频率来观察奇异态和等分相位的相同步。本文首先给出系统的模型和初始条件，然后通过调整参数和群体数量来分析我们的数值模拟结果，最后总结从我们的数值模拟中发现的相关现象。

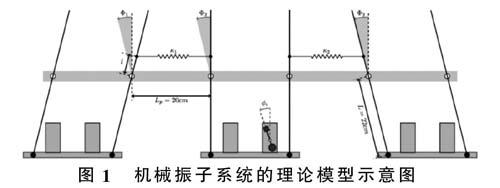
图1 机械振子系统的理论模型示意图

1 模型

我们在先前的一些机械振子拓扑网络[5]的奇异态研究基础之上，将两群体网络结构扩展到三群体网络结构中，并在此基础之上进行了多群体网络结构的研究。图1是三群体机械振子理论模型示意图，模型有三个托盘，每个托盘可容纳15个节拍器。k1、k2、k3表示群体间的耦合强度，Φ1、Φ2和Φ3表示群体1、2和3的偏角。

其动力学方程由以下的方程进行控制：

■

其中i表示每个种群中节拍器的数量。k1、k2和k3是耦合系数。■表示每个群体中节拍器的偏角。二阶导代表惯量项，ω表示节拍器的特征频率。μs和μm表示节拍器和托盘的耗散，θ0初始偏角，■特征频率有关的参数。

2 数值模拟

前期我们做了很多组数值模拟进行数据观察，分别做了3群体，4群体，5群体，6群体，7群体，8群体9群体网络拓扑数值模拟实验。为了方便成果的展示，在本节中我们将选取3群体和6群体环状结构的机械振子网络拓扑结构，他们的初始条件分别为{DDS，DDDDS，DDDDDS}，其中S表示同步群体，D表示非同步群体，非同步群体中节拍器的初始偏角由随机数发生器生成。每个群体中节拍器的数量都是15。我们使节拍器的初始位移角在区间[-19。，19。]内随机均匀分布，设定了同步群体的初始条件■。托盘和节拍器初始速度设为零，■，我们还设定k1=k2=k3=k。我们固定节拍器的频率f，通过调节耦合系数k来观察各群体机械振子网络的动态演化。

图2

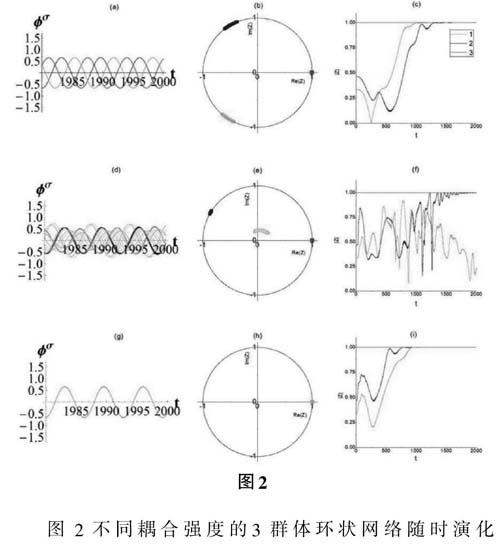
图2不同耦合强度的3群体环状网络随时演化图。最左边的一列是节拍器的随时演化图，中间一列是序参量Z在复平面上的分布图，最右边一列是序参量的模。（a），（b）和（c）k=4，等分相位的相同步;（d），（e）和（f）k=17.5，奇异态;（g），（h）和（i）k=25完全同相同步。三个群体的颜色分别问绿色，蓝色和红色。

首先，我们固定节拍器的自然频率f=208bpm，通过调节耦合强度k来观察系统的变化。在图2（a）中，我们发现三个群体以同样的相位差2π/3分别同步，我们称为等分相位的相同步。为了测量各群体中机械振荡器的相干度，我们引入了序参量Zσ（t）和序参量的模Z，其中σ=1，2，3分别1群体，2群体和3群体，当序参量的模Z=1时，表示群体呈同步状态;当序参量的模Z<1时，表示群体呈相干态。图2（b）是序参量在复平面上的图，Z1，Z2和Z3呈2π/3相位差均匀地落在圆上;在图2（c）中可以观察到，同步群体序参量的模Z3恒等于1（红色），非同步群体序参量的模Z1（绿色），Z2（蓝色）随时间演化从0逐渐增长到1，最终等于1。当耦合强度k增长到17.5时，系统表现为奇异态如图2（d）所示，而图2（e）和图2（f）是k=17.5对应的序参量和序参量的模。群体2和群体3的序参量落在圆上，群体1在群内，相应的序参量的模Z1在不停地震荡，表明群体1是不同步的，而群体2和群体3是同步的。

我们继续增加耦合强度k到25，系统进入完全同步状态，此时三个群体完全同步如图2（g）所示，我们还可以从图2（h）中也可以清楚地观察到系统进入完全同步状态。

图3

图3不同耦合强度的6群体环状网络随时演化图。前5个群体是非同步群体，他们的颜色分别为黑色，蓝色，绿色，橙色和紫色，第6个群体是同步群体，他的颜色是红色，节拍器的频率f=160bpm。（a），（b）和（c）k=2，反相同步;（d），（e）和（f）k=7.5，等分相位的相同步;（g），（e）和（i）k=15.5，奇异态;（j），（k）和（l）k=20，完全同相同步。

首先，我们设定k的值为2。在图3（a）中，我们观察到系统呈现反向同步，其中1，2，3群体和4，5，6群体分别同步。在图3（b）中，我们发现Z1，2，3和Z4，5，6分别落在圆的两侧。其中6群体序参量的模Z6恒等于1，而Z1，2，3，4，5快速地从0增长到1。我们继续将耦合强度k增加到7.5，如图3（d）所示，系统表现为等分相位相同步，系统的序参量以相位差为π/3分布在圆上。

我们继续增加耦合强度k的值到15.5，系统表现为奇异态。如图3（g）所示，红色群体始终保持同步，而其余5个群处于混乱状态。从序参量在复平面的图中，我们发现红色群体坐落在圆边上，黑色和紫色群体完全在圆内，而绿色蓝色和橙色群体在圆边界线周围;我们观察序参量的模图3（i），黑色和紫色群体一直在1以下振荡，而其余群体最终会达到1。最后，继续增加k的值到完全同步状态，此时所有群体都处于同步状态。

图4

图4数值模拟相图，（a）3群体链状网络结构，初始条件是DDS;（b）3群体环状网络结构，初始条件是DDS;（c）6群体链状网络结构，初始条件是DDSDDD;（d）6群体环状网络结构，初始条件是DDDDDS。颜色表示从数值模拟中推断出的相位区域，红色表示完全同步，绿色表示奇异态，橙色表示等分相位的相同步，紫色表示相干态，蓝色表示反向同步。相图的横坐标是耦合强度k，纵坐标表示节拍器的自然频率f。

图4显示了不同节拍器频率下的系统动力学和耦合强度的关系图。左边三幅图是链状网络拓扑结构，右边三幅图是环状网络拓扑结构。如图4（a），（b）所示，在三群体链状网络拓扑结构中，随着耦合强度的增加，链状系统依次表现为反向同步，奇异态，完全同步;而环状依次表现为等分相位等相同步，奇异态，完全同步。随着群体数目的增加，系统的相图会变得复杂一些。如图4（c），（d）所示，在链状6群体拓扑网络结构中，系统依次表现为反向同步，奇异态，反向同步，奇异态，相干态，奇异态，完全同步;在环状6群体拓扑网络结构中，系统依次表现为反向同步，奇异态，等分相位等相同步，奇异态，完全同步。

3 结论

在本文中，我们研究了多群体机械振子环狀拓扑网络结构和链状拓扑网络结构。我们在环状群体数值模拟中发现在奇数群体中，当系统的耦合强度足够小时，系统表现为等分相位相同步，而在偶数群体中，系统则先表现为反向同步，奇异态，然后才是等分相位相同步。对于3群体，系统会随着耦合强度的增加依次表现为等分相位等相同步，奇异态，完全同步。当系统的群体数量大于3时，奇数群体的相图依次表现为等分相位的相同步，奇异态，等分相位等相同步，奇异态，完全同步;偶数群体相图依次表现为反向同步，奇异态，等分相位等相同步，奇异态，完全同步。

我们在对链状群体数值模拟中发现，对于3群体，系统会随着耦合强度的增加依次表现为反向同步，奇异态，完全同步。群体数量超过3时，系统的相图会变得相当复杂，相图区域则大体相同。如图4（c）所示，随着耦合强度的增加，系统依次变现为反向同步，奇异态，反向同步，奇异态，相干态，奇异态，最后进入完全同步。

【参考文献】

[1]D.M.Abrams，R.Mirollo，S.H.Strogatz，et al.Solvable model for chimera states of coupled oscillators.Physical Review Letters[J].2008，101（8）：084103.

[2]D.M.Abrams，S.H.Strogatz.Chimera states for coupled oscillators.Physical Review Letters[J].2004，93（17）：174102.

[3]A.T.Winfree，The geometry of biological time[M].Springer-Verlag.Berlin，Germany，1980.

[4]E.A.Martens，S.Thutupalli，A.Fourriere，et al.Chimera states in mechanical oscillator networks.Proceedings of the National Academy of Sciences[J].2013，110（26）：10563-10567.

[5]K.Blaha，R.J. Burrus，J.L.Orozcomora，et al.Symmetry effects on naturally arising chimera states in mechanical oscillator networks.Chaos[J].2016，26（11）：116307.