基于图正则化和l1/2稀疏约束的非负矩阵分解算法
2018-11-15陈志奎
张 旭,陈志奎,高 静
(大连理工大学 软件学院,辽宁 大连 116620)
1 引 言
随着计算机科学的发展,传统的数据挖掘与机器学习方法得以横跨多个学科,在诸多领域得到重要的应用.例如,医学疾病的诊疗和生物学研究过程中,组织细胞的基因表达谱能够以高维数据的形式导出,这为应用数据挖掘手段对其进行进一步分析和处理提供了可能.然而受限于现有获取方式,所有检测到的基因全部被导出,实际起表达作用的基因可能在其中只占小部分.这导致得到的基因谱数据集往往规模庞大、形式复杂,维度远大于样本实例数;同时包含大量冗余,传统数据挖掘算法难以发挥其性能.
为解决该问题,对原始基因表达谱数据进行维数约简[1]是最行之有效的方法之一.该方法通过对原始数据空间进行数学投影变换以获得新的特征空间.较之原始空间,该空间维度大幅精简,概括能力更强,因而可以更好地描述基因数据.而基因数据通常以矩阵形式进行存储,对大规模数据的处理可直观理解为高维矩阵的分析,这就为使用矩阵分解方法进行维度约简提供了条件.传统含负分解方法由于分解结果中的负元素缺乏直观的物理意义[2],在实际应用中有着很大局限性.另一方面,因为基因样本规模庞大,且样本之间存在相互联系,线性变换的过程中可能会破坏基因谱数据的内部结构.故此,基于非负矩阵分解思想的方法由于实现了原始矩阵维数的非线性约减,且通过非负约束保证了分解后元素的物理意义,甫一提出便得到了广大研究人员的重视.1999年,Lee和Seung在前人研究基础上进行总结归纳,于《Nature》上首次正式提出非负矩阵分解方法(Non-negative matrix factorization,NMF)[2]的概念,并证明了其收敛性,为矩阵分解问题开辟了新的思路.其后的十几年里,非负矩阵分解研究方兴未艾,广大学者纷纷将NMF方法进行推广和改进.时至今日,NMF已被广泛应用到基因及细胞分析领域的研究中[3].并逐渐成为最受欢迎的多维数据处理工具之一.NMF在维数约简上有着得天独厚的优势:通过结合流形学习,能够较为完整地保持数据原有的内部空间结构;添加稀疏约束后,也可以较好地抑制噪声.迄今为止,已有很多学者将稀疏的判别信息与流形思想相结合,对NMF算法进行改进[4,5].
流形学习(Manifold Learning)是近年来流行的机器学习方法.流形思想将高维数据映射至低维空间以揭示数据的本质结构,在维数约简上得到广泛应用[6].Cai等人将该思想引入,提出图正则化非负矩阵分解(Graph Regularized nonnegative matrix factorization,GRNMF)[7],并在之后通过一系列研究对其应用方式进行拓展,进一步提升了非负矩阵分解保存原始数据局部特征的能力[8].
非负约束使得基于非负矩阵分解的方法其结果天然具有一定程度的稀疏性.从数据角度这意味着分解得到的矩阵中将包含很多0元素.NMF在稀疏性的作用下,得以使用更少元素表示原有数据,节省存储空间,为数据表达提供一种高效的策略[9].在实际应用中,这种天然的稀疏性往往不够充分,基于实际需求,研究人员常结合稀疏表示理论,在目标函数中引入稀疏性约束,以合理控制NMF结果的稀疏程度,达到更优的分解效果,使结果更具实际应用意义.稀疏编码思想与NMF相结合的方法由Hoyer在2002年首先提出,该方法利用欧氏距离的平方加上l1范数,得到一种非负稀疏编码(Nonnegative sparse coding,NNSC)算法,并通过实验证明了其分解结果在稀疏程度上的优势[10].随后Hoyer对NNSC算法作了进一步改良,利用非线性投影实现对稀疏性的精确控制,给出一种介于l1范数和l2范数之间的稀疏度计算准则并提供相应软件包,极大地促进了稀疏约束NMF研究和应用的发展[9].
通常使用的l1约束在分解含噪声数据时,稀疏表示的有效性受到干预,结果可能仍含有较多噪声,影响降噪效果[11].徐宗本等人针对l1稀疏性问题提出了更加稀疏的l1/2正则理论,并对求解算法和收敛性进行了分析[11].很多学者也对lq范数约束在q取不同值时对NMF算法稀疏性的影响进行研究,验证了l1/2约束在稀疏性表示上的优势[12].近年来,已有更多算法使用了l1/2约束的思想[13,14].
综上所述,针对基因表达谱数据高维度、高冗余的特点,本文提出了一种基于非负矩阵分解的算法,结合图正则化思想和使用l1/2范数的稀疏约束,进一步加入了去噪处理,对NMF算法进行改进,使之得以更好地应用于肿瘤基因表达谱数据的维度约简工作中.实验表明,相较传统方法,该算法在处理含有大量冗余的肿瘤基因表达谱数据时更加有效.
2 非负矩阵分解理论
NMF的基本思想是任意给定一个高维非负矩阵X,可以找到两个低维的非负矩阵W和H,使得W与H的乘积近似地逼近原始矩阵,从而将原矩阵分解成两个非负矩阵的乘积.其数学模型为:
X≈WH
(1)
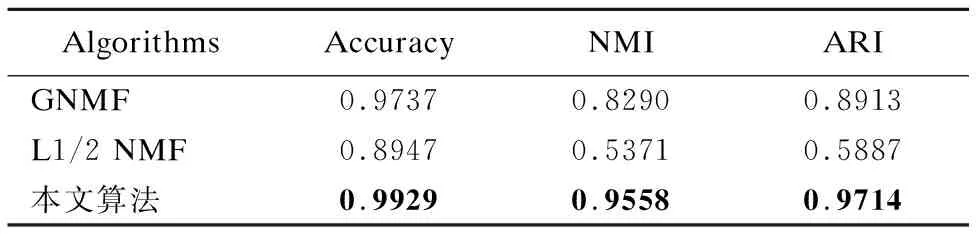
若原始矩阵X是L×P的矩阵,则W为L×N阶矩阵,H为N×P阶矩阵,其中N (2) 在基本的NMF目标函数加上范数约束的方法不仅表示简单,易于理解,而且可以根据具体情况对不同变量附加稀疏性限制,从而得到期望的性质.此外,图正则化方法,噪声处理等方法和演化,都可以通过不同方式被添加到目标函数中.为了将稀疏编码理论与NMF算法相结合,通常对分解后的系数矩阵H进行稀疏约束.稀疏约束的选择一般采用范数约束的方法,常用的包括l1范数和l2范数[9,16],lp范数(0≤p<1)约束在p等于1/2的时候目前被认为是一种行之有效的方法[14]. 使用传统NMF及其衍生算法进行基因表达谱数据集的维度约简工作时,由于原始数据维度较高且含有大量冗余和噪声数据,在没有进行对应处理的情况下,算法性能难以发挥,效果并不够尽如人意.针对基因表达谱数据高维度、高冗余的特点,本文基于非负矩阵分解方法的思想,结合图正则化思想和稀疏性约束,进一步加入去噪处理,对NMF算法进行改进,提出的算法对处理过度冗余的高维基因表达谱数据特别有效.此外,区别于传统稀疏算法中使用的l1范数约束,我们选择l1/2范数进行稀疏性约束,进一步提升了算法的性能. 为了引入噪声项的定义,我们将原始数学模型定义为: X=WH+E (3) 之后为了得到最优解,目标函数定义为: (4) 其中λα是调整稀疏程度的参数;λβ∈R+是一个标量,用于调整流形约束的权重.λγ是控制降噪的参数.Tr(·)是矩阵的迹.L是一个拉普拉斯(Laplacian)矩阵,可以由图权重矩阵G和对角矩阵D由以下公式计算得到: L=D-G (5) 对于给定的两个实例yi和yj,使用高斯核度量计算实例间的相似度,从而得到权重矩阵G: (6) 之后可以计算对角矩阵D: Dii=∑i=1Gij (7) 对目标函数的优化过程等价于如下公式的最小化问题. (8) 可以使用迭代更新的办法解决.基本思路是固定其他变量,对W,H,E分别进行更新.具体的更新优化过程如下: 3.2.1 更新E 首先我们需要证明噪声项的引入不会影响分解过程中非负性的保持,以便采用非负矩阵分解的经典思想对该问题进行优化求解.当固定W,H时,对E的更新优化问题变为: (9) 这是一个带l1范数约束的最小化问题,可以通过软阈值操作符的方式进行求解.其更新规则如下: (10) 通过该更新规则可以保证X-E≥0.证明如下: 综上,在上述更新规则下,可以保证X-E≥0. 通过证明,我们可以保证加入去噪处理后矩阵元素的非负性.由此我们在接下来的工作中,就可以利用一般非负矩阵分解的方法来进行对W,H的迭代更新. 3.2.2 更新W 为了方便说明,因为我们已经证明了X-E≥0,我们令Z=X-E. 当固定H,E时,对W的更新优化问题变为: (11) 由于我们已经知道Z非负,则该优化问题属于一个非负二次规划问题,和传统非负矩阵分解模型类似,可以参考传统非负矩阵分解模型的迭代更新规则[16]进行处理.相应的,我们得到用于迭代更新W的更新规则如下: (12) 3.2.3 更新H 固定W,E时,对H的更新优化问题变为: (13) H可以看作是实例在低维空间中的表示,图正则化思想为了在低维空间保持实例的原始结构,需要用下面的式子对低维表示的平滑性进行度量: (14) 对R进行变换,可得: =Tr(HLHT) (15) 因此在对H进行更新时,需要考虑正则化项Tr(HLHT).参照Cai提出的图正则化优化理论[8],我们使用梯度下降的方法对H进行优化: 设更新H的目标函数为O,有如下的加法更新规则: (16) 其中δi,j是步长参数. 令δi,j=-hi,j/2(WTWH+λβHDT)i,j,可得: (17) 对于l1/2稀疏约束项,我们参照已有的添加稀疏约束的方法[13]. 综上,我们可以得到用于迭代更新H的更新规则如下: (18) 本节结合前文对算法模型和优化过程的介绍,给出本文提出算法过程的简要描述(见表1). 我们使用两个取自真实采样的常用基因数据集,ALL-AML和Colon[17],用于衡量算法的性能.ALL-AML数据集包含38个实例的5000个基因,包括27个ALL细胞和11个AML细胞.Colon数据集中包含62条实例,表示62个组织的2000个基因,其中40个组织是肿瘤,另外22个活检是从同一患者健康的组织部分收集而来. 该理论已经得到证明:当维度约简处理后的维度等于实际类标签数量时,后续聚类中得到的结果无论从开销和性能上都相对优秀[18].因此我们选择聚类领域常用的评价标准,包括正确率(Accuracy,ACC)、标准互信息(Normalized Mutual Information,NMI)和兰德指数(Adjusted Rand Index,ARI[19])进行评估.它们的取值范围都在[0,1]之间.ACC用于描述点和簇的一一对应关系,其原理是使聚类的结果和真实的结果尽可能匹配,ACC越大,代表聚类的效果越好.令qi为数据实例xi使用聚类算法得到的簇标签,pi为数据实例xi的真实簇标签,则ACC定义如下: (19) NMI[20]基于互信息的方法来衡量聚类效果,需要实际类别信息.它代表当一个类的信息已知的时候,对推测出关于另一个类的信息有多少帮助.若两个类没有共同的信息,即互信息为0.值越大意味着聚类结果与真实情况越吻合.令算法得到的聚类结果为C,给定聚类标签为R,H是来自聚类集合的熵信息,可以得到NMI的定义. (20) 表1 算法描述 类似的,ARI的计算方式可以由如下公式定义: (21) 在对比算法的选择方面,由于我们的算法结合了这两类算法的思想,我们选择GNMF[11]和l1/2NMF[8]进行对比.GNMF是图正则化的基本非负矩阵分解方法,通过在分解过程中添加几何分布信息提高算法性能;l1/2NMF对分解后的系数矩阵添加l1/2范数的稀疏约束. 实验中我们随机产生数据集实例的输入顺序,进行多组实验,并在每组内进行多次重复实验.为了公平地对比算法在理想情况下可能表现的最佳性能,对于所有的算法,我们都使用并记录它们的参数为最优值时,所能得到的最好结果.算法需要提供维度约简处理后产生的新的特征空间的维度,该维度设置为与实际类标签数目相同.维度约简完成后,使用k-means算法进行聚类,并与实际类标签进行比对,以衡量算法性能.实验结果如表2和表3所示. 表2 ALL-AML数据集上的平均结果 表3 Colon数据集上的平均结果 图1 算法在ALL-AML数据集上的对比结果 图2 算法在Colon数据集上的对比结果 可以看出,我们的算法应用于肿瘤细胞基因数据集时,在准确率和可区分度上,相较已有算法都存在显著的优势. 本文提出了一种基于非负矩阵分解思想,结合图正则化理论和l1/2范数稀疏约束的算法,该方法可以用于对细胞基因表达谱数据进行维度约简.算法结合了已有工作的优势,在保证对数据局部和全局结构的描述能力和对稀疏性的约束能力基础上,针对基因表达谱数据经常存在过度冗余的问题,通过引入去噪处理,大幅提高了算法性能.实验结果证明,算法在基因数据聚类上的表现整体优于传统基于非负矩阵分解的算法. 在使用稀疏约束的NMF方法中,控制稀疏度的参数(本文为λα)大多根据实验经验得来.如何通过理论上的推导和证明,从而合理控制参数以达到最优效果,将是未来一个有价值的研究思路.
3 本文提出的算法
3.1 算法基本模型

3.2 优化过程
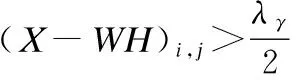


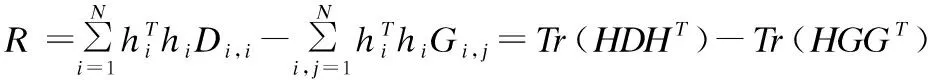

3.3 算法描述
4 实 验
4.1 数据集
4.2 评估指标
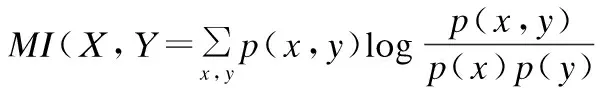




5 结论和展望
