徐 磊 宋安平 刘智翔 张 武

1(上海大学计算机工程与计算科学学院 上海 200444)2(上海海洋大学信息学院 上海 201306)

0 引 言

格子Boltzmann方法LBM是介于流体的微观分子动力学模型和宏观连续模型之间的介观模型。由于Boltzmann方程自身的运动学特性，以及可以根据经典的Chapman-Enskog展开从LBM得到Navier-Stokes方程，使得LBM比基于连续介质假设的Navier-Stokes方程包含了更多的物理内涵。目前，LBM已经应用在了很多流体问题(多项流、湍流、多孔介质以及微尺度流等)中[1-4]。LBM将流体视为比分子大，但在宏观上无限小的一系列粒子。这些粒子按照一定物理规律在网格上进行演化计算，通过对反映粒子状态的分布函数进行统计平均求得宏观物理量。

文献[5-6]首先分别提出了单松弛时间格子Boltzmann模型SRT-LBM(Single-Relaxation-Time LBM)和格子BGK模型LBGK(Lattice Bhatnagar-Gross-Krook)。它们采用单一松弛时间系数，计算效率得到极大提高。尽管SRT-LBM已经被成功地应用于模拟各种流体问题，但是该模型仍然存在缺点：当无量纲松弛时间过于趋近0.5时，模型会产生数值不稳定导致程序发散。针对这一问题，D′Humiéres[7]提出了广义格子Boltzmann模型GLBE(Generalized Lattice Boltzmann Equation)，或称为多松弛格子Boltzmann模型MRT-LBM(Multiple-Relaxation-Time LBM)。2000年-2002年间，文献[8-10]对该模型对该模型二维和三维的物理原理、参数选取、数值稳定性和计算效率等方面进行了详细的理论分析，表明了MRT-LBM的稳定性和精确性都要优于SRT-LBM。

相对于SRT-LBM，MRT-LBM稳定性更高，但是并未克服松驰时间趋近于0.5时计算不稳定导致程序发散的问题。随着雷诺数的增大，MRT-LBM和SRT-LBM虽然都可通过增加网格数保持计算稳定，但是当雷诺数更大时，利用SRT-LBM和MRT-LBM直接数值模拟流场全部动态信息所需要的内存和求解时间非常巨大[11]。为了在模拟湍流场时节省计算耗费并在有限的计算机硬件条件下尽可能完整地给出瞬时流场信息，可在格子Boltzmann模型中引入大涡模拟技术LES(Large Eddy Simulation)[12]。Hou等[13-14]通过非平衡粒子分布函数的二阶矩计算了应变率张量，从而将Smagorinsky涡粘性模型引入SRT-LBM中。而Kxafczyk等[15]则利用传递矩阵将粒子分布函数的二阶矩从速度空间传递到矩空间计算祸粘性系数，将Smagorinsky涡粘性模型与D3Q15 MRT-LBM组合。文献[16-17]通过Chapman-Enskog分析推导应变率张量，分别将Smagroinsky模型引入到D3Q19 MRT-LBM和包含外力项的D3Q19 MRT-LBM中，得到MRT-LBM-LES(MRT-LBM with LES)模型。

如今，计算流体力学研究对象的规模和复杂程度向更大更深的方向发展，单个计算节点不能满足计算需求，需要借助于高性能计算机满足计算的需要。大规模并行计算在一定程度上可以解决计算需要和超级计算性能之间的矛盾。LBM中格点演化主要分为碰撞和迁移两个过程，碰撞是各个格点独自同时进行的，只与格点自身相关。迁移时格点上的粒子也只是与离它们最近格点上的粒子进行信息交换，所以LBM非常适合并行计算。诸多研究人员对LBM的并行性能进行了研究，设计了高可扩展高效率的并行算法。Pan等[19]在不同并行计算平台比较区域划分方法的性能，利用D3Q15模型模拟了单向和多项流在多孔介质中的流动情况。Wu等[20]对高雷诺数二维方腔流，采用域分解方法对D2Q9 MRT-LBM和SRT-LBM进行了比较。Velivelli等[21]利用CPU缓存的优势，将计算区域分块循环计算，加快了计算速度。Schepke等[22]采用块划分策略对SRT-LBM进行了并行性能的分析，该方法使得每个进程都分配到整个计算区域中的一个子计算区域，各个子计算区域与相邻的子计算区域进行数据的传递。文献[23]针对多孔介质内流体流动提出了负载均衡策略减少计算时间。本文主要研究了MRT-LBM引入Smagorinsky涡粘性模型后在大规模并行计算机上的并行性能。

1 MRT-LBM-LES以及边界条件

1.1 MRT-LBM-LES

MRT-LBM将速度空间的碰撞通过线性变换转化为矩空间的碰撞，使得作用后得到的量具有物理意义。在矩空间完成碰撞后，再进行逆变换到速度空间，进行迁移的过程。MRT-LBM的碰撞过程是在矩空间中进行的，它的演化方程为：

f(x+ciδt,t+δt)-f(x,t)=-M-1S[m(x,t)-meq(x,t)]

(1)

式中：f(x,t)是粒子分布函数，M是变换矩阵，m(x,t)=Mf(x,t)是矩空间的粒子分布函数，meq(x,t)是矩空间的平衡态分布函数。S是松弛对角阵，并且S对角线各项满足0≤Si<2。

式(1)可以分为碰撞和迁移两个过程:

f(x,t)=f(x,t)-M-1S[m(x,t)-meq(x,t)]

(2)

f(x+ciδt,t+δt)=f(x,t)

(3)

常用的二维LBM模型为D2Q9(如图1所示)。它的离散速度为:

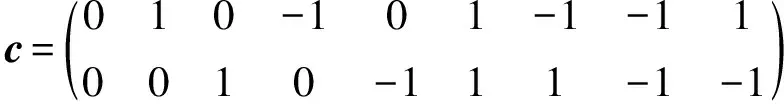
(4)

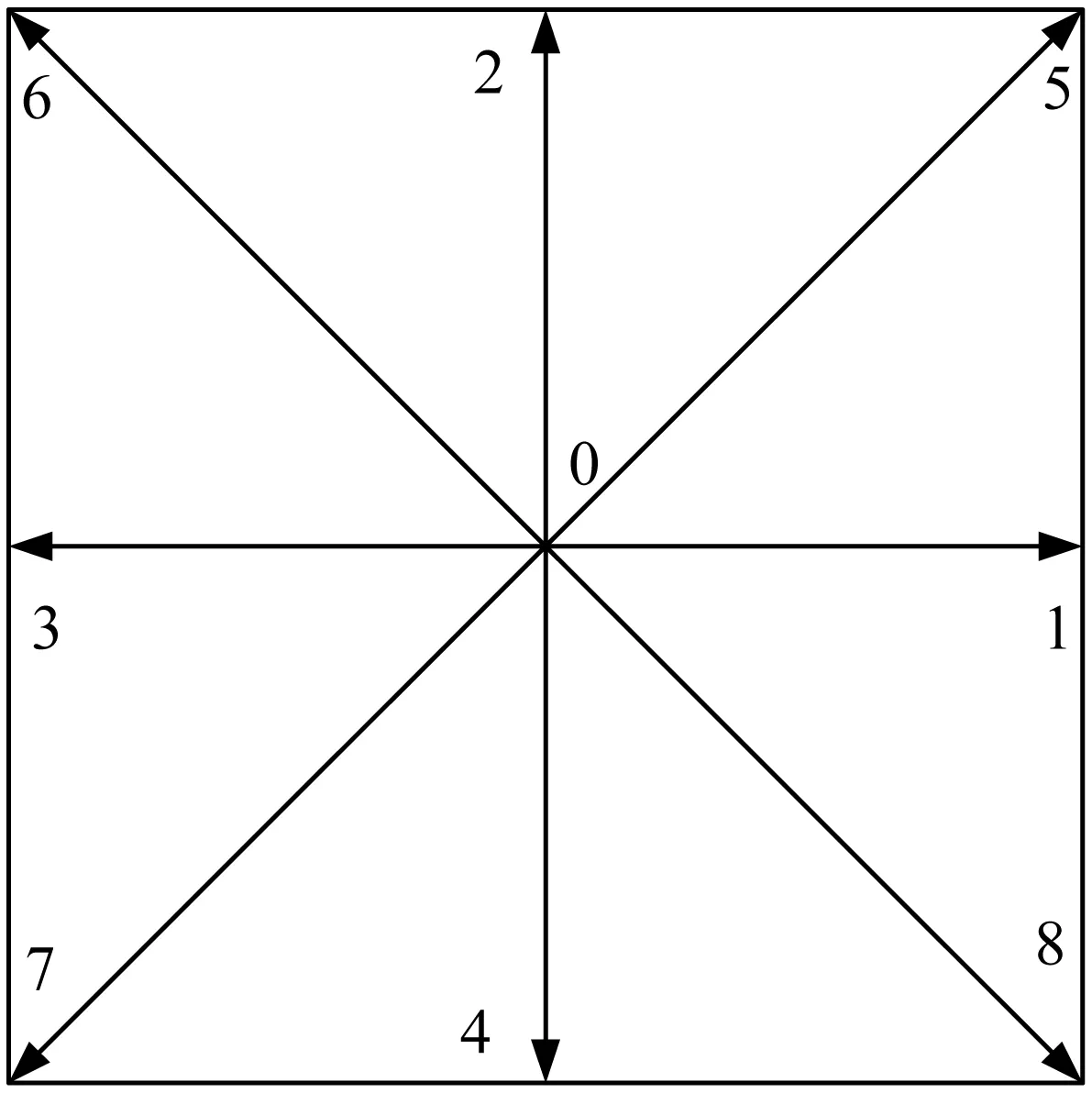
图1 D2Q9

平衡态分布函数:

(5)

(6)

D2Q9对应的变换矩阵:

(7)

矩空间的平衡态分布函数meq为:

meq=ρ(1,-2+3u2,α+βu2,ux,-ux,uy,-uy,

(8)

式中:α和β为自由参数，ρ为密度，u为速度。松弛矩阵diag(0,se,sε,0,sq,0,sq,sv,sv)。剪切粘性和体粘性系数分别为：

(9)

(10)

宏观量为:

ρ=∑fi

(11)

(12)

为了能够模拟湍流，Hou等[13]将Smagroinsky模型引入到D2Q9中。在引入的Smagorinsky模型中，无量纲的运动粘性系数v由分子运动粘性v0和涡粘性vt组成:

υ=v0+vt

(13)

式中：vt由应变率张量Sαβ，参数Cs以及格子步长δx决定,其表达式如下：

vt=(Csδx)2|Sαβ|

(14)

1.2 边界条件

在处理曲面复杂边界时，如果使用平直边界的边界处理方法，精度较低。为此，Yu等[24]提出了一种曲面边界的处理方法。如图2所示，实心圆表示固体点，空心圆表示流场点，曲线表示实际的物理边界，它将流场分为固体点和流场点，方格点为边界节点。

图2 曲面边界

这里将流场点记为xf，固体点记为xb，与xf相邻的流场点记为xff，边界点记为xw。则流场点xf的分布函数为：

(15)

(16)

对于平直边界，本文采用Guo等[25]提出的非平衡态外推方法。

2 格子类型的判断

当流场中物体存在复杂边界时，需要判断物体附近格子点的类型，通过不同类型的格子点计算出物体边界处的格子点粒子分布函数。本文通过射线法判断格子的类型。从待判断点的某一个方向引射线，计算和物体边界的交点个数，通过交点个数的奇偶性得到格子点的类型。本文使用圆柱和Rae2822翼型为例判断格子点的类型，如图3和图4所示。该方法可以准确的判断出圆柱和翼型流场中的格子类型。

图3 圆的格子类型(包括固体点和边界点)

图4 Rae2822翼型的格子类型(包括固体点和边界点)

3 并行策略

对于二维问题，流场可以沿着一个方向或两个方向进行划分。当并行环境中核数增多时，沿着一个方向进行划分并不符合实际问题的需要，所以本文选择沿着两个方向对流场进行划分。在进行并行处理时，每个MPI进程负责处理一个流场的子区域，每个子区域用一个二元组(i,j)标记。进程总数记为n。二元组可以通过下式获得：

i=mod(n,nx)

(17)

(18)

式中：nx为沿着x方向的划分数。每个子区域的范围为:

(19)

(20)

式中：nLx是x方向格子点数，xmin是子区域的起始格点位置，xmax是子区域的结束格点位置。子区域在y方向的范围可以类似计算得到。

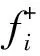
图5 进程(i,j)传递部分数据给进程(i+1,j)

图6 流场中各个子区域信息传递

4 数值实验

4.1 数值验证

为了验证本文并行算法的正确性，我们使用圆柱和翼型在流场中的情况分别进行了测试。流场的速度为U=0.115 5。图7中，(a)和(b)是圆柱绕流雷诺数Re=20和40时的流线图，从图中可以看出，在圆柱后产生了一对对称的涡，随着雷诺数的增大，涡也在逐渐变大。(c)和(d)是雷诺数Re=100和150时的流线图，圆柱后方两侧的涡随着雷诺数的增大开始出现震荡，当超过临界值时，圆柱后的涡逐渐分离，形成周期性交替脱落、旋转方向相反的非对称涡[26]。

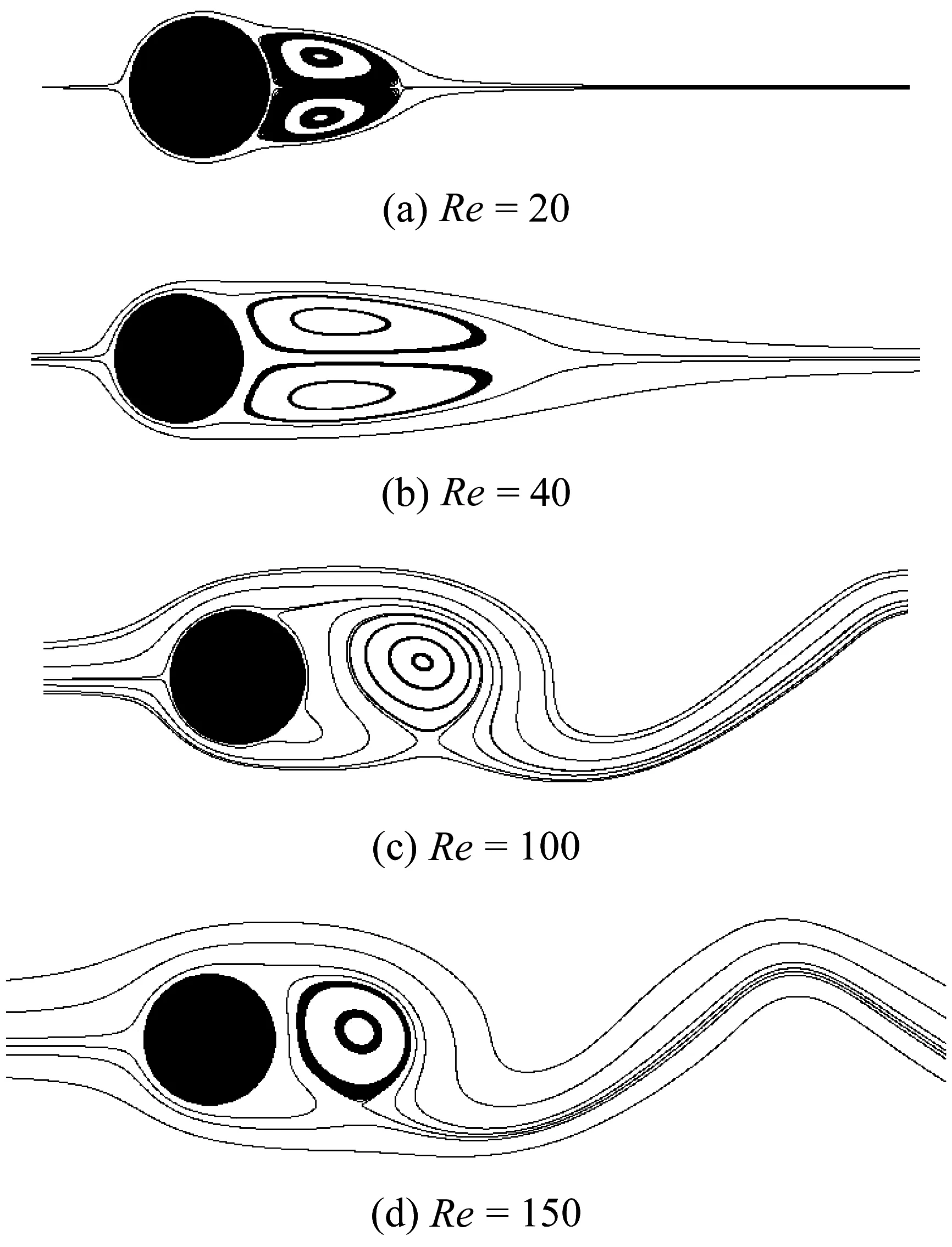
图7 圆柱绕流流线图

图8中的(a)和(b)是翼型绕流雷诺数Re=100 000时的流线图，(a)的攻角为0°，(b)的攻角为3°。可以看出，实验结果与文献[27]一致。

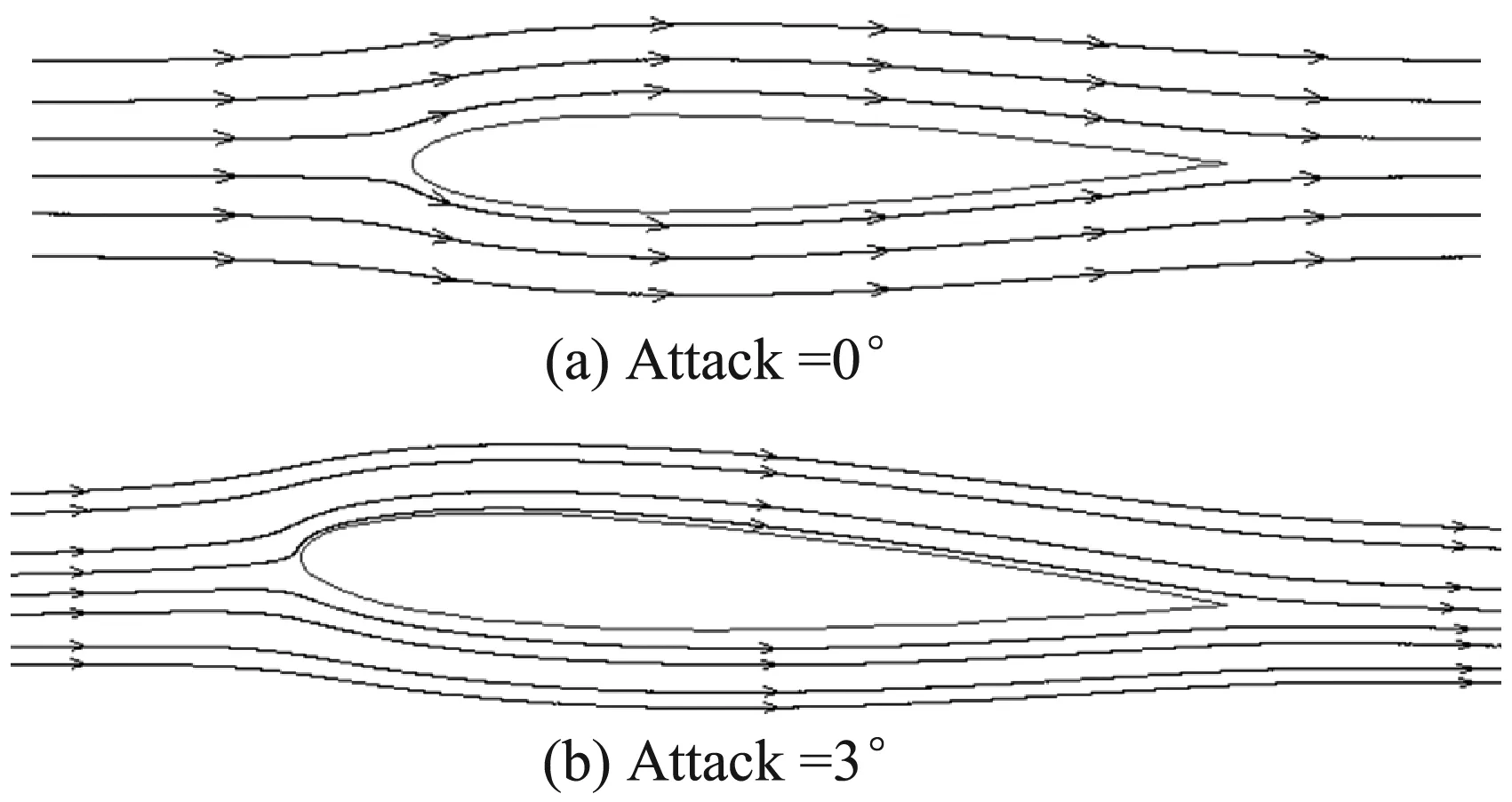
图8 翼型绕流涡量图

4.2 效率验证

本节基于128核集群进行并行性能的测试，该集群包含1个登录节点、8个计算节点，每个节点有16个核，配置了两块2×Intel Xeon E5-2660 CPU。每个节点的内存为128 GB。节点之间通过56 GB Infiniband线连接。

为了统计程序运行时间，进行了500步迭代。采用了1 000×1 000和1 500×1 500两种格子规模进行了加速比和效率的测试，比较了两种不同规模下的加速比和效率。

分别在核数为8、16、32、64以及128核上进行了时间的统计。图9为两种不同格子规模下加速比的比较，圆形为格子规模1 500×1 500的加速比，正方形为格子规模1 000×1 000的加速比，黑色直线为理想加速比。可以看出，两种格子规模的加速比都呈直线上升，格子规模较大的加速比要略高。由于进程之间需要进行边界上格子信息的通信，加速比要低于理想加速比。因为进程间的通信量只发生在相邻进程间，并没有大规模的主从式通信，所以加速比基本为直线。

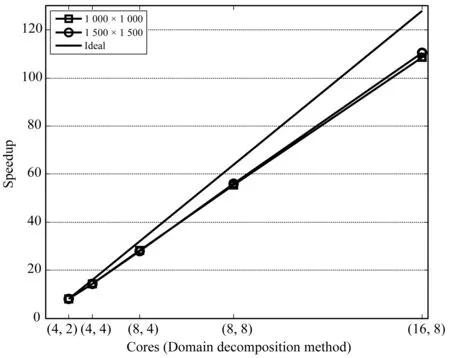
图9 加速比

图10为两种不同规模下效率的比较，圆形为格子规模1 500×1 500的效率，正方形为格子规模1 000×1 000的效率。可以看出，两种格子规模的效率都在缓慢下降，随着核数的增加，格子规模较大的效率下降趋势更为缓慢，当核数达到128核时，计算效率可以达到86.5%。从图9和图10可以看出，我们所实现的并行算法有良好的可扩展性。

图10 效率

5 结 语

本文提出了一种高可扩展的格子Boltzmann方法。该方法可以有效判断格子类型，模拟高雷诺数下流场中的湍流，采用双向的区域分解方法，并设计了详细的划分策略以及数据交换策略，大大降低了通信量，减少了通信时间。数值结果表明，该算法具有良好的可扩展性，效率可以在128个核心上达到86.5%。