周 鑫, 刘 静, 汤建钢

(1. 伊犁师范学院 数学与统计学院, 新疆 伊宁 835000; 2. 东北师范大学 数学与统计学院, 长春 130024;3. 伊犁职业技术学院 基础部, 新疆 伊宁 835000)

模糊集[1]用于刻画客观事物的不确定性. 设X是一个非空集合, 集合X的模糊子集可由隶属函数A:X→[0,1]刻画, 其中:X称为A的承载集, 记为K(A)=X; [0,1]称为真值集. 为了使模糊集能刻画更一般的事物, Goguen[2]引入了L-fuzzy子集的概念, 其真值集由比[0,1]更一般的完全分配格L代替.

由模糊集合的分解定理知, 一个模糊集对应一族集合. 反之, 由模糊集的表现定理知, 一族集合可形成一个模糊集. Gentilhomme[3]定义了一种刻画模糊集的非经典集合——flou集的概念; 文献[4]给出了L-flou集的概念及性质, 并得到了L-fuzzy集与L-flou集的格同构关系. 文献[5]研究表明,L-flou集可用集合套表现, 使其表示模糊信息时既增强了模糊信息的表达精度, 又避免了单点隶属度确定困难的问题. 基于此,L-flou集理论在处理信息等领域应用广泛.

本文利用范畴理论, 将真值集L视为范畴L, 给定元素的隶属度视为范畴中的对象, 用态射刻画不同隶属度之间的关系, 给出L-fuzzy集范畴Set(L )与L-flou集合范畴Set(fL )的同构关系, 并结合文献[6-7], 得到了范畴Set(fL )同构于赋予层结构的集合范畴SetL(S H ).

1 预备知识

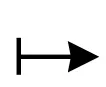
定义1[2]设X∈Ob(Set), 函数A: X→L称为集合X的L-fuzzy子集, 也称为L-子集或L-集, 记做(X,A). 在承载集合X确定且不至引起混淆的情况下, 简记为A.

注1按点态方式定义集合X的所有L-fuzzy子集, 表示为FL(X)={A|A: X→L }=LX, 其构成完备的Heyting代数[2,8].

定义2[4]设X∈Ob(Set), 若集值函数μ: Lop→P (X)满足:

1) μ(0)=X;

则μ称为集合X的L-flou子集, 记作(μ,X). 集合X的所有L-flou子集表示为

F lL(X)={μ: L → P (X)|μ满足1),2)}.

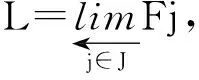
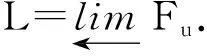
图1 F上的余锥形Fig.1 Cocone on F

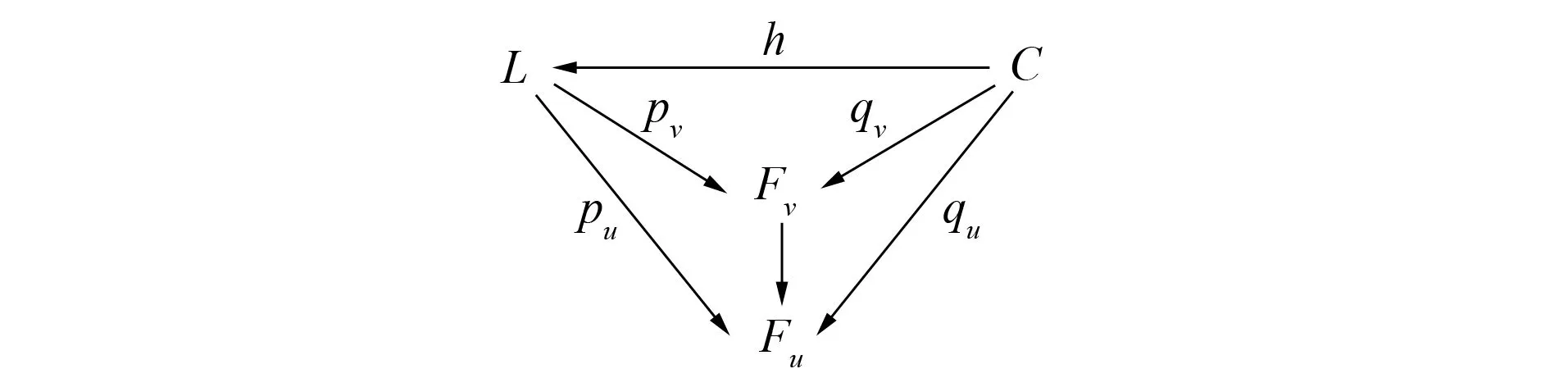
图2 F的余极限Fig.2 Colimit of F

定义4[9]如果范畴C中任意J型图都存在极限, 则称C为完备范畴. 对偶地, 可定义余完备范畴.

定义5[10]设C是一个范畴, 取X∈Ob(C ), 定义范畴C/X如下：

1) 对象: 任意C∈C, 范畴C中态射f: C→X作为C/X的对象;

2) 态射: 对于f: C→X, g: D→X, 定义Hom(f,g)={h∈Hom(C,D)|f=gh};

3) 复合: 由范畴C中复合诱导;

4) 单位: 1f=idX.

则称范畴C/X为对象X上的切片范畴. 对偶地, 可定义余切片范畴X/C.

定义6[8]设C是一个完备范畴, L上的一个C-预层F是范畴Lop到范畴C的函子F: Lop→C, 则：

1) 对象间的对应: 若u∈Ob(L ), 则F(u)∈C;

2) 态射间的对应: 若v≤u∈Mor(L ), 则F(v≤u): F(u)→F(v)∈Mor(C ).

定义7[8]设F是L上的一个C-预层, {ui|i∈I}, {u=∨ui|i∈I}(ui∈L ), 如果

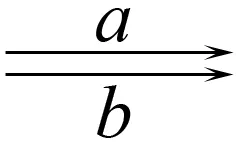
正合, 即态射e是态射a,b的等值子, 则称F是L上的一个C-层.

注2特别地, 取范畴C为Set, 则可得集合范畴上的预层及层.

2 范畴Set(L )与范畴Set(fL )的同构关系

定义8设L是一个完备格范畴, Set是集合范畴, 则L-fuzzy集合范畴Set(L )定义如下:

1) 对象: 序对(X,A), 其中X∈Ob(Set), A: X→L为集合X的L-fuzzy子集;

2) 态射: 序对(f,f*): (X,A)→(Y,B), 其中f: X→Y, f*: A→B由f诱导且满足A≤B∘f;

3) 复合: 集合映射的复合诱导;

4) 单位: 对任意对象(X,A), 有1(X,A)=(1X,1A).

注3由定义3及文献[11-12], 可定义范畴Set(L )中的极限及余极限等相关概念.

定义9设L是一个完备格范畴, Set是集合范畴, 则L-flou集合范畴Set(fL )定义如下:

1) 对象: 对(μ,X), 其中X∈Ob(Set), μ: L→P (X)为集合X的L-flou子集;

3) 复合: 若φ: (μ,X)→(ν,Y), ψ: (ν,Y)→(ω,Z), 则ψ∘φ: (μ,X)→(ω,Z)满足

(φ*∘ψ*)∘μ=(φ∘ψ)*∘μ≤ω;

4) 单位: 对任意对象(X,A), 有1(X,A)=(1X,1A).

注4可将L-flou集合范畴Set(fL )视为函子范畴, 即

其中X的幂集合P (X)可视为偏序范畴, 其对象为集合X的子集合, 态射为集合间的包含关系.

定理1设L是一个完备格范畴, Set是集合范畴, 则L-fuzzy集合范畴Set(L )同构于L-flou集合范畴Set(fL ).

证明: 构造从范畴Set(L )到范畴Set(fL )的函子F: Set(L)→Set(fL ), 证明其作用在对象类上同构且局部单与局部满. 设函子F: Set(L )→Set(fL ), 则：

1) 对象间的对应: 若A∈Ob(Set(L )), 则F(A)=μA∈Ob(Set(fL )), 这里μA(u)={x∈X|A(x)≥u, u∈L };

2) 态射间的对应: 若f*: A→B∈Mor(Set(L )), 则F(f*)=μf*: μA→μB∈Mor(Set(fL )).

首先证明F作用在范畴Set(L )的对象到范畴Set(fL )的对象上是同构的. 对任意μA∈Ob(Set(fL )), 令Aμ∈Ob(Set(L )), Aμ(x)=∨{v∈Ob(L )|x∈μ(v)}. 为简便, 记{v∈Ob(L )|x∈μ(v)}=Ix.

首先，对于城市居民来说，判断他们与外来人口社会距离的大小其实很简单，那就是利益的重合。如果她们的利益与迁移人口没有重合，也就是说他们的利益不会受到影响时，社会距离就比较小；相反，当城市居民觉得自身的利益会受到外来迁移人口的影响而有所损失时，就会排斥迁移者，从而有着较大的社会距离。体现在本次研究中，就是那些有着更高的收入和主观社会经济地位的城市居民与外来迁移人口的社会距离更近。因为相对于外来迁移人口，他们有着无法比拟的竞争优势，而那些收入较少、主观社会经济地位低，再加上年龄较大的城市居民则更容易体会到来自外来迁移人口的竞争，因此对他们有所排斥。

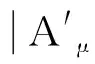
{x∈X|A(x)≥A(x0)=A′(x)≥A(x0)},

从而A′(x0)≥A(x0). 又{x∈X|A(x)≥A′(x0)=A′(x)≥A′(x0)}, 进而A(x0)≥A′(x0), 故A′=A. 综上, F是单的.

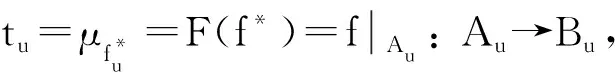
对任意v≤u∈Ob(L ), t对应如图4所示的分支之间的交换性. 由图3的交换性可得图4的交换性, 故t: μA→μB∈Mor(Set(fL )).

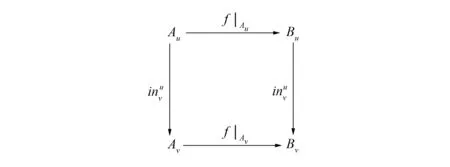
图3 交换图Fig.3 Commutative diagram

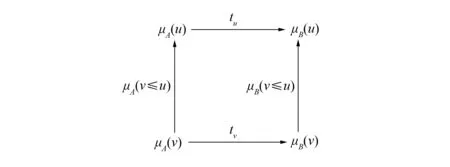
图4 自然变换t的u,v分支Fig.4 Components u,v of natural transformation t

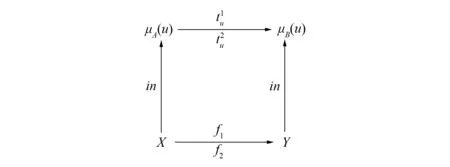
图5 自然变换t的u,0分支Fig.5 Components u,0 of natural transformation t

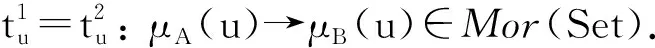
A1,μ=∨{v∈Ob(L )|x∈μA(v)=A2,μ},

故f1*=f2*.

2) 证F局部满. 令

Aμ(x)=∨{u∈Ob(L )|x∈μA(v)},

Bμ(x)=∨{u∈Ob(L )|f(x)∈μB(v)},

可得

故(f,f*): (X,A)→(Y,B)∈Mor(Set(L )).

综上, 函子F是从范畴Set(L )到范畴Set(fL )的同构函子.

3 L-子对象与层

定义10[9]设C是一个完备范畴, 如果对任意Z∈Ob(C )及f,g: Z→X∈Mor(C ), 由if=ig, 有g=h, 则称i: X→Y∈Mor(C )为单态射.

考虑(X′,i), 其中X′∈Ob(C ), i: X′→X∈Mor(C )是单态射.

定义11[9]如果存在f: X′→X″∈Mor(Set), 使得j∘f=i成立, 则(X′,i)≤(X″,j). 若g: X″→X′∈Mor(Set), 使得i∘g=j,j∘f=i, 则称(X′,i)与(X″,j)等价, 记作(X′,i)～(X″,j).

定义12[9]序对(X′,i)在等价关系～下的等价类称为X的子对象. 在不混淆的情形下, 用(X′,i)表示X的一个子对象, 其中i: X′→X是单态射.

命题1[9]设X∈Ob(C ), X的所有子对象构成的范畴记作Sub(X), 则：

1) 对象: X的子对象(X′,i)；

2) 态射: f: (X′,i)→(X″,j), 且i=j∘f;

3) 复合: 对于f: (X′,i)→(X″,j), g: (X″,j)→(X‴,k), 有g∘f: (X′,i)→(X‴,k), 且i=k∘(g∘f)；

4) 单位: 1f= id(X′,i).

定义13设X∈Ob(C ), X的L-子对象是指函子μ: L→Sub(X)满足:

1) μ(0)=X;

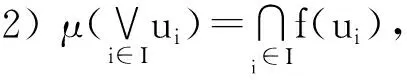
注6当X∈Ob(Set)时, X的L-子对象即为X的L-子集.

定义14[6]设X∈Ob(Set), 函子F: Lop→Sub(X)是Sub(X)层, 则称F是X上的一个层结构, (X,F )称为赋予层结构的集合.

定义15赋予层结构的集合范畴SetL(S H )定义如下：

1) 对象: 赋予层结构的集合(X,F )；

2) 态射: (X,F ), (Y,G)赋予层结构的集合, 态射(f,t): (X,F )→(Y,G)中f: X→Y∈Mor(Set), t: F→G是自然变换;

3) 复合: (f,t)∘(g,s)=(f∘g,t∘s);

4) 单位: 1(X,F )=(1X,1F).

定理2设L是一个完备格范畴, 则赋予层结构的集合范畴SetL(S H )同构于L-flou集合范畴Set(fL ).

证明: 由文献[6]知, 赋予层结构的集合范畴SetL(S H )同构于L-fuzzy集合范畴Set(L ). 再由定理1可得结论.