☉山东省泰安第一中学 李晓楠

在近年的高考题与模拟题中，经常会碰到求解双变元或多变元的代数式的最值或取值范围问题.此类问题往往难度较大，思维方式多变，方法有时也多样.多做题不如精做题，当我们解完一道题以后，要不断领悟反思，多角度切入进行深度挖掘，以求达到触类旁通、一题多解的效果.下面结合一道双变元代数式的最值题来加以实例剖析，多角度切入，来体会其异曲同工之妙.

【问题】已知实数x，y满足x2+2xy-1=0，则x2+y2的最小值为______.

分析：这是一道双变元在已知条件下求其代数式的最值问题，这类问题一直受备命题者的青睐.通过认真审视这道题，在不同视角下，得到了该题的不同解题思维与对应的精彩解法.

思维角度1：结合已知关系式进行因式分解，通过对关系式x+2y进行换元，得到x、y关于新参数的关系式，代入所要求解的代数式，通过变形，利用基本不等式进行求解.对已知等式进行因式分解，采用换元法，可以简化运算，提升效益.

思维角度2：结合已知关系式得到x2+2xy=1，通过基本不等式法的转化，并结合所要求解的结果进行对比系数得到关系式1+=t，求解参数t的值并代入不等式，通过不等式的性质来转化即可确定对应的最值问题.

解法2（基本不等式法）：由于x2+2xy-1=0，则有x2+2xy=1，结合基本不等式有1=x2+2xy≤x2+x2+ty（2其中参数t＞0），当且仅当x2=ty2时，等号成立，结合系数关系

思维角度3：结合已知关系式得到x2+2xy=1，设x2+y2=t（t＞0），进而建立关系式x2+y2=t（x2+2xy），转化为关于x的一元二次方程，利用函数与方程，结合判别式来确定最值问题.

解法3（二次方程法）：由于x2+2xy-1=0，则有x2+2xy=1，设x2+y2=t（t＞0），则有x2+y2=t（x2+2xy），整理有（1-t）x2-2tyx+y2=0，由以上关于x的一元二次方程有实数根，可得1-t≠0且Δ=4t2y2-4（1-t）y2≥0，整理有t2+t-1≥0，解得t≥

思维角度4：结合已知关系式得到x2+2xy=1，通过代数式x2+y2的除“1”转化为分式，结合参数t=的引入，通过转化相应的分式，结合基本不等式来确定相应的最值问题.

思维角度5：根据所要求解的代数式的形式进行三角换元x=rcosα，y=rsinα，代入已知关系式并分离参数r，结合三角恒等变换，并利用三角函数的图像与性质来确定相应的最值问题即可.

解法5（三角换元法）：由于x2+2xy-1=0，则有x2+2xy=1，设x=rcosα，y=rsinα，则有r2cos2α+2r2sinαcosα=1，整理可

思维角度6：结合已知关系式得到x2+2xy=1，设出x2+y2=r2，进而结合三角换元思维代入关系式1=x2+2xy，通过三角恒等变换，并利用三角函数的图像与性质来确定相应的最值问题，再结合不等式的性质即可求解.

解法6（三角换元法）： 设x2+y2=r2，则有x=rcosα，y=rsinα，

由于x2+2xy-1=0，则有x2+2xy=1，

思维角度7：根据x2+2xy-1=0，引入参数t与0的乘积作差，转化为二次函数，通过配方，并根据使得不等式成立时对应的系数比较建立参数t的根式方程，通过求解根式方程来确定相应的最值问题即可.

解法7（比较系数法）：由于x2+2xy-1=0，所以x2+y2=x2+y2-（tx2+2xy-1）=（1-t）x2-2txy+y2+t=（x-y）2+t≥t，要使得以上不等式成立，只要2t=2，解得t=不满足根式方程，舍去），所以

思维角度8：结合极坐标的几何意义知x2+y2=ρ2表示的是曲线x2+2xy-1=0上的点到坐标原点的距离的平方，进而结合极坐标公式代入关系式1=x2+2xy，通过三角恒等变换，并利用三角函数的图像与性质来确定相应的最值问题，再结合不等式的性质即可求解.

解法8（极坐标法）：根据极坐标方程可知x2+y2=ρ2，其表示的是曲线x2+2xy-1=0上的点到坐标原点的距离的平方，

而 x=ρcosθ，y=ρsinθ， 所 以 1=x2+2xy=ρ2cos2θ+

思维角度9：结合x2+2xy-1=0得到曲线结合x2+y2=r2表示的是曲线的距离的平方，通过求导，并结合圆的切线方程，建立对应切线的斜率相等，进而得到切点（x0，y0）所对应的值，从而可知x2+y2=r2≥x02+y02来确定相应的最值问题即可.

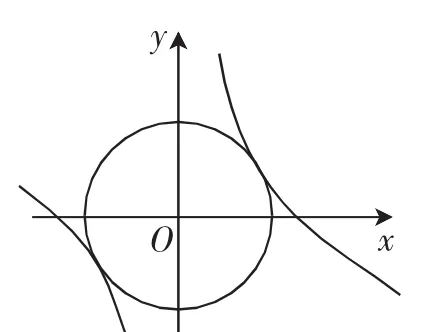
图1

解法9（数形结合法）：由x2+y2=r2，其表示的是曲线上的点到坐标原点的距离的平方，结合图1可知当曲线x2+y2取得最小值，此时切点为（x0，y0）（不失一般性，取切点位于第一象限内），由过切点（x0，y0）的切线的斜率为y2=r2上，过切点（x0，y0）的切线方程为x0x+y0y=r2，此时

总结：解决此类两变元的二次代数式问题，往往根据条件对已知等式进行转化或处理，将所要求解的双变元的二次代数式利用换元思维、基本不等式思维、方程思维、三角函数思维以及其他相关的思维方式加以转化，再结合相关的知识加以解决.

著名数学家、教育学家G·波利亚在《怎样解题》一书中指出：“好题目和某种蘑菇有点相似之处：它们都是成串成长，找到一个以后，我们应该看看，很有可能在很近的地方又能找到更多的.”通过典型实例的一题多解，可以使得我们的解题思路更加开阔，数学知识的掌握更加熟练，同时思维拓展，妙法顿生，提高解题速度，培养发散思维能力，有助于激发我们学习的主动性、积极性和趣味性，从而全面提高我们的知识水平和思维能力.J