几类张量空间的乘积基的结构
2018-04-20唐西林刘燕娜
唐西林,刘燕娜
(华南理工大学数学学院,广东广州510640)
由于相互无偏基在量子通信中起着重要作用,因此引起了人们对相互无偏基的关注。已知复向量空间Cd的相互无偏基个数小于等于d+1,当d为素数的方幂时,相互无偏基的个数可取得最大值[1]。然而,当d≥6且d为合数时,上界是否可以取得仍然是一个公开问题。特别地,当维数为6时,尚不清楚是否有超过3个相互无偏基,但这3个相互无偏基都是二体系统的乘积基的形式。基于这一情况,很多研究者开始研究相互无偏乘积基[2-4]。2012年,Mcnulty等[3]讨论了d=4,6的所有乘积基,且提出了局部等价变换的定义。2016年,Mcnulty等[2]提出了关于二体系统的乘积基的结构猜想。2017年,笔者刻画了d=2n 的乘积基的结构[5]。
猜想 1[2]集合是空间 d1⊗d2的一组正交乘积基,当且仅当,|ai〉∈Cd1(i=1,2,…,d)这d个向量和|bi〉∈Cd2(i=1,2,…,d)这d个向量分别被拆分为Cd1的d2组正交基和Cd2的d1组正交基。
定义1[6]如果B中的每一个元素都是纯乘积向量,那么复向量空间的一个正交基B称为乘积基,其中 d=d1d2…dm。
1 m⊗n的乘积基的结构
引理1空间3⊗3的任意正交乘积基等价于以下族的其中一个

(1)当|a1〉重数为3,B中第1个系统的态与|a1〉正交的态的个数小于等于5时,乘积基B=在|bi〉,i=4,5,…,9 中,总能找到一个态|bi〉需要与 C3的正交基正交,矛盾。因此当|a1〉重数为3时,只需要考虑B中第 1 个系统的态与|a1〉正交的态的个数等于 6 的情况。令i=5,6,…,9。
考虑|ai〉,i=5,6,…,9与|a1⊥〉正交的个数,当正交的个数为4或5时,至少有4个态相等,因此乘积基不存在。
当|ai〉,i=5,6,…,9 与|a1⊥〉正交的个数为 3 时,分析可以得到以下乘积基

当|ai〉,i=5,6,…,9 与|a1⊥〉正交的个数为 2 时,只有当|ai〉,i=7,8,9 与|a1⊥⊥〉正交的个数为 1时,存在以下正交乘积基
当|ai〉,i=5,6,…,9 与|a1⊥〉正交的个数为 1 时,|ai〉,i=6,7,8,9 与|a1⊥⊥〉都不正交时,考虑|ai〉,i=,7,8,9 与|a6〉的正交关系,当〈ai|a6〉≠0,i=7,8,〈a9|a6〉=0 时,乘积基为

其中,|ai〉=αi-1|a1⊥〉+βi-1|a1⊥⊥〉,|ai⊥〉=βi-1|a1⊥〉-αi-1|a1⊥⊥〉,αi-12+βi-12=1,i=2,3。当〈a7|a6〉≠0,〈ai|a6〉=0,i=8,9 时,乘积基存在为中总能找到至少 4 个态|bi〉相等,这与C3中的态至多有3个相同矛盾。因此当|a1〉重数为2时,只需要考虑B中第1个系统的态与|a1〉正交的态的个数等于4至6个的情况。

当|a1〉重数为2时,考虑B中第1个系统的态与|a1〉正交的态的个数等于4的情况,由〈bi|b1〉=〈bi|b1⊥〉=0,i=7,8,9 得|bi〉=|b1⊥⊥〉,i=7,8,9,则

当|ai〉,i=5,6,…,9 与|a1⊥〉正交的个数为 0 时,不存在正交乘积基。
(2)当|a1〉重数为2,B中第1个系统的态与|a1〉正交的态的个数等于2或者3时,乘积基B=
βi-2|b1⊥〉,αi-22+βi-22=1,i=3,4,5,6。
②若〈ai|a1⊥〉≠0,i=4,5,〈a6|a1⊥〉=0,则0时,乘积基不存在。当〈b4|b6〉=0时,乘积基为


④若〈ai|a1⊥〉=0,i=4,5,6,此时正交乘积基不存在。
当|a1〉重数为2,B中第1个系统的态与|a1〉正交的态的个数等于5时,满足条件的正交乘积基有



当|a1〉重数为 2,B 中第 1 个系统的态与|a1〉正交的态的个数等于 6 时,由〈b9|b1〉=〈b9|b1⊥〉=0 得|b9〉=|b1⊥⊥〉。令|a3〉=|a1⊥〉,当|ai〉,i=4,5,…,8 与|a1⊥〉正交的个数大于等于 0 时都不能组成乘积基。
(3)当|a1〉重数为1,B中第1个系统的态与|a1〉正交的态的个数等于2或者3时,表明B中第2个系统的态与|b1〉正交的态的个数为6或5,由于空间3⊗3是对称的,因此只需要对乘积基调换第1个系统与第2个系统的态即可,因此不需要讨论。
当|a1〉重数为1,B中第1个系统的态与|a1〉正交的态的个数等于4时,满足条件的正交乘积基有



当|a1〉重数为1,B中第1个系统的态与|a1〉正交的态的个数等于5或6时,不存在正交乘积基。
2 多体系统的乘积基的结构
由于二体系统2⊗n的乘积基中,第1个系统的态及第2个系统的态分别可以被拆分为C2的n组正交基和Cn的2组正交基。对于Cn这一子系统,如果n可以拆分成2×m的形式,也就是说,考虑系统2⊗n等价于考虑系统2⊗2⊗m。如果已知2⊗m的所有乘积基,那么可以构造2⊗n的所有乘积基。下面以2⊗2⊗2为例进行说明。我们猜想这种方法可以推广到空间2⊗k⊗3⊗l。

其中A(ci)={|aj,bj〉||ci〉⊗|aj〉⊗|bj〉∈B,j=1,2,…,4n},A(ci⊥)={|aj,bj〉||ci⊥〉⊗|aj〉⊗|bj〉∈B,j=1,2,…,4n}。
根据上面的分析,只需要考虑r=4,3,2,1这4种情况。
情形 1 若 r=4,则乘积基为 C={|ci〉⊗ Ai,|ci⊥⊗ Di|i=1,2,3,4},且{Ai|i=1,2,3,4}及{Di|i=1,2,3,4}都为 2⊗2 的乘积基,又因为 2⊗2 的所有乘积基必须为以下 B0,B1,B2的形式[3]


情形 2 若 r=3,则乘积基为 C={|ci〉⊗ Ai,|ci⊥〉⊗Di|i=1,2,3},且{Ai|i=1,2,3}及{Di|i=1,2,3}都为2⊗2的乘积基。

情形 3 若 r=2,则乘积基为 C={|ci〉⊗Ai,|ci⊥〉⊗ Di|i=1,2},且{Ai|i=1,2}及{Di|i=1,2}都为 2⊗2的乘积基。
当{Ai|i=1,2}和{Di|i=1,2}这两组基相同时,2⊗2⊗2的乘积基分别为
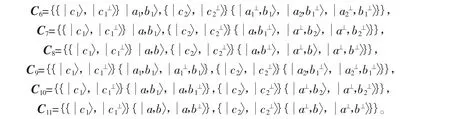
当{Ai|i=1,2}和{Di|i=1,2}这两组基不相同时,有 4 种情况可以组成乘积基。当 i=1,2,Ai只包含一个元素,而Di包含3个元素时,B0,B1,B2这三组基中任取两个都可以构造出乘积基;当i=1,2,Ai和Di都包含2个元素时,只有当{Ai|i=1,2}=B1,{Di|i=1,2}=B2时可以构造出乘积基,其他情形都不能构造出乘积基。因此这种情况下,2⊗2⊗2的乘积基有

情形 4 若 r=1,则乘积基为 C={|c1〉⊗A1,|c1⊥〉⊗ D1},且 A1及 D1都为 2⊗2 的乘积基。
当A1和D1这两组基相同时,2⊗2⊗2的乘积基分别为

当A1和D1这两组基不相同时,2⊗2⊗2的乘积基分别为

由上述分析可得,2⊗2⊗2的所有乘积基有C0,C1,…,C21这22种情形。
推论 3 令 B={|ci,ai,bi〉|i=1,2,…,8}为复向量空间 2⊗2⊗2 的正交乘积基。则|ai〉(i=1,2,…,8)这8 个向量,|bi〉(i=1,2,…,8)这 8 个向量及|ci〉(i=1,2,…,8)这 8 个向量都可拆分为 C2的 4 组正交基。
通过对2⊗2⊗2的乘积基分析、计算,可得到2⊗2⊗3的乘积基包含65种情形,且得到以下结论:
推论 4 令 B={|ci,ai,bi〉|i=1,2,…,12}为复向量空间 2⊗2⊗3 的正交乘积基。则|ai〉(i=1,2,…,12)这 12 个向量,|ci〉(i=1,2,…,12)这 12 个向量都可以拆分为 C2的 6 组正交基,|bi〉(i=1,2,…,12)这 12个向量可以拆分为C3的4组正交基。
由推论2及推论3,我们猜想对于空间2⊗k⊗3⊗l也有以下相应的结论:
猜想2 令B为复向量空间2⊗k⊗3⊗l的正交乘积基。则子系统C2的态都可以拆分为C2的2k-1×3l组正交基,子系统C3的态都可以拆分为C3的2k×3l-1组正交基。
参考文献:
[1]WOOTTERS WK,FIELDS B D.Optimal state-determination bymutually unbiased measurements[J].Annals ofPhysics,1989,191(2):363-381.
[2]MCNULTYD,PAMMER B,WEIGERTS.Mutuallyunbiased product bases for multiple qudits[J].Journal ofMathematical Physics,2016,57(3):1-11.
[3]MCNULTY D,WEIGERTS.All mutuallyunbiased product bases in dimension 6[J].Journal ofPhysics A:Mathematical and Theoretical,2012,45(13):1-22.
[4]WIENIAK M,PATEREK T,ZEILINGER A.Entanglement in mutually unbiased bases[J].NewJournal of Physics,2011,13(5):1-24.
[5]唐西林,刘燕娜,谷泽.C2⊗Cn的乘积基的结构[J].佛山科学技术学院学报(自然科学版),2017,35(1):19-23.
[6]ALONN,LOVASZL.Unextendible product bases[J].Journal ofCombinatorial Theory:Series A,2001,95(1):169-179.
