杜江珊, 李占山

(吉林大学 计算机科学与技术学院, 符号计算与知识工程教育部重点实验室, 长春 130012)

约束满足问题(constraint satisfaction problems, CSP)[1]是人工智能领域中的重要研究方向, 而求解CSP问题的最有效方法为将相容性算法[2]与搜索算法相结合的回溯搜索算法(MAC)[3]. 随着CSP求解问题的深入研究, 多种高效、 表示方式丰富的算法被提出. 其中, 由于表约束在表达上简洁、 方便, 因此基于表的相容性算法求解技术[4]被广泛应用. 对于表约束, 许多经典的过滤算法都是在运行过程中, 通过推断出工作在保持不变的约束上减少检索的. 但在近年研究中, 提出了一种去除遍历不相关元组的方式, 达到减少遍历次数, 最终提高检索效率的效果[5]. STR3算法基于该方法, 实现了对STR和STR2算法的优化[6], 但STR3算法不能直接运用到负表中, 当约束中支持元组过于庞大时, 其处理元组依然很多. 因此, 受STR3算法的启发, 本文提出了一种负表约束算法STRN3, 对STR-N算法进行优化.

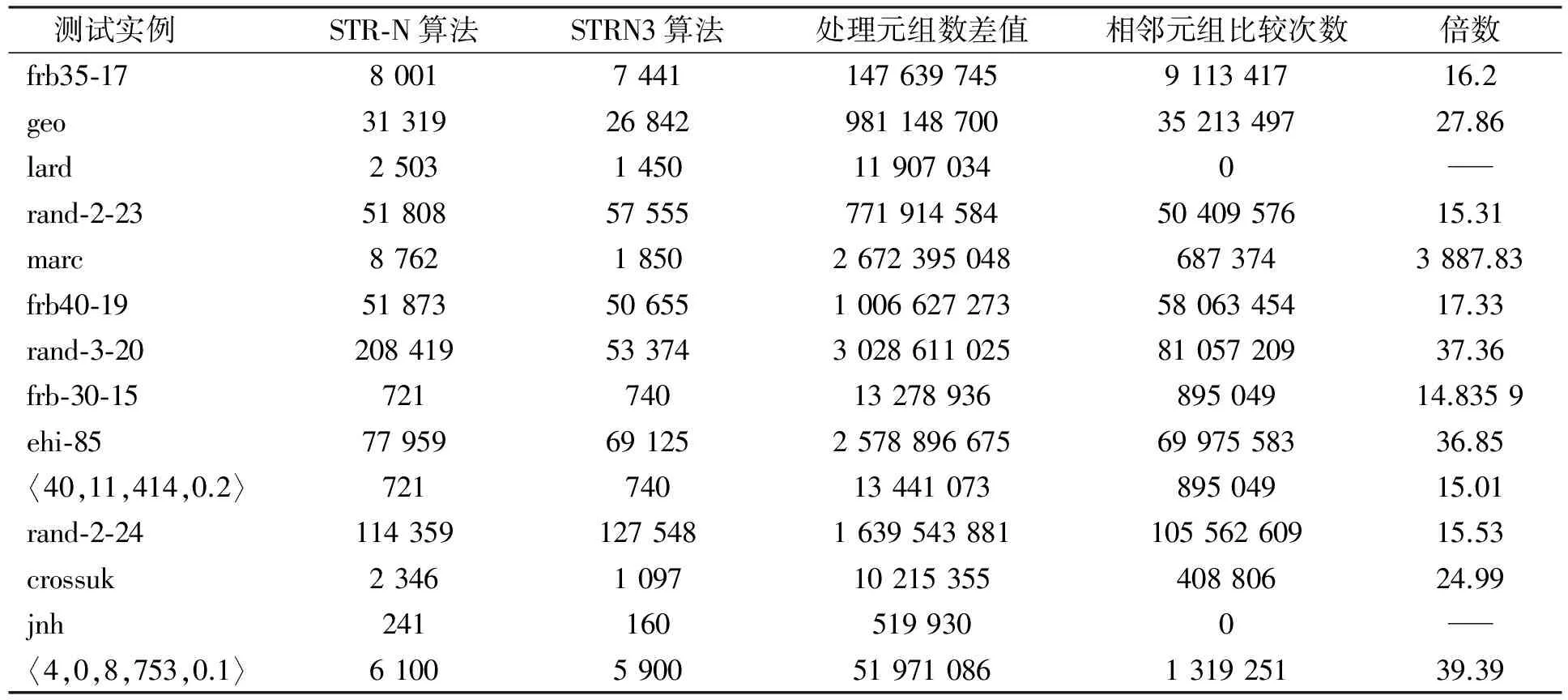
在STRN3算法中, 如何准确、 高效、 快速地寻找值支持的方式成为其最大的难点, 在直接对负表约束进行处理的算法STR-N中, 当判断某个值是否存在支持时, 必须将全部有效元组均遍历一遍, 该方法遍历元组数量过多[7], 且由于其为负表约束, 也不能同正表约束直接在有效的正表元组中找到支持的元组. 对于STRN3算法, 其将负表分解为每个变量值的升序子表table(C.X.a), 检索操作在子表中进行, 当判断某个值是否存在支持时, 不用再遍历所有有效元组, 而是在上次约束传播的基础上, 继续寻找该值的最小支持区间即可, 对于上次约束传播前已经遍历过的元组, 变为当前无关元组, 不会再在该次及以后的约束传播中被访问, 因此减少了时间复杂度. 实验结果表明, 在特定结构实例中, STRN3算法相对于STR-N算法和STR3算法, 优势明显, 特别是在一些结构突出的实例中, 效率甚至提升4～5倍.

1 预备知识

定义1(约束网络)[8]一个约束网络P通常由一个三元组构成, 表示为P=(X,D,C), 其中:X={X1,X2,…}是一个有限的变量集合;D={a1,a2,…,ad}是变量的有限值域集合;C={C1,C2,…}是一个有限约束集合.

定义2(弧相容)[9]给定一个约束C, 对于任意一个变量X∈scp(C)中的任意一个有效值a, 称约束C是有支持的, 当且仅当存在至少一个元组t∈C, 使得a=t[X], 且对于任意一个不同于变量X的变量Y, 其中Y∈scp(C), 使得t[Y]为变量Y的当前有效值. 如果对每个X∈scp(C), 每个值a∈dom(X)在C中至少存在一个支持, 则称约束C是弧相容的.

定义3(稀疏集) 稀疏集是一个抽象的数据结构, 用S表示, 其由三部分组成, 分别为两个整型数组dense,sparse和一个整型变量members. dense表示数组的常规表示形式, sparse表示dense中索引与数值对调后的数组, members表示dense中有效值的最大索引值.

例1dense,sparse,members列于表1, 其中： 值2,0,3有效; 1,5,4无效. 由于值0存放在数组dense中索引值为1的位置, 则sparse[0]=1.

表1 稀疏集示例

2 STRN3算法设计

2.1 定 义

定义4(table_all(C,X,a)) 将约束C的变量X值a的有效正子表与负子表进行合并, 并进行升序排列, 记作table_all(C,X,a).

定义5(相邻元组) 设负表table(C,X,a)中的两个元组t1与t2, 其在table_all(C,X,a)中相邻, 则t1与t2称为相邻元组.

例2图1为(C,X,0)的负表约束元组和全部元组. 由图1可见, 负表table(C,X,a)中的元组t1： {0,0,0}和t2： {1,0,1}, 在table_all中相邻, 则t1与t2为相邻元组.

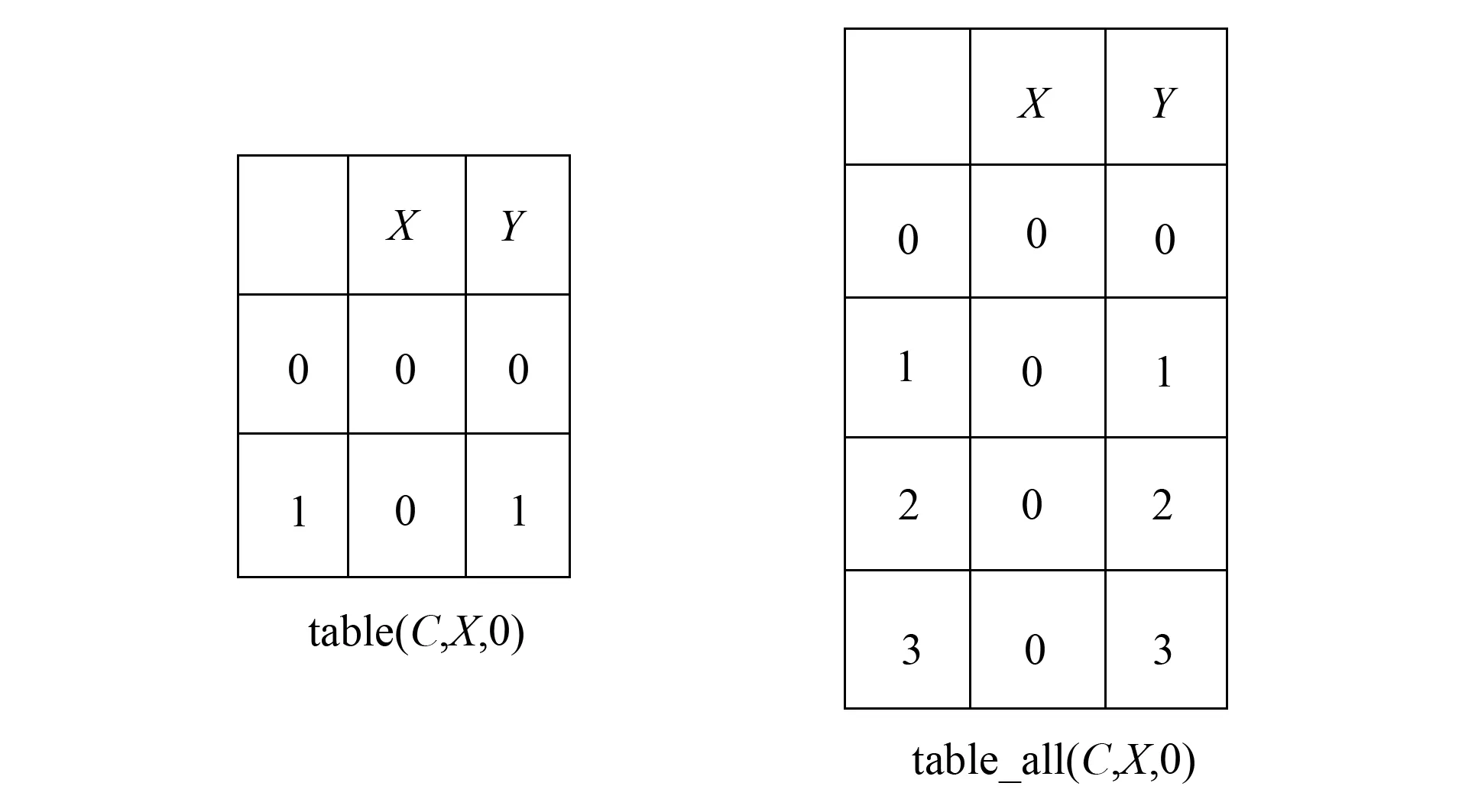
图1 (C,X,0)的负表约束元组和全部元组Fig.1 Negative table constraint tuples and all tuples of (C,X,0)

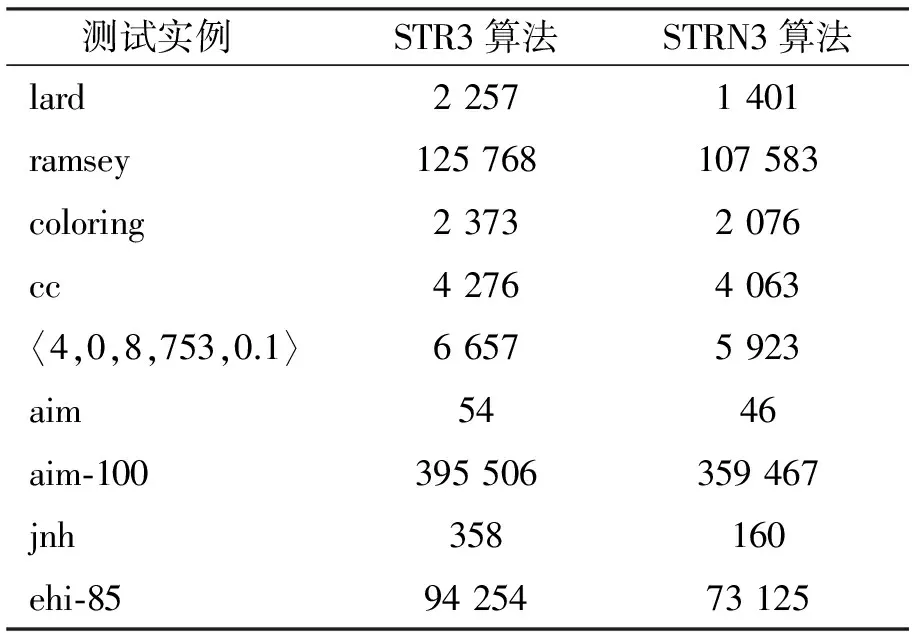
定义6(有效支持区间) 设负表table(C,X,a)已升序排列, 并存在两个元组t1与t2, 且t1

例3假设在图1的实例中, 所有元组均有效, 则大于table(C,X,0)[1]={0,1}存在有效支持元组(0,2)和(0,3), 且包含现在的最小支持元组(0,2), 故为最小有效支持区间.

2.2 算法思想

本文基于STR3算法, 将其思想应用于负表约束, 提出STRN3算法. 该算法实现了对STR-N算法的改进, 相比于STR3算法, STRN3算法可直接在负表中进行处理, 并舍弃了数据结构----dep(C,k), 使得对该结构的维持时间减少到0, 该算法也由路径最优算法转变成近似路径最优算法[9]. STRN3算法的核心思想如下： 将负表约束按变量值的形式划分为子表table(C,X,a), 对每个子表进行升序排列, 并对每个子表进行递归处理, 对于判断变量值是否存在支持时, 不再遍历整个负表, 而是在上一次每个子表的最小支持区间处, 继续在排序完全的子表中, 向升序方向继续遍历并判断是否存在支持. 对于每个子表的最小支持区间, 共有4种处理情况, 需按照各自情形进行后续判断和处理.

1) 上次传播最小支持区间为(-1,p). 从该子表索引p处(table(C,X,a)[p]), 向升序方向寻找有效元组, 设第一个有效元组为索引p1处的元组t1, 将该元组与当前最小有效元组进行比较, 若不相等, 则找到最小支持区间, 区间为(-1,p1); 若相等, 则未找到最小支持区间, 继续向升序方向寻找下一个有效元组, 设该元组为索引p2处的元组t2, 判断t2与t1是否为相邻元组, 若不等, 则找到最小支持区间, 区间为(p1,p2)； 若相等, 则继续寻找, 直到找到索引pn处的有效元组tn, 且与上一有效元组不为相邻元组, 此时最小支持区间为(pn-1,pn).

2) 上次传播最小支持区间为(p1,p2). 从子表索引p2处, 向升序方向寻找有效元组, 设第一个有效元组为索引p3处的元组t3, 判断t1与t3是否为相邻元组, 若不等, 则找到最小支持区间(p1,p3)； 若相等, 则与1)中相等后的处理逻辑一致, 直至找到最小支持区间(pn-1,pn).

3) 上次传播最小支持区间为(p,-1). 判断索引p处的元组t是否小于当前最大有效元组, 若小于, 则在元组t与最大有效元组中必存在有效支持元组, 本次最小支持区间仍为(p,-1); 若不小于, 则不存在有效元组, 则该值不再存在支持, 约束传播失败, 将该值删除.

4) 上次传播最小支持区间为(-1,-1). 此时该变量值负子表中的全部不支持元组均无效, 若该值仍然是该变量的有效值, 则必存在有效支持.

以上4种情形均为向升序方向寻找到有效元组的情形, 若最终找不到有效元组, 则按以下两种情形处理：

1) 上次传播最小支持区间为(-1,p)(p≠-1). 若按上述寻找最小支持区间对应方法中未找到有效元组, 则此时负表table(C,X,a)中不存在有效元组, 即值a不存在有效的冲突元组, 若此时值a在变量X中仍为有效值, 则必存在支持, 此时最小支持区间为(-1,-1).

2) 上次传播最小支持区间为(n,m)(n≥0,m>n). 若按上述寻找最小支持区间对应方法中, 未找到有效元组, 则在小于table(C,X,a)[n]的元组中, 不存在有效元组, 将元组table(C,X,a)[n]与当前最大有效元组相比较, 若小于, 则大于table(C,X,a)[n]的元组中, 必存在有效支持元组, 此时最小支持区间为(n,-1); 若不小于, 则不存在有效支持元组, 约束传播失败.

STRN3算法为细粒度算法, 一旦变量X的值a在约束传播过程中被删除, 则调用STRN3算法, 而在预处理阶段, 是对所有初始值进行处理, 将此时不满足相容性的值删除, 因此该阶段不可能调用到STRN3算法, 则在预处理阶段中先采用非细粒度算法进行处理. 本文采用STR-N算法, 在应用该算法做出预处理操作后, 必存在值被删除情形, STRN3算法自然被调用.

3 实验结果与分析

为了证明STRN3算法的改进效果, 选取STR-N算法和STR3算法进行比较. 算法实验操作系统为32位的Win7操作系统, 硬件资源为Intel (R)Core(TM)i7-3770 CPU@ 3.40 GHz内核, 3.46 GB内存, 采用JAVA语言. 3种算法均采用dom/ddeg变量启发式和字典序值启发式[10]. 实验选取的测试实例均来自约束求解问题的标准测试实例网站(http:// www.cril.univ-artois.fr/～lecoutre/benchmarks.html), 3种算法的对比结果分别列于表2～表4. 其中： 运行各算法时间的单位均为ms, 将运行时间的上限设为600 000 ms, 当超出此时间后, 不再运行; 表2和表3中的运行时间均为运行时间平均值, 测试实例多数为10个, 但marc问题系列由于时间长度问题, 只测试了5个实例, crossuk问题系列由于负表约束过大, 元组存储超出内存限制, 仅进行2个实例的测试.

表2中, 处理元组数差值表示在STR-N算法中对元组的处理个数与在STRN3算法中对元组处理个数的差值, 相邻元组比较次数表示在STRN3算法中对于2个元组是否能成为相邻元组的判断次数, 倍数表示处理元组数差值与相邻元组比较次数之间的倍数, 当相邻元组比较次数为0时, 用符号“-”表示. STRN3算法的处理过程较STR-N算法复杂, 其需要对元组的大小进行比较, 对元组的有效性进行检查, 并判断元组是否相邻等, 其中判断元组是否相邻最耗费时间. 通过以上分析可知, 倍数能成为STRN3算法和STR-N算法的比较参数, 对于处理的元组数, 当STR-N算法比STRN3算法高出一定倍数时, STRN3算法通常会表现出更优秀的特质.

表2 STRN3算法与STR-N算法对比结果

由表2可见, 虽然处理元组数差值全部为正数, 即STRN3算法处理了更少的元组, 但却表现出部分STRN3算法更优, 部分STR-N算法更优, 原因是对于STR-N算法表现更优秀的实例, 在STRN3算法中, 相邻元组的比较次数过多, 耗费了时间, 使得少处理的元组数不足与相邻元组比较次数的时间相抵, 因此, 用时更多、 效率更低； 其他实例中, 或者是处理元组数差值较高, 在所处理的元组数上, STRN3算法明显小于STR-N算法； 或者在处理元组数量上虽没能大幅度减少, 但在相邻元组的比较次数上, STRN3算法的值很低, 甚至为零, 因此STRN3算法运行效率更高.

表3为STRN3算法与STR3算法的平均对比结果, 其中对于每个实例, 负表约束中的元组数均小于其转化为正表约束的元组数, 因此, STRN3算法比STR3算法处理元组数少, 效率更高. 表4为STRN3算法与STR-N算法最优对比结果. 表4中每行的问题实例不再是问题系列, 而是一个具体的实例, 且所有实例都是STRN3算法较STR-N算法更优, 优化效果约为5倍, 其中large-96-unsat_ext优化效果最高.

表3 STRN3算法与STR3算法对比结果

表4 STRN3算法与STR-N算法最优对比结果

综上所述, 本文基于STR3算法, 通过放弃遍历不相关元组的方法, 优化了STR-N算法, 提出了STRN3算法, 该算法的最大优点为快速地寻找值支持的方式, 并且STRN3算法放弃了STR3算法中的dep数据结构, 成为一种近似路径最优算法. 由实验结果可得如下结论：

1) 当实例中支持元组数多于不支持元组数时, STRN3算法相对STR3算法效率更高；

2) 对于实例中元组的处理数量, STR-N算法较STRN3算法高出一定差值时, STRN3算法相对STR-N算法效率更高；

3) 元组的处理数量为影响STRN3算法效率的第一因子, 此外, 相邻元组的检查次数也同样重要, 成为影响STRN3算法效率的另一个重要因素, 时间效率与检查次数成反比, 当处理元组数与相邻元组的检查次数比值达到一定值时, STRN3算法效率更高, 但无法得到边界明确值.

[1] Freuder E C, Mackworth A K. Constraint Satisfaction: An Emerging Paradigm [J]. Handbook of Constraint Programming, 2006, 2: 13-27.

[2] Mackworth A K. Consistency in Networks of Relations [J]. Artificial Intelligence, 1977, 8(1): 99-118.

[3] Lecoutre C, Szymanek R. Generalized Arc Consistency for Positive Table Constraints [C]//Proceedings of the 12th International Conference on Principles and Practice of Constraint Programming. Berlin: Springer, 2006: 284-298.

[4] Lecoutre C, Szymanek R. Generalized Arc Consistency for Positive Table Constraints [C]//Proceedings of the 12th International Conference on Principles and Practice of Constraint Programming. Berlin: Springer-Verlag, 2006: 284-298.

[5] Lecoutre C, Likitvivatanavong C, Yap R H C. STR3: A Path-Optimal Filtering Algorithm for Table Constraints [J]. Artificial Intelligence, 2015, 220: 1-27.

[6] Lecoutre C. STR2: Optimized Simple Tabular Reduction for Table Constraints [J]. Constraints, 2011, 16(4): 341-371.

[7] LI Hongbo, LIANG Yanchun, GUO Jinsong, et al. Making Simple Tabular Reductionworks on Negative Table Constraints [C]//Twenty-Seventh AAAI Conference on Artificial Intelligence. Washington, DC: AAAI Press, 2013: 1629-1630.

[8] Lecoutre C. Constraint Networks: Techniques and Algorithms [M]. Piscataway, NJ: IEEE Press, 2009.

[9] Lecoutre C, Likitvivatanavong C, Yap R H C. A Path-Optimal GAC Algorithm for Table Constraints [C]//Proceedings of the 20th European Conference on Artificial Intelligence. Amsterdam: IOS Press, 2012: 510-515.

[10] Boussemart F, Hemery F, Lecoutre C, et al. Boosting Systematic Search by Weighting Constraints [C]//Proceedings of the 16th European Conference on Artificial Intelligence. Amsterdam: IOS Press, 2004: 146-150.