温玉卓，唐胜达，邓国和

（广西师范大学a.经济管理学院；b.数学科学学院，广西桂林541004）

0 引言

定义MArP风险过程：

其中,u是初始盈余资金，常数c＞0是保费率。不妨设c=1，设J={}J(t),t≥0是不可约连续时间Markov过程(CTMC)，称J为环境过程。J的有限状态空间为EJ={1,2,…,M}，状态i∈EJ表示保险公司所处的风险环境。计数过程N(J(t))表示风险过程在(0,t]的索赔次数。设{(J(t),N(J(t))),t≥0}构成一Markov到达过程[1](Markov Arrival Process，MArP)。具体地，在状态空间EJ×N上存在两个M阶矩阵，满足：

①Q(0)+Q(1)构成环境过程J的转移率矩阵；

②对所有j,k∈EJ,j≠k,qjk(0)≥0表示环境状态由j转移至k时，没有索赔发生的转移速率；

③对所有j,k∈EJ,qjk(1)≥0表示环境状态由j转移至k时，发生索赔的转移速率。

在风险过程（1）中，Xi表示风险过程的第i次索赔大小。给定环境状态时，设索赔序列{Xi}相互独立。本文假定索赔Xi具有PH分布，由于PH分布对于一切具有正支撑分布类稠密[2]，因而这一假设使得索赔更具一般性及概括性。设索赔受环境过程J影响，即当环境状态由j转移至k并发生索赔时，险种索赔额的分布为PH(βk,Bk),记bk=-Bke，其中e是维数适当的单位列向量，不失一般性，对所有k∈EJ，设PH(βk,Bk)对应的潜在Markov过程的瞬间状态空间为Eph={1,2,…,K}。本文总是假定风险过程（1）满足正的安全负荷条件：

其中μk=-βkBk-1e表示在k状态发生索赔额的期望,{πj,j∈EJ}是环境过程J的平稳分布,即

本文主要讨论MArP风险过程（1）的与破产时间相关的性能指标。基于此，定义：

称τ为风险过程（1）的破产时刻。若对任意i∈Em1，都有V(t)＞0，则令u,0)。

定义破产时刻τ的分布函数为：定义破产时刻τ的Laplace-stieltjes变换(LST）：

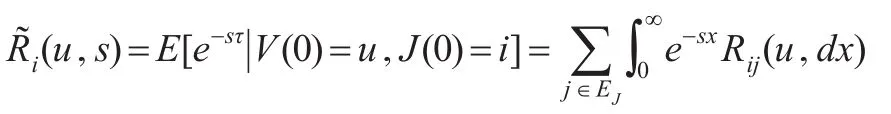
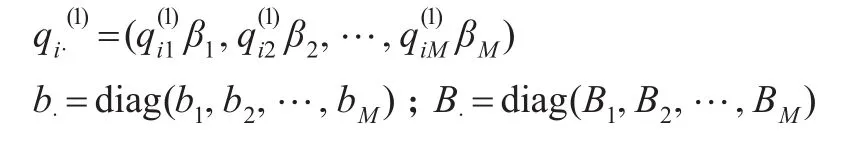
1 模型分析

Markov流体队列（MFQ）最初源于网络通讯,它在近二十年得到了迅速发展，已被成功应用于网络通讯、供应链、火灾防控、风险理论等领域。下面对本文需要用到的MFQ理论进行简单介绍。

1.1 MFQ的忙期

设{(Y,φ)}={(Y(t),φ(t)),t≥0}是二维随机过程，其中，过程φ是空间为E，转移率矩阵为T的CTMC，称φ={φ(t),t≥0}为背景过程，Y={Y(t),t≥0}称为水平过程，过程Y的变化满足如下等式：于是，称为Markov流体队列（MFQ）。

称ci,i∈EJ为纯输入率，本文设ci只取值正负两种情况，对状态空间分类E=E+∪E-，其中，E+={i∈E,ci＞0}，E-={i∈E,ci＜0},定义矩阵C+=diag{ci,i∈E+}，C-=diag{-ci,i∈E-}，C=diag(C+,C-)。对应于E=E+∪E-，转移率矩阵T可写成如下分块形式：

下面定义首达时（first passage time,FPT）：

其中，θ表示初始水平为u的随机流体队列首次回到初始水平u的时间。显然，θ与流体队列的初始水平无关。χ表示初始水平为u的随机流体队列首次达到水平0的时间。记θ与χ相应的分布函数为：

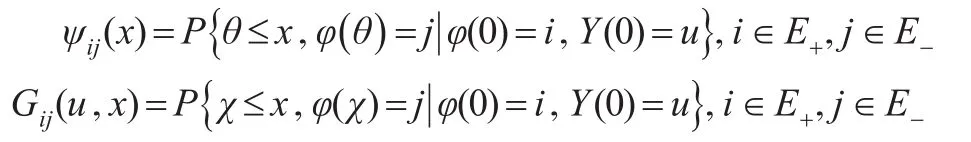
记矩阵ψ(x)=(ψij(x))，G+-(u,x)=(Gij(u,x))。记θ与χ相应的LST变换为：

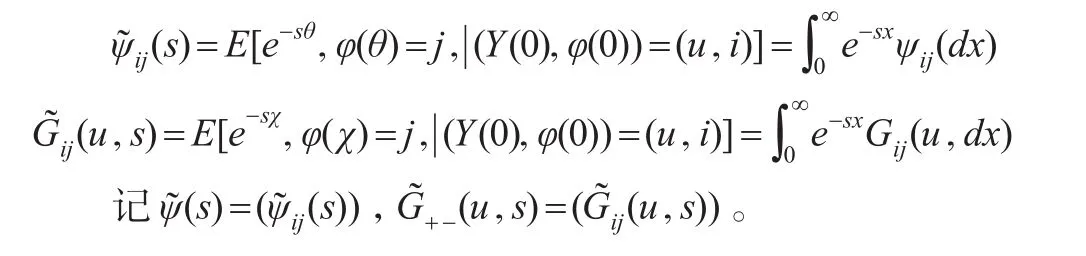
由文献[3],有如下引理成立：

引理1：对MFQ{}(Y,φ)有如下等式成立：

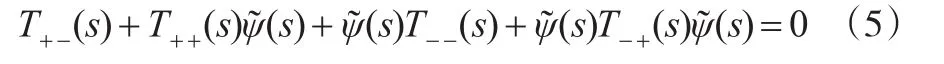
对于上Riccati方程，由L-R算法[3]可求解(s)。

1.2 模型转换

本文基于Asmussen[4]和张超权[5]等的方法，提出一种新的改进算法，称为Erlang逼近算法，不同于Asmussen[4]和张超权[5]将风险过程（1）转化与之具有相同演变规律的MFQ模型，本文中，风险过程（1）转化为初始水平为0的MFQ模型序列。使得MFQ模型序列逼近具有相同演变规律的MFQ模型，本文提出的这一改进算法的优点在于，Erlang逼近算法保持了原方法的优点，同时，这一算法的所有指标量的讨论都限定在一个忙期内,即求解过程中只涉及一个指标量(忙期)的计算,同时，Erlang逼近算法较之文献[5-8]，这一转换关系回避了MFQ模型的流体水平过程的各种演变情况的分类及讨论,使得计算程序十分简洁，而且算法概率意义直观，同时，对于Asmussen等的方法不可能讨论的量，如MFQ模型最值的分布等，也可以应用这一方法进行求解。下面将详细介绍这一方法。

图1 风险过程样本路径

图2 风险过程对应的MFQ模型样本路径

首先，如图1和图2所示，假定风险过程（1）在发生索赔时，并非一次性付清，而是以速率1连续支付，直至付清。于是风险过程（1）转化为MFQ模型(t)),t≥0},见图2。其中,环境过程(t)的状态空间为，记为过程的初始分布向量。类似于文献[3，6，9],根据背景过程的转移特点，得到相应的转移率矩阵，其中，构造如表1所示，表中的第一列表示初始状态i，第二列表示转移状态j，第三列表示对应的转移率，i≠j，转移率矩阵元素可以根据转移率矩阵行和为0这一性质得到。

表1 过程的转移率矩阵的元素结构

表1 过程的转移率矩阵的元素结构

初始状态i i(i,j,l)(i,j,l)i其他转移状态j 转移率j1j q(0)ij Bj(l,ν)bj(l)(i,j,l)其他q(1)ijβj(l)0备注i,j∈EJ，l,ν∈Eph，k=1,2,…,M.

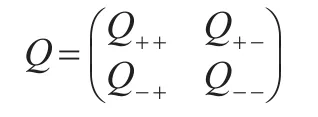
相应的转移率矩阵记为Q(n)，根据，将转移率矩阵Q(n)改写成如下分块矩阵形式：

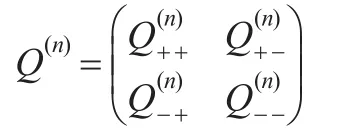
类似地，定义：

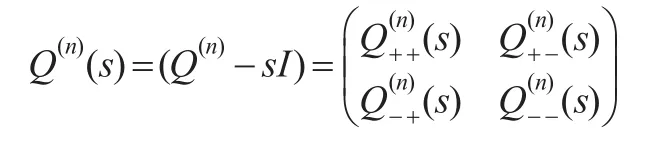
1.3 主要结果

基于MFQ序列{(V(n),J(n))}，对n=1,2,3,…，定义首达时序列：

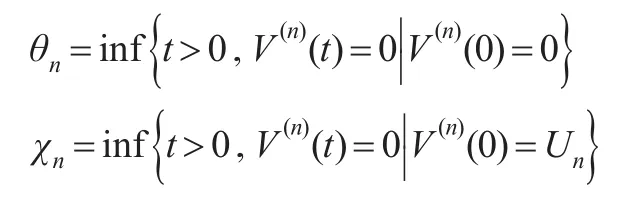
其中，θn表示{(V(n),J(n))}从初始水平为0首次回到初始水平0的时间。χn表示{(V(n),J(n))}从初始水平为Un首次达到水平0的时间。

类似地，定义θn与χn的LST变换矩阵，其中：

类似地，定义τn为MFQ{(V(n),J(n))}对应初值为Un的风险过程（1）的破产时刻，设τn的LST变换矩阵为

下面给出本文的主要定理及证明。

定理1：设给定初始盈余u及初始环境状态i∈EJ，则MArP风险过程（1）的破产时间的LST变换u,s)满足：

其中，符号A1·表示取矩阵A1·的第一行元素。有：

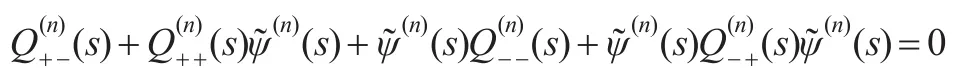
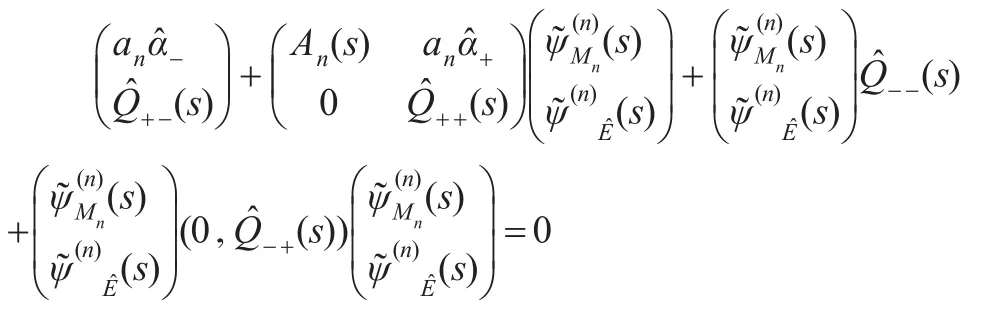
注意到初始环境状态给定为i∈EJ，于是=ei，=0,其中，ei表示第i个元素为1，其他元素为0的维数适当的行向量。从而取上式第一行，得：

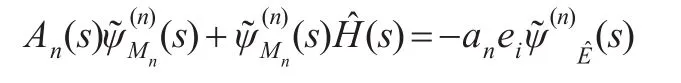
由文献[10],解得上式：

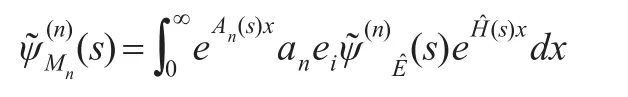
注意到An(s)=An-sI，于是有：

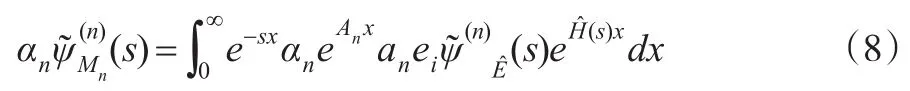
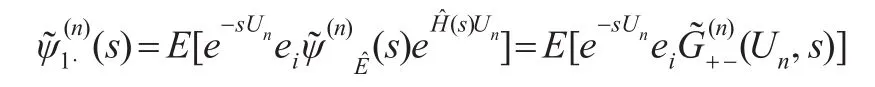
对应的仿文献[7]推导，如图3所示，在{(V(n),J(n))}中，有如下关系：

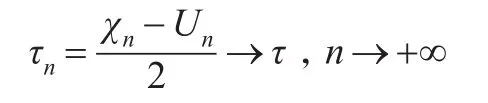
证明：由引理1,MFQ序列

图3 Un，τn与χn的数量关系

于是：

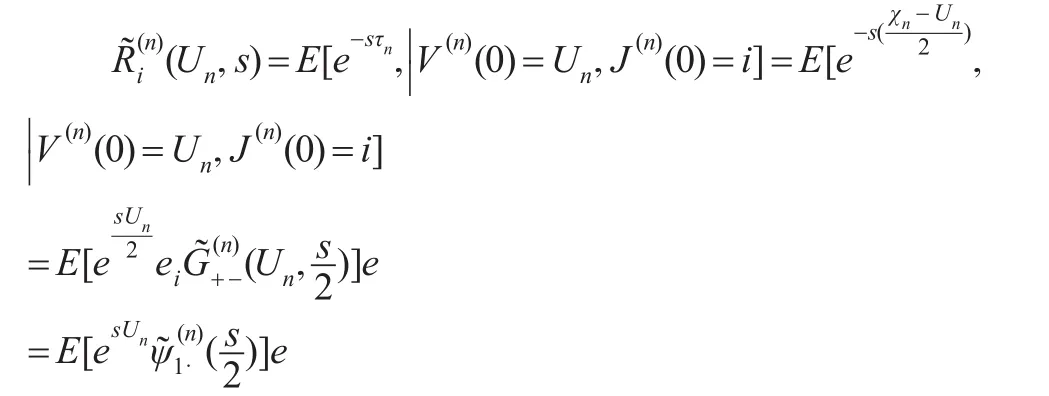
注意到，Un服从分布，故，当n→+∞时，随机变量Un收敛为常数u(注：本文的收敛均指以概率1收敛)[11],于是，令上式左右两边同时令n→+∞，得到：

定理显然。

②定理1给出了破产时间的LST变换的一个逼近算法,由文献[11,13]可知，即使当阶数n很小时,这一算法也具有优良的精度,文献[9]中给出了破产时间LST的不同证明方法。显然本文的证明方法更为简洁明了。

显然，令s=0，有如下推论成立：

推论1：设给定初始盈余u及初始环境状态i∈EJ，则MArP风险过程（1）的最终破产概率为：

同时，根据PH分布的性质，可以推得如下结论：

推论2：设给定初始盈余u及初始环境状态，则MArP风险过程（1）的破产赤字服从PH分布：

2 数值实例

为了说明本文的理论结果，下面给出一数值实例：考虑具有两个风险状态的MArP风险过程，设EJ={1,2}，其中1表示高风险状态，2表示低风险状态，背景过程对应于不发生索赔和发生索赔的转移率矩阵分别设为：当背景过程转移至状态1时，索赔服从分布PH(α,A)，其中，α=(1,0)，A=，背景过程转移至状态2时，索赔服从分布PH(β,B)，其中设过程的初始盈余为u=1，于是，由定理1可以得到两状态下风险过程（1）对应的破产时间的LST变换函数，对LST变换函数取逆变换[12]，于是得到两风险状态下破产时间的概率密度函数值如表2所示，从表中数据可见，本文提出的这种逼近新算法，借助了Erlang逼近速度快这一优点，不需计算任何中间量即可求得所需的性能指标。

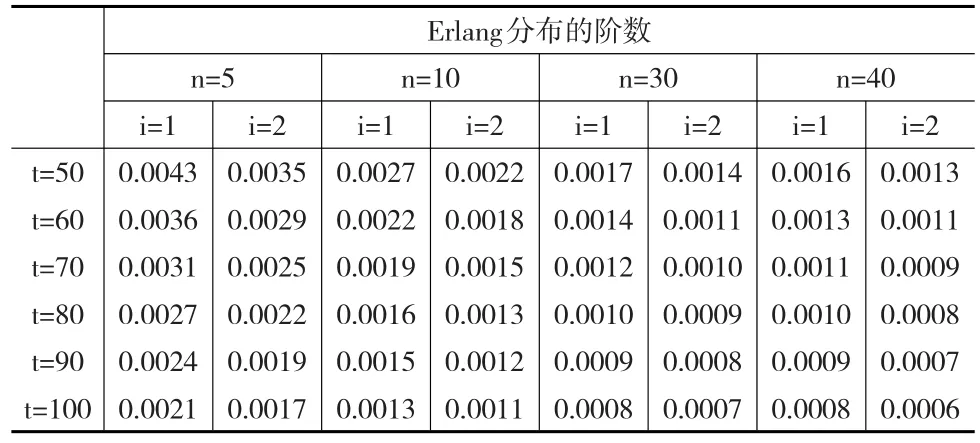
表2 两风险状态下破产时间的概率密度函数值

同时，根据本文推论1的结论，可以计算出在不同Erlang分布阶数下风险状态1和2的终破产概率，如图4所示，从图中可见，Erlang逼近的精度是可以满足一般风险度量需求的[11]。

3 结论

本文分析了在随机环境下的风险过程，即一类由Markov随机环境过程同时影响风险过程的索赔大小及频率，在索赔服从PH分布情形下，将这一风险过程转化为MFQ模型，在转换过程中，本文改进了Asmussen等转换方法，即将风险过程转化为一个初始水平为0的MFQ序列，这一转换关系将对风险过程性能指标的讨论限定在一个忙期内,从而使得问题求解的计算简洁直观，应用MFQ理论探讨了这一风险过程的破产时间分布的LST变换的表示式，给出了最终破产概率以及破产赤字分布。本文的结论具有实际可操作性，这些结论对于保险公司分析外界随机环境因素对保险业务的经营及管理的影响提供了理论基础，对保险人规避风险，稳健经营具有重要的指导意义。

[1]Latouche G,Ramaswami V.Introduction to Matrix Analytic Methods in Stochastic Modeling[J].Technometrics,2012,43(3).

[2]Asmussen,Koole G.Marked Point Processes as Limits of Markovian Arrival Streams[J].Journal of Applied Probability,1993,l30(2).

[3]Ahn S，Ramaswami V.Efficient Algorithms for Transient Analysis of Stochastic Fluid Flow Models[J].Appl.Probab.,2005,42(2).

[4]Asmussen S.Stationary Distributions via First Passage Times[J].In Advances in Queueing:Theory,Methods,and Open Problems,1995.

[5]张超权,刘晓辉.求解MArP风险过程破产时间的新方法[J].统计与决策,2015,（21）.

[6]Badescu A L,Breuer L，et al.Risk Processes Analyzed as Fluid Queues[J].Scand.Actuar,2005,(15).

[7]Badescu A L，David L.Applications of Fluid Flow Matrix Analytic Methods in Ruin Theory-A Review[J].Rev.R.Acad.Cerie A.Mat.2009,103(2).

[8]Ramaswami V.Passage Times in Fluid Models With Application to Risk Processes[J].Methodol.Comput.Appl.Probab.,2006,8(4).

[9]Tang S,Tan L.Erlangian Approximation to Finite Time Probability of Blocking Time of Multi-class OBS Nodes[J].Photonic Network Communications,2015,30(2).

[10]Bhatia R,Rosenthal P.How and Why to Solve the Operator Equation AX-XB=Y[J].Bull Lond Math Soc,1997,(29).

[11]Asmussen S,Avram F,Usabel M.Erlangian Approximations for Finite Time Ruin Probabilities[J].N Bulletin,2002,(32).

[12]Jagerman D L.An Inversion Technique for the Laplace Transform[J].Bell System Technical Journal,1982,61(8).

[13]Ramaswami V,Woolford D，Stanford D.The Erlangization Method for Markovian Fluid Flows[J].Annals of Operations Research,2008,(160).