基于凸优化和切比雪夫伪谱法的再入轨迹优化
2018-02-26陈嘉澍
陈嘉澍


摘要
高超声速飞行器再入轨迹优化问题,即在规定的飞行任务下,寻找一条某种性能指标最优,又不违背热流,动压,过载,禁飞区等各种约束的飞行轨迹。面对再入轨迹优化问题的强非线性,多约束。本文通过线性化和Chebyshev伪谱法离散化,以及对非凸约束进行凸化处理,将非线性优化问题转化为二阶锥规划(Second Order ConicProgramming,SOCP)问题,然后采用凸优化方法快速求解。数值仿真表明该方法能快速高效地求解多约束条件下的再入轨迹优化问题,并且在优化的过程中以及终端状态均满足所给的约束。
【关键词】再入制导 切比雪夫伪谱法 凸优化
1 引言
轨迹设计是概念设计中的关键步骤,目的是使飞行器的性能与其所执行的飞行任务相匹配。所谓轨迹优化,是指在规定的飞行任务条件下,寻找一条某种性能指标最优,而又不违背热流,动压,过载等各种约束的飞行轨迹。高超声速飞行器的飞行轨迹优化对其设计有着十分重要的意义。
高超声速飞行器由于飞行空域和速度大范围变化,具有很强的非线性动力学特征,面临更复杂的运动方程组。在大气层内长时间高超声速机动飞行,导致飞行器自身的热力学环境十分恶劣,为了保证满足飞行器的热防护系统,弹载设备以及机身结构正常工作,再入轨迹需要满足热流率,动压以及过载等物理量的不等式约束。在实际运行中,导航系统的正常工作需求,领空限制问题等,要求再入轨迹满足航路点等式约束以及禁飞区不等式约束。
近年来,凸优化理论及方法取得较大发展并被广泛应用。随着凸优化方法的完善和计算机技术的发展,大规模凸优化问题己能够在有限时间内获得最优解。随后采用凸优化方法求解飞行器轨迹优化的研究逐渐增多,如行星软着陆问题。Liu和Lu近年来针对轨迹规划的凸优化建模与方法展开了深入研究。在文献[7]中,Liu采用凸优化方法研究了在为了避免碰撞以及非线性末端约束等复杂约束条件情况下的航天器轨迹优化问题。文献[8]基于二阶锥规划,并且使用序列线性化和松弛技术,而后将线性化的运动方程组离散化,完成了飞行器的再入轨迹优化;在此基础上。文献[9]实现了最大化侧向角航程的再入轨迹优化。国内的谭峰[10]将凸优化方法应用于高超声速飞行器轨迹跟踪控制,并在此基础上进行在线制导与轨迹优化。林晓辉等人基于凸优化理论研究了月球定点着陆的轨迹优化[11],陈洪普将凸优化方法应用于高超声速飞行器的再入制导过程当中,并且应用了模型预测控制的方法[12]。
本文考虑具有非线性运动方程的高超声速飞行器轨迹规划问题,建立再入阶段轨迹规划的非凸最优控制模型。在此基础上,利用线性化,离散化,和凸化的处理,将非线性动态约束转化为凸约束。同时,由于Chebyshev伪谱法在求解轨迹优化问题时具有较快的收敛性和较高的精度[13],因此在离散化的过程当中,采用Chebyshev插值法对运动方程组进行离散化。最后在此基础上,利用序列凸优化算法进行迭代求解获得再入最优轨迹。通过数值优化结果,验证了该方法的有效性,准确性和计算效率。
2 基于凸优化的问题建模
2.1 再入运动模型
飞行器的再入段具有一定的特征,返回过程受力情况有一定特点。在高超声速飞行器再入过程中,发动机会被关闭,所以就没有推力和控制力的作用,这样只有万有引力和空气动力两种作用力对飞行器再入过程造成影响。因此,质心动力学方程中只考虑空气动力和万有引力的影响。
因此,简化的质心动力学方程为:则得下列运动方程:
其中λ,Φ是水平位置,r是高超声速飞行器质心相对于地心的高度,V是飞行器的速度,γ是弹道倾角,φ是航向角,m是飞行器的质量,α是攻角,σ是速度倾角。其中R0是地球的半径,h是飞行器质心到地球表面的距离。
阻力D和升力L的计算表达式为:
其中S是再入飞行器翼面的参考面积,CD,CL为阻力,升力系数。ρ为大气层空气密度,采用一般的指數形式为:
其中,ρ0是海平面处的大气密度,β为常数。
令(1)中状态向量为x=[λ,Φ,r,V,γ,φ]T,控制量为u=[α,σ]T,则(1)可变换为:
x=f(x,u,t)(5)
2.2 约束条件
再入过程中为保证飞行任务的顺利完成以及飞行器的的安全,应满足以下等式约束和不等式约束。
2.2.1 等式约束
终端约束为飞行器到达既定目标点的能量约束,具体包括高度,速度约束,表达式如下:
其中h=r-R0为飞行器与地球表面距离。此外,为了满足飞行任务需求与制导精度,终端约束应包括经纬度约束:
所以确定了飞行器起点位置和目标位置,总结为如下等式约束:
2.2.2 不等式约束
不等式约束一般包括热流,动压,过载三个约束条件,分别为:
其中Qmax(W/m2)是热防护系统允许的最大热流率,KQ是常数。
其中,Nmax是允许的最大过载。
大气密度函数中,为方便后续处理,令无量纲高度为h=(R-R0)/R0,则重新定义空气密度系数为:对(9)-(11)进行归一化处理得其中,
根据禁飞区可以用其中心位置和其相应的半径RiNFZ可得出禁飞区对飞行器轨迹的约束如下:
对于两个控制量倾侧角σ和攻角α也有相应的要求和约束:倾侧角一般限制在给定的区间(如[-π/3,π/3])以保证飞行稳定性;对于攻角α,对攻角的大小一定的约束要求即αmin≤α≤αmax,因此有如下关于控制变量的约束:
2.3 优化问题总结
根据上述运动模型和约束条件,然后再以时间最优为指标,再入轨迹优化问题可以描述为:
3 轨迹优化算法原理
3.1 问题描述的改进
由于最优控制问题P0的终端时间自由不利于后续的离散化处理。为了解决这个问题,本文引入终端时间tf作为新的控制量,并且归一化时间从而解决时间自由问题。
考虑到Chebshev伪谱法配点区间为τ∈[-1,1],因此按照一般对时间自由问题的处理方法,将时间由[0,tf]映射至[-1,1]区间,即令τ=2t/tf-1∈[-1,1],并将状态扩展一维至x=[xT,t]∈R7,同时将终端时间tf作为新的控制变量,而新的等价性能指标变为J=t(1)。
此外,本文采用己有的气动系数模型,将空气动力系数CL,CD看做是攻角α和速度V的函数,采用文献[15]数据拟合的结果,采用双变量气动系数模型,所以对于升力系数CL和阻力系数CD以及约束内的一些其他参数重新写出如下:
其中CL1,CL2,CL3,CD1,CD2,CD3,均为给定的常数。相应地,控制约束可以得出为:状态量约束:
至此,问题P0己等价转化为下面给出的P1:
其中,(·)'=d/dτ,τ∈[0,1]。问题P1中的性能指标函数J=t(1),表示为在终端时刻tf扩展状态的大小。显然,这样便将问题P0中的Lagrange项转化为Mayer,使其成为一个线性函数。从而使得P1中满足本文对SOCP求解方法中对于性能指标函数为凸函数的要求,且P1的解与原问题P0的解等价。
3.2 线性化
要进行序列凸优化处理,必须对PI中的动态方程进行线性化处理。令第k次迭代获得的基准轨迹为于是在第(k+1)迭代中,该非线性方程可以用下式近似逼近:
其中雅可比矩阵定义为,由于篇幅有限,具体表达式未列出。此外,余项的表达式为:
式中A,B,C依赖于基准轨迹X,而不依赖于当前轨迹的状态量和控制量,在计算时可以认为其是常数,从而实现了运动方程的线性化。
为保证线性化的有效性,则必须考虑可信域的问题,即:
其中ε∈R10为预先指定的常数向量。该式包含10个不等式,所以状态量和控制量的每一项都应满足上述不等式,即:
3.3 凸化处理
问题P1中路径约束(25)都是非凸的,我们必须对这些约束进行凸化处理才能使用凸优化方法求解问题。
路径约束(25)中的每一个非凸约束(不等式)均可表示为如下一般形式的不等式:
m为路径约束的个数,对于此类非凸约束,可以将约束沿前次优化所得轨迹Xk(即对应离散点处进行线性化,采用一阶逼近形式,获得近似的线性不等式约束:
其中是gp在Xk处的梯度。显然,由(25)所定义的可信域是保证线性化不等式约束(27)合理逼近原不等式约束(26)的必要前提条件。
3.4 用Chebyshev插值法进行离散化
要求解优化问题P1,在线性化运动方程(27)的基础上,对运动方程进行离散化。
要求解问题P1,需对线性化动态方程(25)在τ∈[0,1]上进行离散化,将微分方程约束转化为代数约束。首先,将问题的时间区间I=[τ0,τf]划分为M个子区间Im(m=1,…,M)。
由于Chebyshev伪谱法的配点都分布在区间[-1,1]上,因此,在每个子区间内,需将求解问题的时间区间Im(m=1,…,M)转化到区间[-1,1]上,对时间变量τ(m)做变换:
在Chebyshev伪谱法中,插值点的选取为
tk=cos((N-k)π/N),k=0,…,N(31)
由式(32)可知,t∈[-1,1],且它是N次Chebyshev多项式TN(t)的極值。第j次Chebyshev多项式为:
文献[16]证明了在CGL点处求得的近似解是最接近所求问题最优解的,且文中给出了误差表达式。为离散状态变量和控制变量,给出下列多项式:式中,Φj(t)是N次拉格朗日插值基函数为:
其中
由插值基函数的性质有
从而有
对状态向量和控制向量进行离散化之后,则可以得到离散时间系统运动方程为:
其中I是与Aik维数相同的单位阵。经过上述线性化和离散化之后最优化问题P,可转化为最优化问题P2并进行求解。
P2:mint(1)(35)
其中,t∈[-1,1],p=1,..,m,k=1,2,...。由文献[17]可得,经过处理和优化后的问题P:与原问题P1的解是相同的。
3.5 序列凸优化
序列凸优化是一种利用凸优化求解非凸优化问题的方法,即通过迭代求解一系列非凸优化的凸近似子问题,得到原问题的解。
在优化过程中,第一次迭代的初始轨迹为猜测的初值,后续迭代的轨迹的初值Xik为前一次迭代轨迹的求解结果x尸,即
式中k描述了序列凸优化中第k次迭代的相关参数,xik为第k次序列迭代的求解结果。
另外,为保证运动方程线性化的有效性和序列迭代的收敛性,在序列算法中应该增加相应的信赖域:
其中,Lq为第q次迭代对应的信赖半径。
所以求解问题P2的具体流程步骤如下所不:
步骤1令k=0,选择控制量的初始输入值(如α=35,σ=0),则可以得到初始的控制剖面ui0。在此控制输入量的情况下,对飞行器的运动方程组(1)进行积分,从而得到了初始的状态轨迹xik,并且将其作为序列凸优化算法第一次迭代求解的轨迹;
步骤2在第(k+1)次迭代中,利用第k次迭代获得的轨迹{xk,uk}建立SOCP问题P2。同时根据式(13),(14)对热流,动压,过载和禁飞区等约束的违反情况进行检查,如果出现违反约束的情况,则在问题P2中施加式(38)中相应的凸化约束。之后利用SOCP算法求解得到最优解:
步骤3检查是否满足收敛条件。若收敛条件(42)满足,则转至“步骤4”,否则,令Xik=Xik+1,k=k+1,并且跳转至“步骤2”。
步骤4优化问题P0解为Xik+1,迭代停止。
4 结果分析(43)
本文以CAV再入模型为例并MATLAB环境中进行数值优化和仿真试验以验证上述方法的有效性。
仿真实验在Windows 7中的MATLAB2014a环境下进行,硬件环境Intel Core i5-45903.30GHz处理器和4GB内存的PC机。SOCP问题采用轻量级凸优化求解算法包ECOS[18]求解,采用Yalmip建模工具箱[19]进行优化问题建模。
表1给出了CAA再入飞行器的任务描述,给出了相应的任务起点和目标点的水平位置和高度;并且给出了禁飞区的中心和半径。CAV飞行器的任务如表1。
已知的各个参数值和路径约束如表2所示。
设定的边界条件如表3所示。
关于控制量,倾侧角限制为σmax=π。式(40)中的可信域设置为
对于系统的离散化则设定参数N=300。
为了验证所提出的凸优化问题模型以及序列凸优化算法,针对CAV飞行器的再入轨迹进行了仿真计算。
仿真结果见图1~5。图2为CAV飞行器的地面航迹图,可以看出飞行器沿最优轨迹从初始位置到达目标位置,并且中间避过了两个禁飞区。而且由初始轨迹的误差之大可知,序列凸优化算法对初值不敏感的优点。
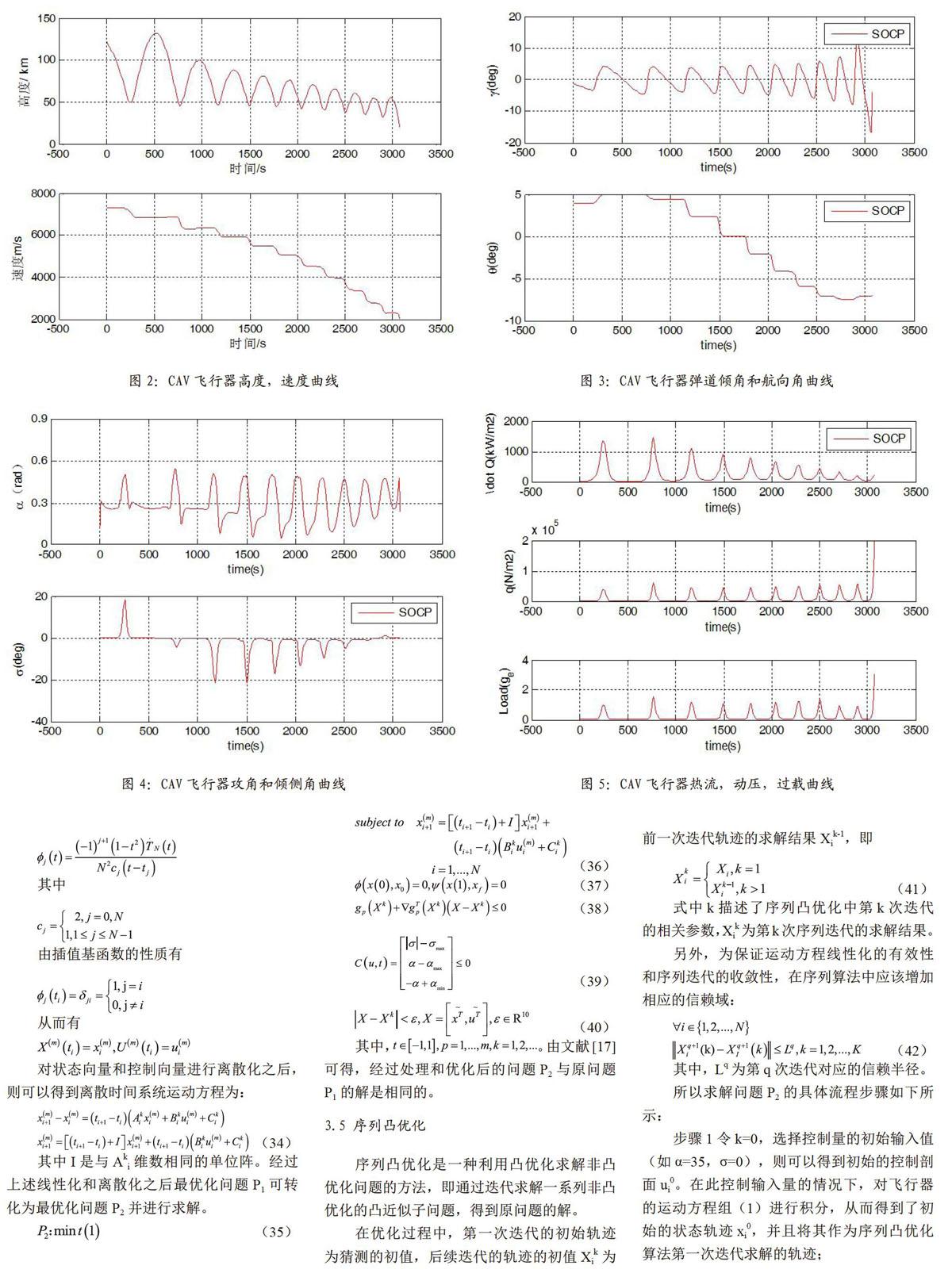
图2为轨迹优化过程中两个状态变量高度和速度随时间变化曲线,可以看出在给定的初始条件h0=122km,v0=7315.2m/s的情况下,经过优化处理最终两个状态量都满足终端约束hf=20km,vf=2000m/s。
图3为弹道倾角和航向角的曲线变化趋势和幅度,由图可知在给定的弹道倾角的初始约束γ0=-1.5°的情况下,最终经过优化之后的弹道倾角满足终端约束γf=-4°。而航向角变化幅度较小,可以保证CAV飞行器的轨迹符合所给初的约束。
图4是两个控制量攻角α和倾侧角σ随时间变化曲线,由图可知整个过程均满足控制变量约束条件。
图5为CAV飞行过程中动压,热流,过载随时间变化曲线,虽然动压和过载最后阶段变化较大,但是没有超过给定的最大值,满足约束。
由图2、3、4所得的表4可更加直观分析所得结果。
由图5所得的表5也可以直观的分析优化过程中的路径约束问题。
所以由上述两表可以更加直观地得出化后的轨迹满足先前给定的各个约束。
5 结论
本文基于凸优化理论和方法,对高超声速飞行器再入轨迹优化问题进行了建模和凸优化问题标准形式的表述。针对制约凸优化方法应用于再入轨迹优化的非线性状态方程,本文通过引入归一化时间,结合轨迹线性化和Chebyshev插值法對线性化方程的离散化以及无损凸化处理技术,将原问题转化为标准的SOCP问题。最后利用序列凸优化算法将其在MATLAB程序上实现,并且最后的仿真结果证明了上述方法的有效性。其能有效的求解高超声速飞行器轨迹优化问题,而且满足所提出的各项约束要求。
参考文献
[1]P.Lu,"Entry Guidance:A UnifiedMethod,"[J].Journal of GuidanceControl and Dynamics,vol.37,pp.713-729,2014.
[2]T.R.Jorris and R.G.Cobb,"Three-DimensionalTrajectory OptimizationSatisfying Waypoint and No-FlyZone Constraints,"[J].Journal ofGuidance,Control,and Dynamics,vol.32,pp.551-572,2009.
[3]Yan H,Wu H Y.Initial Adjoint-VariableGuess Technique and Its Applicationin Optimal Orbital Transfer[J].Journal of Guidance,Control,andDynamics1999,22(03):490-492.
[4]Enright P J,Conway B A.OptimalFinitethrust SpacecraftTrajectories Using CollocationandNonlinear Programming[J].Journal of Guidance,Control,andDynamics,1991,14(05):981-985.
[5]BOYD S,VANDENBERGHE L.Convexoptimization[M].New York:CambridgeUniversity Press,2004,1-15.
[6]ACIKMESE B,CARSON J M,BLACKMOREL.Lossless convexification ofnonconvex control bound and pointingconstraints in thesoftlandingoptimal controlproblem[J].IEEETransactions on Control Systems Techno logy,2013,21(06):2104-2113.
[7]LIU X.Autonomous trajectory planningby convex optimization[D].Iowa:IowaState University,2013.
[8]LIU X F,SHEN Z I,LU P,Entrytrajectory optimization by second-order cone program-ming[J].Journal of Guidance,Control,andDynamics,2016,39(02):227-241.
[9]LIU X F,SHEN Z J,LU P.Solvingthe maximum-cross-range problemvia successive second-order coneprogramming with a line search[J].Aerospace Science and Techn-ology,2015,47:10-20.
[10]譚峰,陈洪普,侯明哲等.高超声速再入飞行器基于凸优化的模型预测轨迹跟踪控[C].第32届中国控制会议.西安:中国自动化学会,2013:4167-4171.
[11]林晓辉,于文进.基于凸优化理论的含约束月球定点着陆轨道优化[J].宇航学报,2013,34(07):901-908.
[12]陈洪普.基于凸优化的模型预测控制在飞行器再入制导中的应用[D].哈尔滨:哈尔滨工业大学,2013.
[13]王立峰.Chebyshev局部配点法在轨迹优化中的应用[A].哈尔滨工业大学学报,2012,45(05):95-100.
[14]X.Liu,et al.,"Entry TrajectoryOptimizationby Second-Order ConeProgramming,"[J].Journal of GuidanceControl and Dynamics(Articles inadvance),pp.1-13,2015.
[15]孙勇.基于改进Gauss伪谱法的高超声速飞行器轨迹优化与制导[D].哈尔滨业大学博士学位论文,2012:20-37.
[16]ELNAGAR G,KAZEMI M A,RAZZAGHIM.The pseudospectrallegendre methodfor discretizing optimalcontrolproblems[J].IEEE Transactions on AntomaticControl,1995,40(10):1793-1796.
[17]X.Liu,et al.,"Entry TrajectoryOptimization by Second-Order ConeProgramming,"[J].Journal of GuidanceControl and Dynamics(Articles inadvance),pp.1-13,2015.
[18]Domahidi,et al.,"ECOS:AnSOCPSolverfor Embedded Systems,"[J].EuropeanControl Conference,Zurich,Switzerland,2013.
[19]J.Lofberg,"YALMIP:A Toolbox forModeling and Optimization inMATLAB2004.,"[J].Proceedings of theCACSD Conference,Taipei,Taiwan,2004.
