零行列式策略在雪堆博弈中的演化∗
2018-01-11王俊芳郭进利刘瀚沈爱忠
王俊芳 郭进利 刘瀚 沈爱忠
1)(上海理工大学管理学院,上海 200093)
2)(华北水利水电大学数学与统计学院,郑州 450046)
3)(西京学院商贸技术系,西安 710123)
零行列式策略在雪堆博弈中的演化∗
王俊芳1)2)郭进利1)†刘瀚3)沈爱忠1)
1)(上海理工大学管理学院,上海 200093)
2)(华北水利水电大学数学与统计学院,郑州 450046)
3)(西京学院商贸技术系,西安 710123)
零行列式策略,雪堆博弈,稳态分布,瞬态收益
1 引 言
博弈论是数学的一个分支,它是研究具有竞争与合作现象的理论和方法.20世纪50年代美国数学家Nash[1,2]提出了著名的纳什均衡,他指出当个体理性与集体理性冲突时,个体追求利己行为而导致的最终结局是一个“纳什均衡”.在纳什的影响下,Smith和Price[3]提出了演化博弈,旨在研究具有学习能力的有限理性个体以个人利益最大化为目标的群体博弈的演化稳定策略和演化均衡[4,5]的动态过程.大量的学者研究网络结构对合作行为的影响,提出异质网络结构有助于合作的产生[6−12],并从策略角度提出具有记忆的WSLS(win stay,lost shift),TFT(tit-for-tat)、GTFT(generous tit-for-tat)、无记忆的全合作策略和全背叛策略,讨论它们在重复博弈中的演化稳定性[13−15]及它们促使合作[16]的演化行为.在众多的策略中,没有一个策略可以单方面决定对手收益.Press和Dyson[17]于 2012年首次提出的零行列式策略(zero-determinant strategy)不仅可以单方面设计对手的收益,还可以采取适当的策略保证自己的收益为对方收益的倍数,从而达到敲诈的目的,所以也称敲诈策略.其优势受到了众多学者的广泛关注,人们在重复囚徒困境模型中集中研究零行列式策略的鲁棒性[18]及零行列式策略与WSLS、全合作策略、全背叛策略、TFT策略在群体博弈中的演化稳定性[19−23],并赋予节点不同的特性[23]讨论其对演化的影响及如何改变参数促使合作涌现.为提高其演化稳定性,文献[24—26]对零行列式策略提出了慷慨策略等其他子策略.零行列式策略的优势也被扩展至多人[27]及连续策略[28]情形;文献[29,30]将它们应用到公共物品博弈、重复噪音博弈等领域.
上述一阶记忆策略的收益都是基于遍历的Markov链的稳态分布计算的,在实际生活中,博弈双方可能更新策略很快,它们之间的转移矩阵也随之更换很快,导致稳态分布不易通过几次博弈即可达成.收益的计算在博弈中是非常重要的,收益的高低决定策略是否被选择,那么如果前期收益与稳态收益有差别,双方的期望收益能否直接用稳态期望收益替代?虽然Press和Dyson[17]指出对手不可能通过反复变换策略,使得稳态分布不能达到,从而破坏敲诈策略所设置的两者收益的线性关系.但是其前提条件是博弈次数足够大,也就是忽略前有限次博弈的影响,从而双方收益的线性关系是建立在长时期内平均收益之间的关系,但实际生活中,如果博弈次数不是足够多,讨论博弈前期的收益还是有必要的.另外进化人与零行列式策略博弈的进化结果都是基于仿真,并没有理论的支撑.
本文首先论证进化人与敲诈策略博弈时的部分进化结果,通过仿真比较各种情况下的进化速度并分析演化结果;着眼于博弈前期与稳态期,给出雪堆博弈中敲诈策略与全合作策略的瞬态分布、瞬态收益及相对盈余;其次讨论两时期双方收益的关系,实际敲诈因子的变化趋势;最后讨论敲诈因子对稳态分布和达到稳态所需博弈次数的影响.
2 雪堆博弈中的敲诈策略
雪堆模型中,A,B双方采取合作C与背叛D的支付矩阵如表1所列.

表1 雪堆博弈双方的支付矩阵Table 1.Payo ffmatrix in snowdrift games.
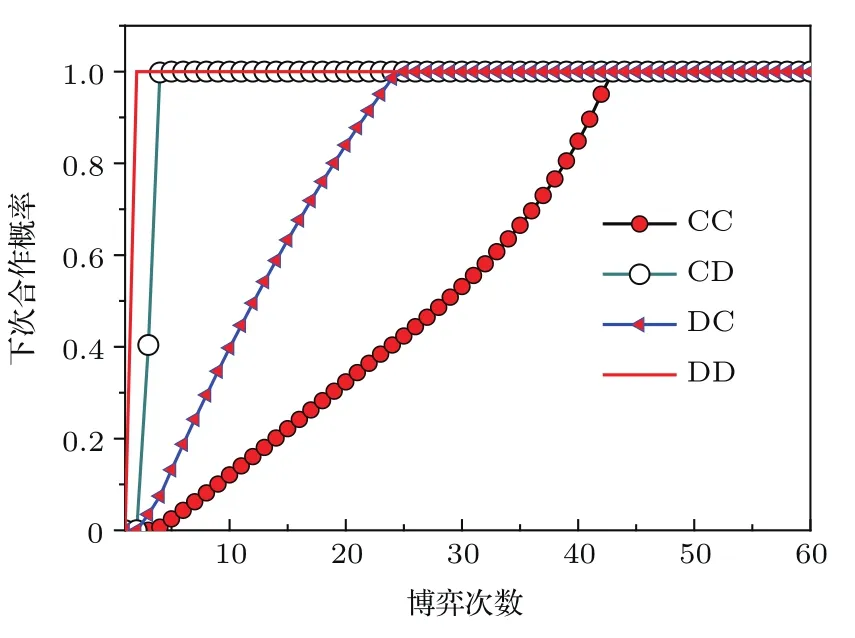
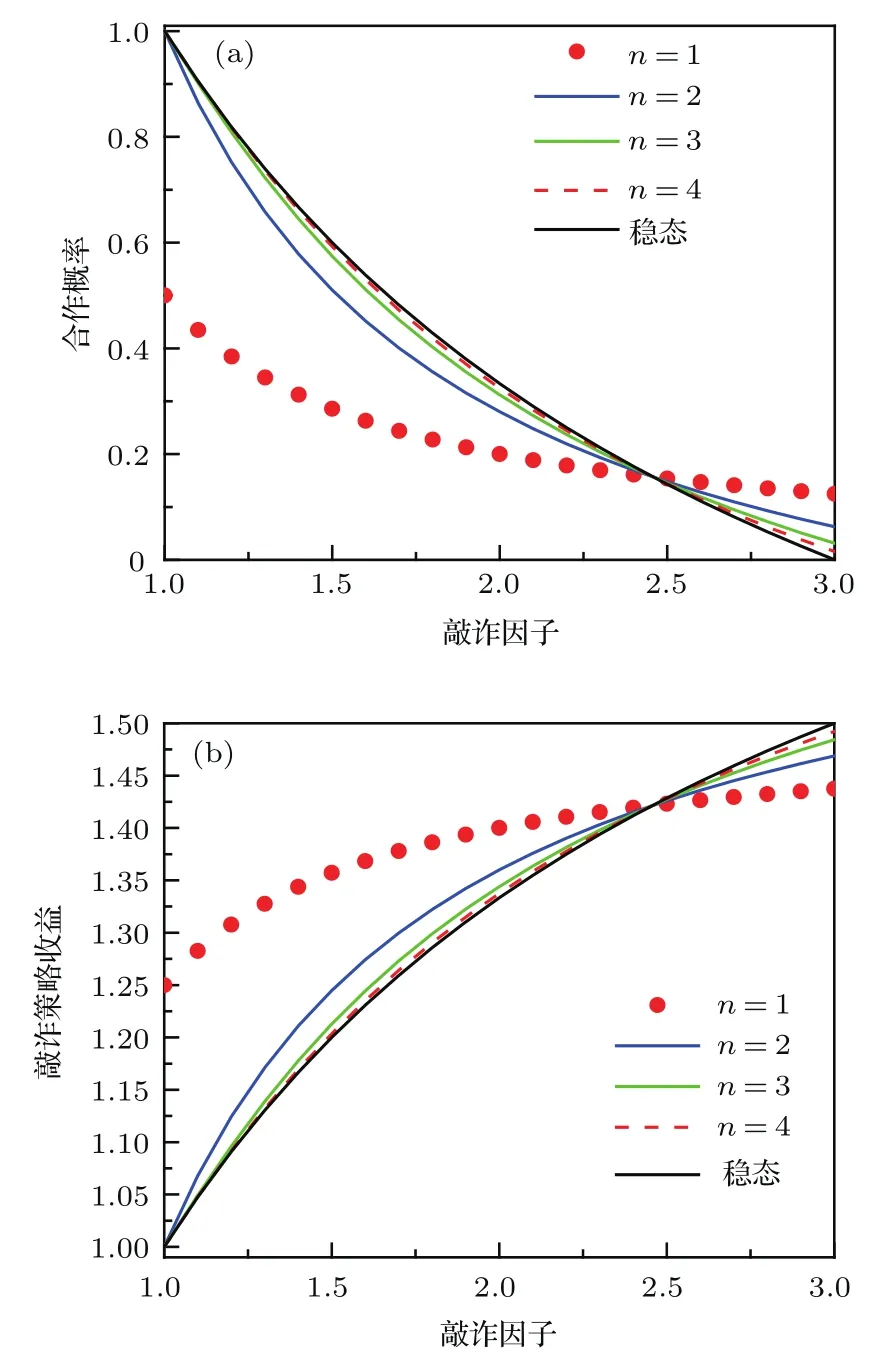
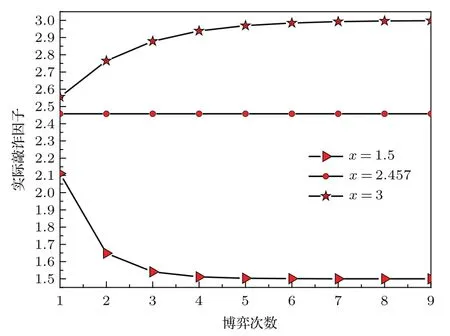
表1中0 双方下轮采取合作的概率分别为 则状态转移矩阵为 其平稳分布为v,由于矩阵P有单位特征根,令M=P−I,则|M|=0,其伴随阵为M∗,若rank(M)=3,则rank(M∗)=1,且 这里rank(M)代表矩阵M的秩,则M∗的每一行均与vT成比例.不妨设最后一行为N,由平稳分布的定义得 设M矩阵的最后一列为m,则 所以 其中 将矩阵的最后一列替换为向量SA−xSB,则A,B的稳态期望收益的线性函数为 即A的收益为B的收益的x倍,当x>1时,A达到敲诈B的目的,称x为敲诈因子. 一般情况下,敲诈策略与对手B博弈时,B的收益 记行列式D(p,q,SB)为D1,其余子式为Mij,D(p,q,1)的余子式为则 由于矩阵M与D1的第四列的代数余子式相同,且M的第四列的代数余子式均与平稳分布vT成比例,所以D1的第四列的代数余子式与vT成比例,由于vT的各元素为概率,所以同号,也即D1的第四列的代数余子式同号,所以M44与M14异号. 所以 作为理性的进化人B,刚开始博弈时,并不知道采取什么策略会使得自己的收益最大,设初始策略为全背叛策略,不断调整自己的策略q=(q1,q2,q3,q4)使自己的收益得到提高,调整的(原则是根据其收益)sB关于四个变元的梯度的正(负)方向增加(减少)合作的概率.由(12)式知,进化人B在双方背叛的情况下,会持续增加合作概率,最终调整为合作策略,对于其他三种情况下合作概率的调整可参见仿真图1.设定参与人B调整的幅度与该状态下的梯度大小成正比.比较四条曲线变化的快慢可知,如果进化人初始时刻采取全背叛策略,进化人在其背叛状态下,下轮马上转化为合作,其次为敲诈者背叛而进化人合作,进化速度最慢的为双方均合作情形,最终四种情形下均进化为合作策略.上述结论是基于进化人对零行列式策略不知情,追求自身收益最大化的进化结果;一旦进化人掌握了零行列式策略,他可能为了收益继续保持合作,也可能效仿对手,也采取零行列式策略,这时双方就会转化为谈判阶段,这里不再展开讨论. 图1 (网刊彩色)进化人在四种状态下的合作概率曲线Fig.1.(color online)Cooperation probability curves of evolutionary in the four states. 其中P为满足(6)式的敲诈策略.由图1可知,进化人根据梯度的方向调整合作的概率确实能找到使得自身的收益达到最大的策略——全合作策略,敲诈者A和全合作者B的稳定的平均收益为 仿真结果表明敲诈策略能促使对方合作,但自身并不会完全合作,这样的策略组合是否为纳什均衡呢? 则敲诈策略为 记 由于 苗木作为人工造林的基础,其质量对人工造林的成功起着关键作用。选择中年树木作为母树,可以充分利用其丰富的营养和较短的果期,保证苗木质量。在苗期,由于其根系较弱,但生长速率较低。快,所以需要很多水。同时,幼苗对生长环境也有一定的要求。因此,在育苗时,有关人员应做好监督管理工作,充分保证苗木的水肥供应。造林用苗木具有不同的成分,不同苗木的生存和生长。因此,针对不同的苗木,应采取不同的栽培技术,以保证苗木的存活。 其中X∗为全背叛策略,很明显(P∗,Y∗)不是该博弈的纳什均衡,所以敲诈策略只是一个促使合作的催化剂,但若A坚持敲诈策略,该演化结果可以持续下去. 以上所谈的双方收益都是基于n阶状态转移矩阵达到稳定状态下讨论的,但是从博弈的初始状态至稳态是需要时间的,即需要经过数次博弈才能使得CC,CD,DC,DD四种状态的概率趋于稳定,然而实际生活中,人是会不断学习的,如果策略更新很快,博弈者之间的转移矩阵也不断更换,很难在几次博弈下就达到稳态,而博弈前期的收益与稳态下的收益是有出入的.下面着眼于博弈前期,讨论博弈状态的瞬态分布与瞬态收益,其更接近生活中的博弈收益,并探求接近稳态需要的博弈次数n与敲诈因子的关系,为传统收益的应用提供一个借鉴条件. 敲诈者与全合作者初次博弈时没有上次的博弈信息可以参考,不妨设第0次博弈的四种状态各占0.25,由全概率公式,初始博弈敲诈者合作的概率 由于对方必合作,所以第一次博弈双方状态的分布 则敲诈者与全合作者的状态转移矩阵为 该一阶转移矩阵的元素均为正,则该Markov链为遍历的,n步转移矩阵 给定一个初始状态,经过n次博弈,其状态分布满足得 稳定状态的分布 结合(14)和(15)式,第n次博弈时双方受益表示为 由于敲诈因子反映了稳态时期敲诈策略与全合作策略的相对盈余,博弈初期的收益与稳态期不同,记实际敲诈因子xn为第n次博弈时敲诈策略与全合作策略的相对盈余,则 图2 (网刊彩色)(a)前四期与稳态情况下双方合作的概率曲线;(b)前四期与稳态情况下敲诈策略的收益曲线Fig.2.(a)The probability curves of cooperation in the previous four states and steady state;(b)the payo ffcurves of zero-determinant strategy in the previous four states and steady state. 由(14)和(15)式知,双方收益与敲诈者实施的策略(p1,p2,p3,p4)中的参数φ及r无关,但稳定状态vCC关于敲诈因子单调递减,敲诈因子越大,B的收益越低,A的收益越高.这是因为,在大的敲诈因子下,敲诈方在明知对方一定合作的情形下,一定会减少合作的概率,而坐享收益,敲诈方就是通过合适的策略使得对方必须合作,再经常背叛善良的合作方,而达到远远高于对方的收益. 现实生活中,大的生产商经常采取敲诈策略与小的零件供货商博弈,小的零件商为追求自身利益不得不和生产商合作,生产商不应该一味追求高的利润而一味敲诈对方,当被敲诈因子过大时,全合作者利润过小,达到底线时,就会采取背叛或放弃与大公司的博弈,而选择其他对手,这样都会使得敲诈者的收益受损,所以当对方完全合作时,应该适当降低敲诈,激励对方,从而达到共赢的目的. 名义敲诈因子x是敲诈策略拥有者想从合作者处获得巨额利润的预期值.由图3知,给定r=0.5时,当名义敲诈因子小于2.457时,博弈初期,敲诈者与合作者盈余比(实际敲诈因子)是高于敲诈者的预期的,经过几次博弈后,逐渐递减至预期值;当名义敲诈因子高于2.457时,初期的盈余比低于预期盈余比,并逐渐增加至预期值;当等于2.457时,整个博弈期不变. 图3 (网刊彩色)实际敲诈因子的变化曲线Fig.3.(color online)The curves of real extortion factor. 前面讨论了博弈初期的状态与博弈次数及敲诈因子的关系,稳态分布是一个极限分布,所以考虑博弈结果无限接近稳态只需要误差足够小即可,下面讨论在一定误差范围内,接近稳态所需博弈次数与敲诈因子的关系. 定理敲诈策略与全合作策略博弈达到稳态分布所需博弈次数与敲诈因子成正比. 证明设当Qn−Q∗的每个元素的绝对值均小于足够小的ε时,则状态趋于稳定, 总之,敲诈因子越大,达到稳定状态所需的博弈次数越多.接近稳态所需博弈次数与敲诈因子的关系如图4(b)所示. 图4 (网刊彩色)(a)状态转移矩阵与其极限的偏差曲线图;(b)接近稳态所需博弈次数(ε=1×10−5=0.5)Fig.4.(a)The curves of deviation between transfer matrix and it’s limitation;(b)game times to steady state(ε=1×10−5=0.5). 目前我国秋冬季节环境污染越来越严重,特别是北方地区,环境治理刻不容缓,但是环境治理的成效又受到周边环境的影响,目前以地方政府为主体的经济竞争模式导致地方政府放松对环境监管及治理的行为.因此地方政府对环境治理的态度直接影响着自身与周边地区的利益,地方政府间的博弈矩阵见表2. 表2 地方政府间污染治理支付矩阵Table 2.Payo ff s of two local governments in pollution management. 该博弈中,如果地方政府1治理,地方政府2的最佳策略为不治理,如果地方政府1不治理,则地方政府2的最佳策略为治理.如果地方政府2更追求经济效益,而经常搭便车,会使得地方政府1不得不必须采取治理策略以保证更大的经济与生态的加权收益.在重复博弈中,基于这样的两主体,地方政府1非常被动,如果政府1采取零行列式策略是可以改变这种困境的.不妨设敲诈因子x=2,=0.3,在上轮双方为(治理,治理),(治理,不治理),(不治理,治理),(不治理,不治理)时,政府1下轮采取治理的概率分别为 即可.如果政府2分别采取总不治理(All D)、等概率随机选择治理(Random)、总治理(All C)的策略,双方的稳态收益及政府2采取总治理策略时双方的即时收益见表3. 表3 政府1与政府2的即时收益与稳态收益Table 3.The transient incomes of two local governments. 由表3知,在地方政府1的零行列式策略下,地方政府2的最佳策略为全合作,即总是治理污染.因此政府1有效地发挥了政府2的主观能动性,保证污染总是被治理,同时自身也是以很大概率承担治理污染的责任,改变了政府2总是搭便车的格局.其次,该策略相对于TFT策略惩罚对手要温和一些,TFT对手的一次背叛引发其永久背叛,而零行列式策略遭遇对手背叛时仍能以一定概率合作,这就使得合作局面容易形成;并且实施零行列式策略者可以保证收益总是高于对手,如果设定的敲诈因子不是太大的话,前期他的收益要高于并逐渐逼近于稳定状态的收益. 1)在雪堆博弈中,论证了进化人与零行列式策略博弈时,如果进化人采取背叛策略,下轮博弈会很快进化为合作策略,并最终进化为全合作策略.结果表明零行列式策略是促使合作的手段,但并非一个均衡的结果. 2)当敲诈因子较小时,敲诈者的收益是逐次降低趋近稳态收益,敲诈者与全合作者相对盈余是高于并逐渐收敛到稳定状态的相对盈余,敲诈因子过大时,情况截然相反. 3)无论是博弈初期还是稳态期,高的敲诈因子都不利于敲诈者与全合作者双方相互合作. [1]Nash J F 1950PNAS36 48 [2]Nash J F 1951Ann.Math.54 286 [3]Smith J M,Price G R 1973Nature246 15 [4]Nowak M,Sigmund K 1990Acta Appl.Math.20 247 [5]Rodriguez I N,Neves A G M 2016J.Math.Biol.73 1665 [6]Xiang H T,Liang S D 2015Acta Phys.Sin.64 018902(in Chinese)[向海涛,梁世东 2015物理学报 64 018902] [7]Szabó G,Fáth G 2007Phys.Rep.446 97 [8]Zhang J J,Ning H Y,Yin Z Y,Sun S W,Wang L,Sun J Q,Xia C Y 2012Front.Phys.7 366 [9]Wu Y H,Li X,Zhang Z Z,Rong Z H 2013Chaos Soliton.Fract.56 91 [10]Yang H X,Wang B H 2012J.Univ.Shanghai Sci.Technol.34 166(in Chinese)[杨涵新,汪秉宏 2012上海理工大学学报34 166] [11]Xu B,Li M,Deng R P 2015Physica A424 168 [12]Newth D,Cornforth D 2008Artif.Life Robot.12 329 [13]Nowak M 1990Theor.Popul.Biol.38 93 [14]Lorberbaum J 1994J.Theor.Biol.168 117 [15]Imhof L A,Fudenberg D,Nowak M A 2007J.Theor.Biol.247 574 [16]Yi S D,Baek S K,Choi J K 2017J.Theor.Biol.412 1 [17]Press W H,Dyson F J 2012PNAS109 10409 [18]Chen J,Zinger A 2014J.Theor.Biol.357 46 [19]Adami C,Hintze A 2013Nat.Commun.4 2193 [20]Stewart A J,Plotkin J B 2013PNAS110 15348 [21]Hao D,Rong Z H,Zhou T 2014Chin.Phys.B23 078905 [22]Szolnoki A,Perc M 2014Phys.Rev.E89 022804 [23]Xu B,Lan Y N 2016Chaos Soliton.Fract.87 276 [24]Rong Z H,Zhao Q,Wu Z X,Zhou T,Chi K T 2016Eur.Phys.J.B89 166 [25]Li Y,Xu C,Liu J,Hui M P 2016Int.J.Mod.Phys.C27 306 [26]Liu J,Li Y,Xu C,Hui P M 2015Physica A430 81 [27]Hilbe C,Wu B,Traulsen A,Nowak M A 2014PNAS111 16425 [28]Mcavoy A,Hauert C 2016PNAS113 3573 [29]Pan L M,Hao D,Rong Z H,Zhou T 2015Sci.Rep.5 13096 [30]Hao D,Rong Z H,Zhou T 2015Phys.Rev.E91 052803 Evolution of zero-determinant strategy in iterated snowdrift game∗ Wang Jun-Fang1)2)Guo Jin-Li1)†Liu Han3)Shen Ai-Zhong1) 1)(Business School,University of Shanghai Science and Technology,Shanghai 200093,China) 17 March 2017;revised manuscript 30 May 2017) Zero-determinant strategy can set unilaterally or enforce a linear relationship on opponent’s income,thereby achieving the purpose of blackmailing the opponent.So one can extort an unfair share from the opponent.Researchers often pay attention to the steady state and use the scores of the steady state in previous work.However,if the player changes his strategy frequently in daily game,the steady state cannot attain easily.It is necessary to attain the transient income if there is a difference in income between the previous state and the steady state.In addition,what will happen if evolutionary player encounters an extortioner?The evolutionary results cannot be proven,just using the simulations in previous work.Firstly,for the iterated game between extortioner and cooperator,we introduce the transient distribution,the transient income,and the arrival time to steady state by using the Markov chain theory.The results show that the extortioner’s payo ffin the previous state is higher than in the steady state when the extortion factor is small,and the results go into reverse when the extortion factor is large.Furthermore,the larger the extortion factor,the harder the cooperation will be.And the small extortion factor conduces to approaching the steady state earlier.The results provide a method to calculate the dynamic incomes of both sides and give us a time scale of reaching the steady state.Secondly,for the iterated game between extortioner and evolutionary player,we prove that the evolutionary player must evolve into a full cooperation strategy if he and his opponent are both defectors in the initial round.Then,supposing that the evolutionary speed is proportional to the gradient of his payo ff,we simulate the evolutionary paths.It can be found that the evolutionary speeds are greatly different in four initial states.In particular,the evolutionary player changes his strategy into cooperation rapidly if he defects in the initial round.He also gradually evolves into a cooperator if he cooperates in the initial round.That is to say,the evolutionary process relates to his initial behavior,but the result is irrelevant to his behavior.It can be concluded that the zero-determinant strategy acts as a catalyst in promoting cooperation.Finally,we prove that the set of zero-determinant strategy and fully cooperation is not a Nash equilibrium. zero-determinant strategy,snowdrift game,stationary distribution,transient income PACS:02.50.Le,87.23.Ge,89.75.Fb,02.50.GaDOI:10.7498/aps.66.180203 *Project supported by the National Natural Science Foundation of China(Grant No.71571119)and the Young Scientists Fund of the National Natural Science Foundation of China(Grant No.11501199). †Corresponding author.E-mail:phd5816@163.com (2017年3月17日收到;2017年5月30日收到修改稿) 零行列式策略不仅可以单方面设置对手收益,而且可以对双方的收益施加一个线性关系,从而达到敲诈对手的目的.本文针对零行列式策略博弈前期与稳态期的收益存在偏差,基于Markov链理论给出零行列式策略与全合作策略博弈的瞬态分布、瞬态收益及达到稳态所需时间.发现在小的敲诈因子下,敲诈者前期收益高于稳态期收益,敲诈因子较大时,情况截然相反,并且敲诈因子越大,越不利于双方合作,达到稳态也越慢.这为现实生活中频繁更新策略的博弈提供了一种计算实时收益的方法.此外针对敲诈策略与进化人的博弈,论证了双方均背叛状态下,进化人下次博弈时一定进化为全合作策略.通过对所有状态下策略更新过程仿真,发现进化人在四种情况下的进化速度有显著差异,并最终演化为全合作策略,表明零行列式策略是合作产生的催化剂. 10.7498/aps.66.180203 ∗国家自然科学基金(批准号:71571119)和国家自然科学基金青年科学基金(批准号:11501199)资助的课题. †通信作者.E-mail:phd5816@163.com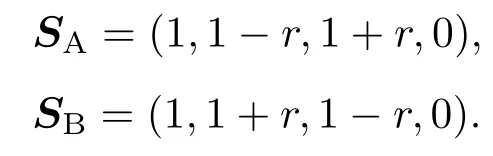
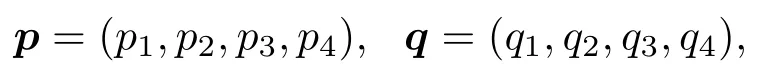
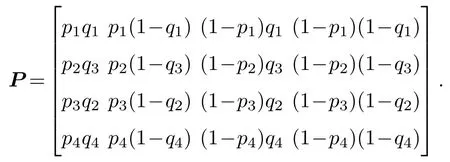

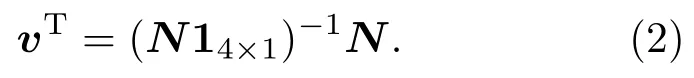
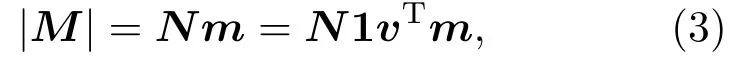
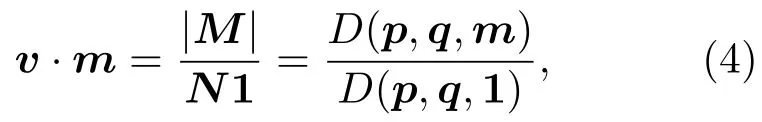
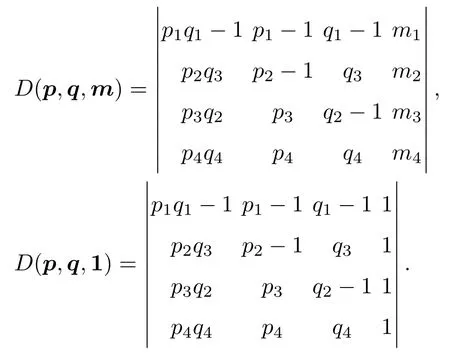
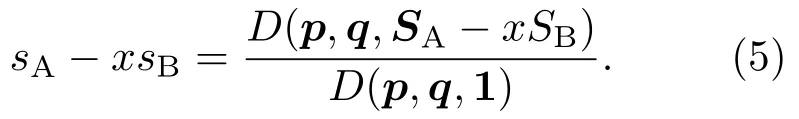
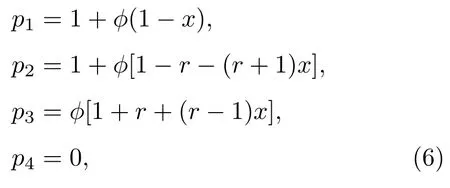

3 进化人在敲诈策略下的演化

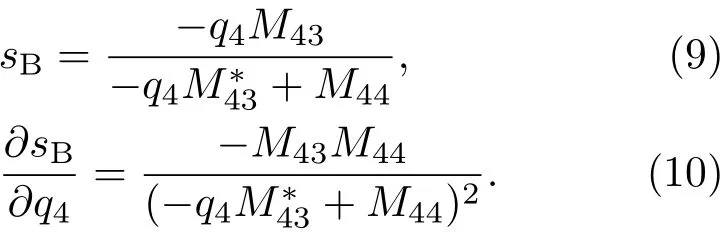
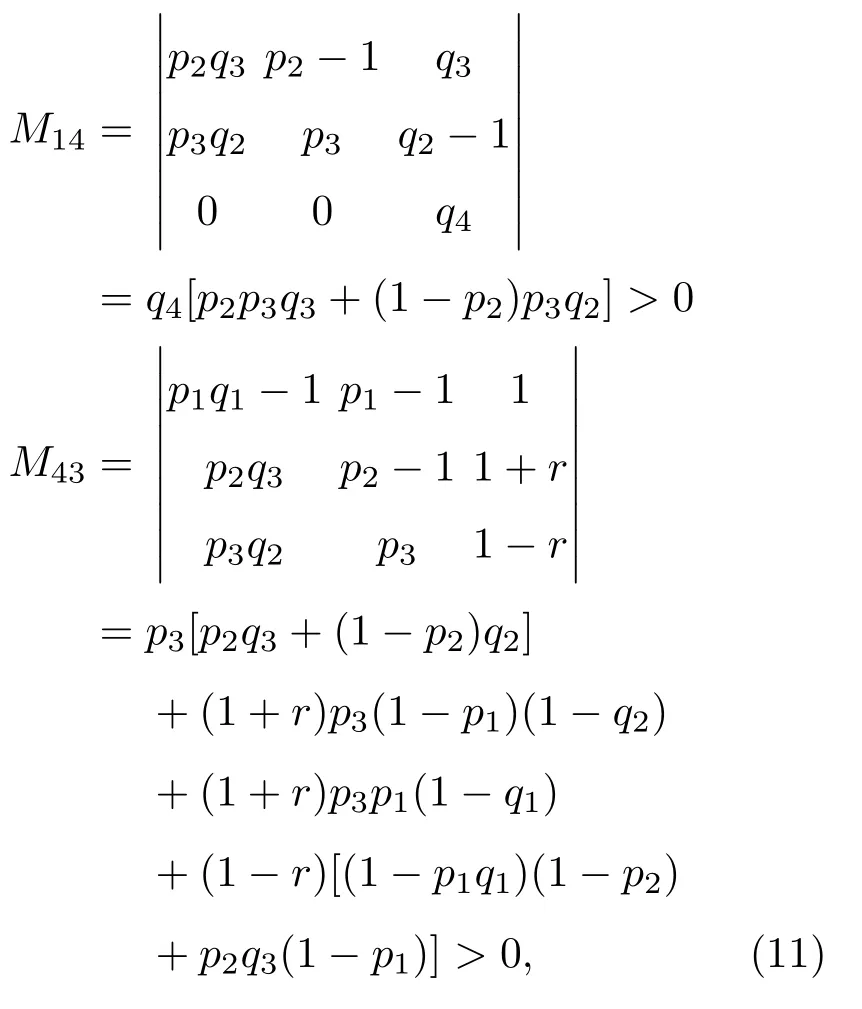

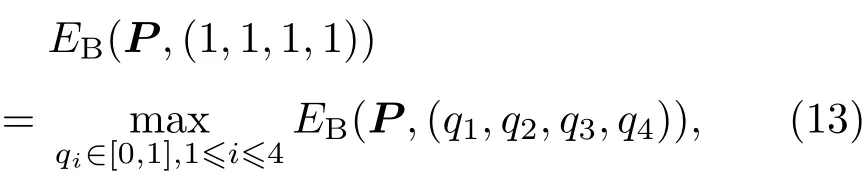
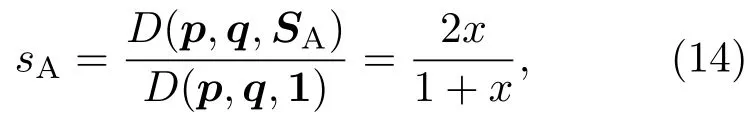
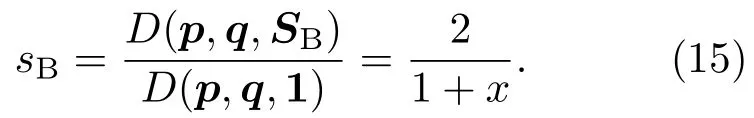

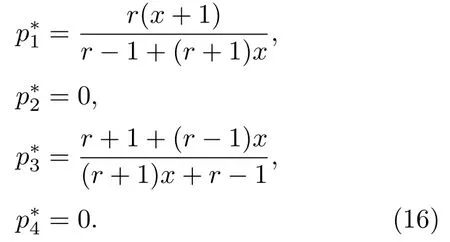
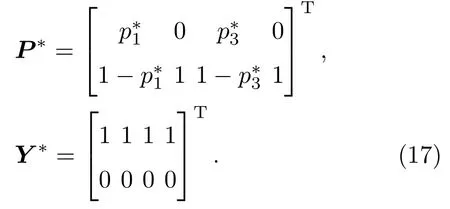
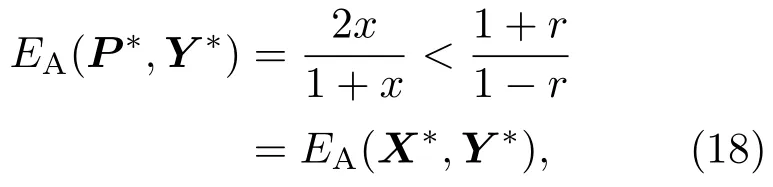
4 零行列式与全合作策略重复博弈的时变演化
4.1 敲诈策略与全合作策略博弈初期和稳态期的状态的瞬态分布及瞬态收益
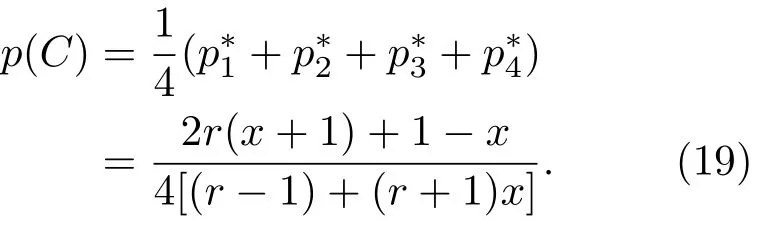
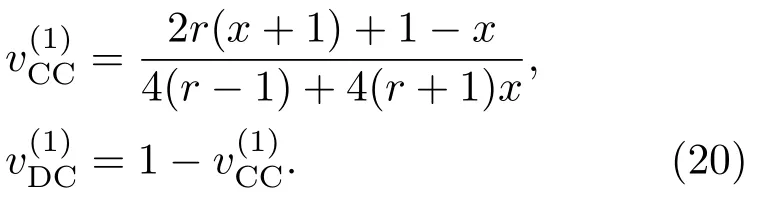
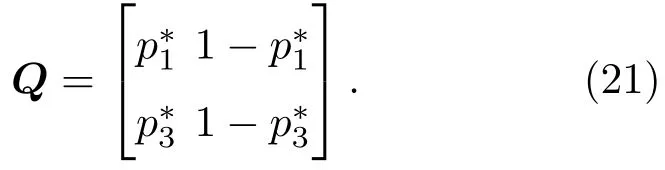
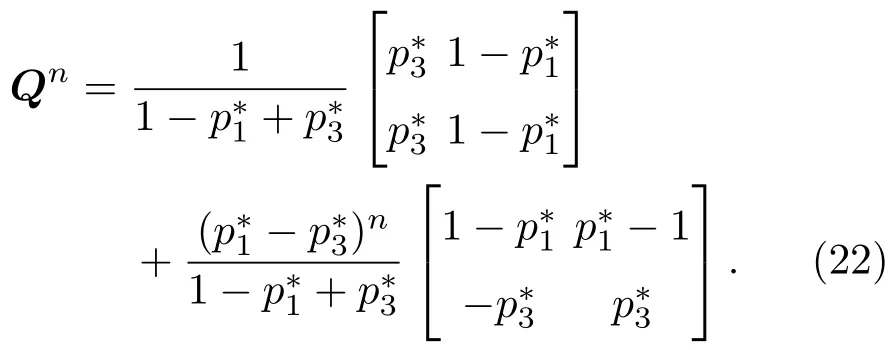
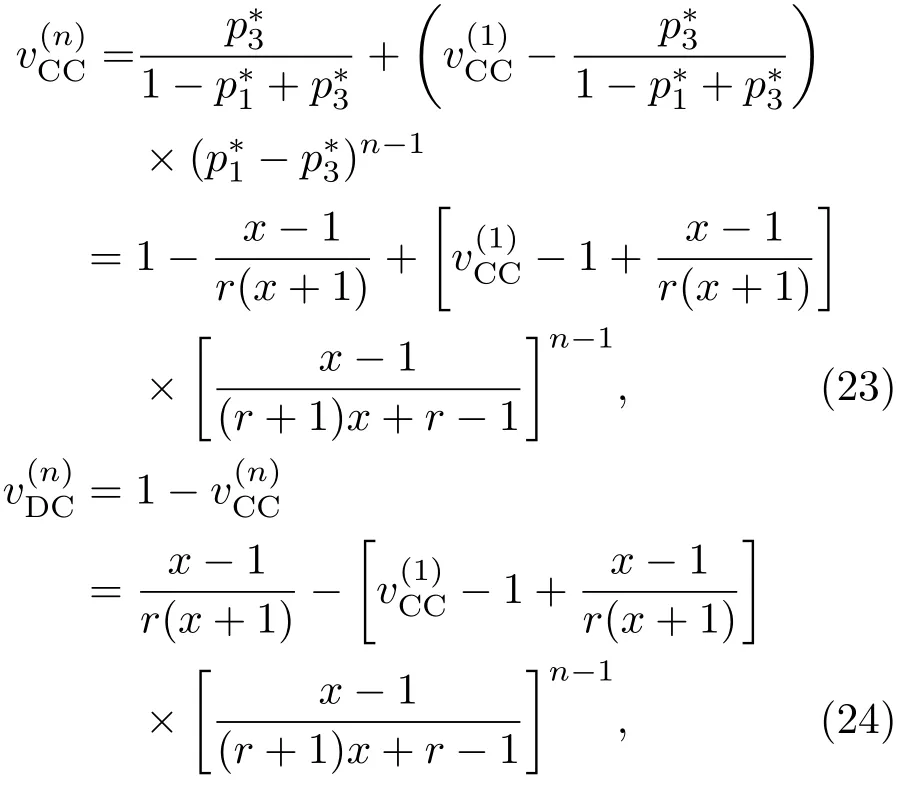
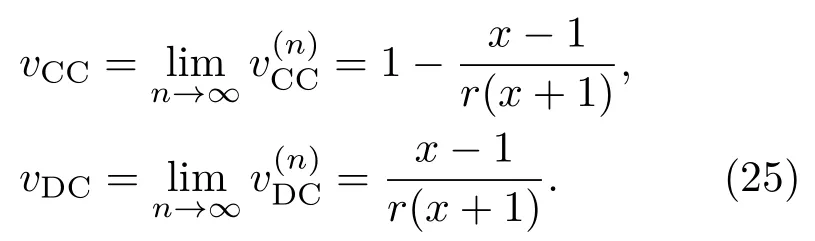
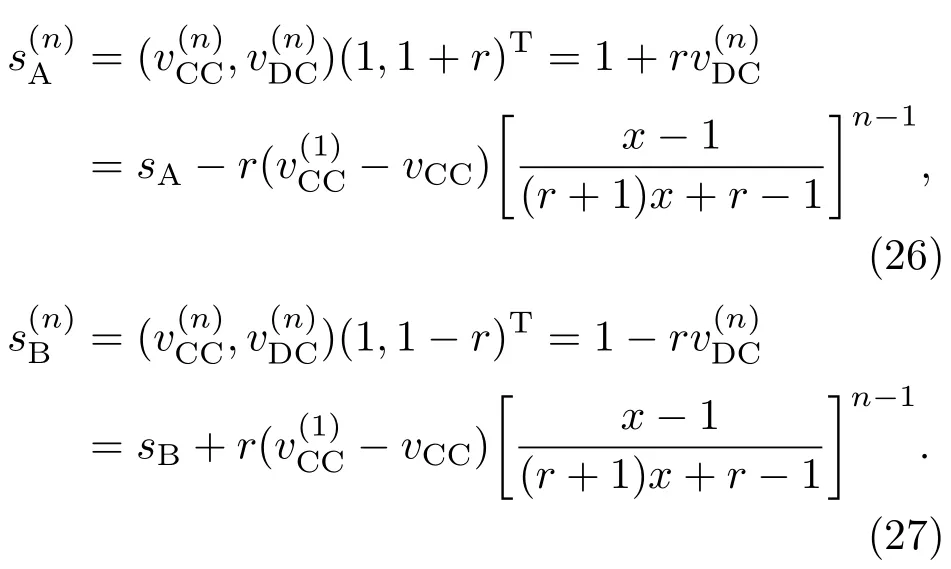
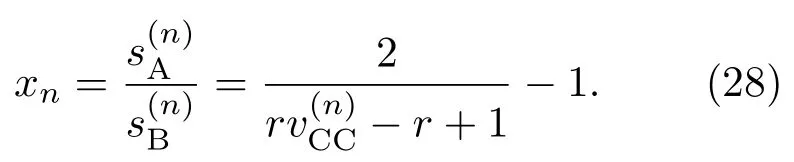
4.2 博弈的状态分布、收益与博弈次数及敲诈因子的关系
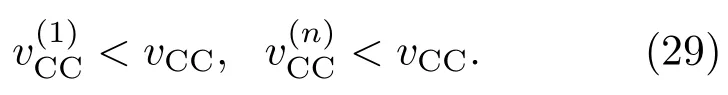
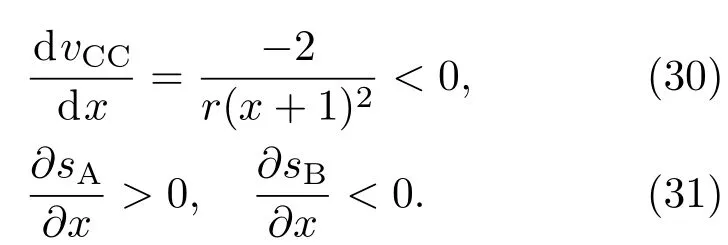
4.3 趋于稳定状态所需博弈次数与敲诈因子的关系
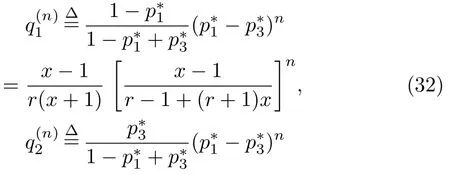
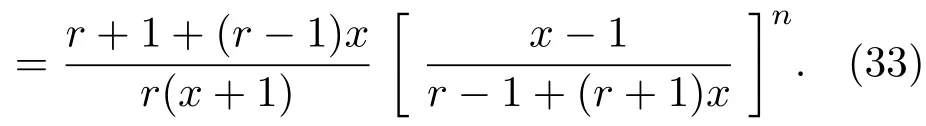
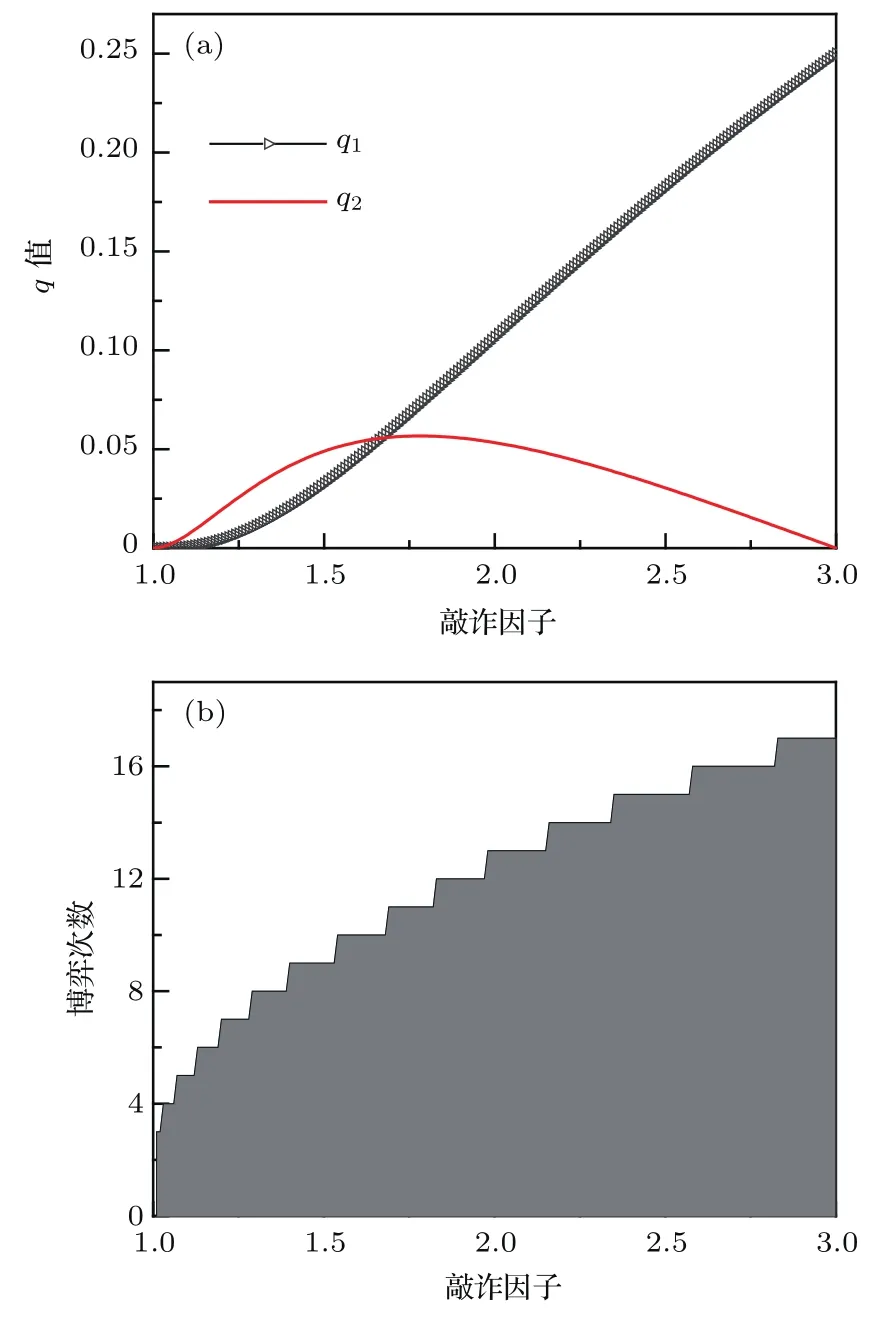
5 实例研究

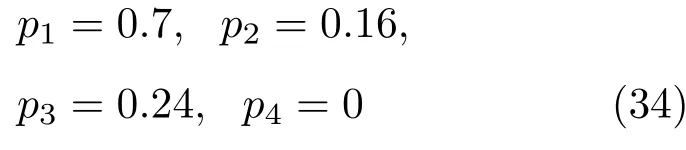
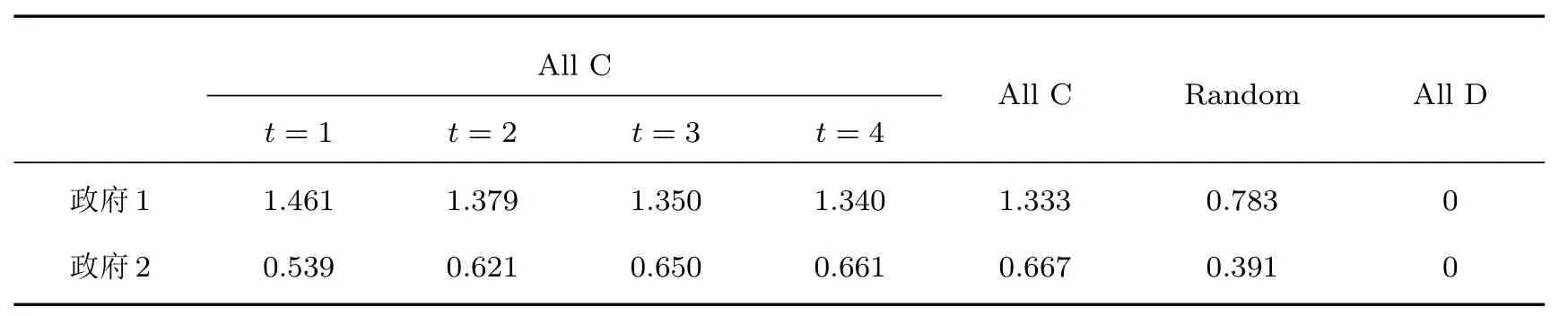
6 结 论
2)(School of Mathematics and Statistics,North China University of Water Resources and Electric Power,Zhengzhou 450046,China)
3)(Trade and Technology Department,Xijing University,Xi’an 710123,China)
