广东省佛山市第一中学(528000) 吴统胜

清华大学自动化系(100084) 李家昊(学生)

题海无涯,感悟是岸!—由一道高考压轴题谈函数型不等式解法的优化、推广与再应用

广东省佛山市第一中学(528000) 吴统胜

清华大学自动化系(100084) 李家昊(学生)

笔者在贵刊2017年第6期(上半月)刊出的“例谈妙用函数型不等式巧解导数压轴题”一文,在文末方法优化再拓展中提及了将y=ex,y=lnx(x＞0),y=xlnx(x＞0)放缩为一次函数形式的三个放缩的“一般式”,但因篇幅所限,当时未展开举例说明其应用.现本文将从一道函数型不等式高考压轴题的不同解法出发,对解法进行了较深入的探究、优化、拓展推广、原创了该类函数型不等式压轴题的一般化、“套路化”的解法,并对该原创解法进行了举例应用.

一、问题提出

例1(2013年课标II理科21题)已知函数f(x)=ex-ln(x+m).(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;(2)当m≤2时,证明：f(x)＞0.

解析 (1)略;(2)当m≤2时,f(x)=ex-ln(x+m)≥ex-ln(x+2).

证法一(构造函数法)构造函数φ(x)=ex-ln(x+2),转化为求φ(x)min=φ(x0)＞0.

设φ(x)=ex-ln(x+2),则在 (-2,+∞)上单调递增.又φ′(-1)＜0,φ′(0)＞0,所以φ(x)=0在(-2,+∞)上有唯一实根,且x0∈(-1,0).

当x∈(-2,x0)时,φ′(x)＜0;当x∈(x0,+∞)时,φ′(x)＞0,所以φ(x)min=φ(x0).由φ′(x0)=0得

证法二 (利用“公切线”法,转化为证明ex≥kx+b≥ln(x+2).)设φ(x)=ex,h(x)=ln(x+2)的的公切线为y=kx+b(k/=0).设两切点分别为M(m,em),N(n,ln(n+2)),利用切线斜率相等得

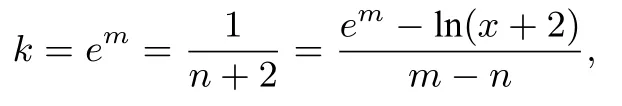
当n=-1时,所以M(0,1),N(-1,0),对应公切线为y=x+1.

(当n=e-2时,所以对应公切线为

我们不妨取公切线为y=x+1.利用构造函数法易证：

但两不等式不同时取等号,所以ex＞ln(x+2).所以当

证法三 利用常见函数型不等式ex≥1+x或ln(x+1)≤x,(x＞-1)(见人教版教材《选修2-2》P32题1.3B组第1题).

因为lnx≤x-1(x＞0),所以ln(x+2)≤x+1(x＞-2)当且仅当x=-1时取等号.又因为ex≥x+1当且仅当x=0时取等号.所以当m≤2时,f(x)=ex-ln(x+m)≥ex-ln(x+2)＞x+1-(x+1)=0.所以f(x)＞0.因为两等号不同时取,所以当m≤2时,f(x)＞0.

点评 证法一转化为求函数的最小值,思路虽简单,但由于最小值φ(x0)对应的x0不可求,需利用函数零点存在定理及设而不求法才可以较巧妙地解决证明问题,对思维及转化能力的要求相当高.证法二利用“公切线”法证明函数型不等式,可以化曲为直,方法相当精妙,也可实现对不等式的精准放缩,证明方向相当明确.此方法适用于一凸、一凹函数类型,若两函数同为凸函数或凹函数,则该方法不可用,但可对原不等式作适当变形,转化为不等式两边分别为一凸、一凹函数类型,再用“公切线”法证明,但求公切线的过程计算稍显麻烦!证法三利用常见函数型不等式证明,过程简单,但放缩的“度”不好把握,不一定恰好成功!

能不能找到更好、更简洁明了的方法,可以快速直接地把ex,lnx,xlnx放缩为以下类型ex≥kx+m,lnx≤kx+m,xlnx≤kx+m?答案是肯定的!

下面把证法二、三的方法优化、整合拓展一下,可得如下一般性的放缩公式.

二、方法的优化、拓展、一般化

常见的函数y=ex,y=lnx,y=xlnx(x＞0)我们均可以把它们放缩为如下一次函数形式：

函数型不等式1 ex≥kx+k-k lnk,(k＞0).

简析 设f(x)=ex-kx(k＞0),易得x0=lnk是f(x)的极小值点.

函数型不等式2 lnx≤kx-lnk-1(x＞0,k＞0).

函数型不等式3 xlnx≥kx-ek-1(x＞0,k∈R).

简析 设f(x)=xlnx-kx(x＞ 0,k∈R),易证, x0=ek-1是f(x)的极小值点.

三、优化解法的再应用

1.函数型不等式1的再应用

例1(2013年课标II理科21)已知函数f(x)=exln(x+m).(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;(2)当m≤2时,证明 f(x)＞0.

解析 (1)略;(2)当m≤2时,

即证ex≥ln(x+2).由函数型不等式1得,

即只需证：kx+k-k lnk≥ln(x+2).设φ(x)=ln(x+2)-[kx+k-k lnk],所以时φ′(x)＞0,φ(x)递增;当时φ′(x)＜0,φ(x)递减.所以所以不妨取k=1或利用ex≥x+1或者均可得证原不等式!以下证明过程同证法二、三.

点评 本放缩方法完美地克服了证法二、证法三中的不足之处,思路清晰明确,可操作性强,按部就班,考生容易掌握!在实际解题中,我们只需通过观察得到k,使k满足即可,可以说该解法是快速解决此类函数型不等式压轴题的通性通法!

2.函数型不等式2的再应用

例2 求证：ex＞2x+lnx(x＞0).

解析 由函数数型不等式2得,lnx≤kx-lnk-1(k＞0),所以 lnx+2x≤ (k+2)x-lnk-1,即证 ex≤ (k+2)x-lnk-1,设h(x)=ex-[(k+2)x-lnk-1],(x＞0,k＞0),h′(x)=ex-(k+2),当x＞ln(k+2)时h′(x)＞0, h(x)递增;当0＜x＜ln(k+2)时,h′(x)＜0,h(x)递减.所以h(x)min=h(ln(k+2))=(k+2)[1-ln(k+2)]+lnk+1,只需取即可使

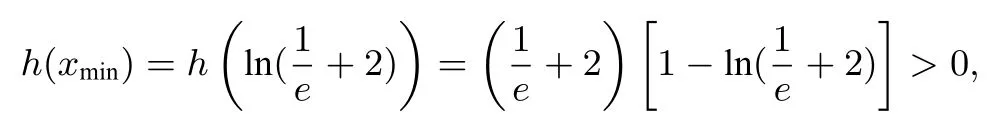
原不等式即可得证!

整理该证明过程如下：原不等式可转化为证明

易证 φ(x)max= φ(e)=0.再证明,设所以易证,所以φ(x)max＜g(x)min,所以ex＞2x+lnx,(x＞0).

点评 该解法是解决此类函数型不等式压轴题的通性通法!此题其实可利用常见函数型不等式进行放缩即可得证,若用lnx≤ x-1,(x＞ 0)进行放缩,则放得稍大了,证明不了!另外该题也可对要证不等式进行适当变形,转化为证明设(x＞0).易得：f(x)min=f(1)=所以f(x)min＞g(x)max,所以ex＞2x+lnx,(x＞0).即转化为两个函数的最大值、最小值的大小比较,利用构造函数的通法证明,证明过程相对较简便,但此类尝试往往不一定恰好成功!故要注意题型、方法的总结感悟,提升解决此类压轴题的能力!

3.函数型不等式3的再应用

例3求证：ex+ex-3＞1-x(1+lnx).(x＞0)

解析 原不等式即证,

由函数型不等式1得,ex≥kx+k-k lnk,(k＞0).

由函数型不等式3得,xlnx≥tx-et-1,(x＞0,t∈R).

由一次函数性质,要证

其中,易证k-klnk≤1当且仅当k=1取等号,不妨取k=1,即只需

点评 当证明思路不易找寻时,可采用该一般性的证明方法找寻解题思路,但可采用综合法书写证明过程.另外该题也可利用构造函数法直接证明,其证明过程如下：

所以f(x)＞g(x).所以原不等式得证!解题时要不断总结感悟解题思路和方法,提升解决此类函数导数不等式压轴题的解题能力!

常见函数型不等式如下：

图1

(见人教版教材《选修2-2》P32习题1.3B组第1题)

可结合图2加深学生对不等式的理解记忆.

图2

图3

(可结合下图3加深学生对不等式的理解记忆)

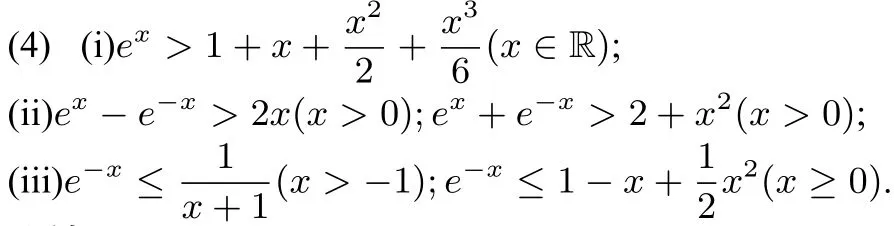
四、总结

函数型不等式压轴题的证明方法主要有构造函数法(有时需对要证不等式进行适当变形转化为两个函数的最大值与最小值大小比较,再利用构造函数法证明)、主元法、利用常见函数型不等式放缩法、利用放缩的“一般式”证明等方法,主要考查考生利用导数的工具研究函数的图像和性质,对思维要求高,综合性、方法性强,解题突破口不易找寻,需要考生在平时解题中不断总结、感悟题型和方法,尤其是解题思路的感悟反思,提升解决此类函数导数不等式压轴题的解题能力,正所谓“题海无涯,感悟是岸”!

五、反馈练习

1.(2017年佛山二模理科21)设函数f(x)=aex-xlnx,其中a∈R,e是自然对数的底数.(I)若函数f(x)是(0,+∞)上的增函数,求实数a的取值范围;(II)若证明f(x)＞0.

2.(2017年广州一模理科21)已知函数f(x)=lnx+(I)若函数f(x)有零点,求实数a的取值范围;(II)若时,证明

3.(2014年全国I理科第21题)设函数f(x)=aexlnx+曲线y=f(x)在点 (1,f(1))处的切线为y=e(x-1)+2.(I)求a,b;(II)证明f(x)＞1.

4.(2016广州一模理科题21题改编)求证：ex＞lnx+ 2(x＞0).

5.求证：ex≥x+lnx(x＞0).