福建省德化第一中学362500 吴志鹏

评析几种方案生成的离心率问题*

福建省德化第一中学362500 吴志鹏

离心率是圆锥曲线的一个重要元素,它的变化直接导致曲线形状甚至是类型的变化,求圆锥曲线的离心率或取值范围是近年高考的热点,这类问题所涉及的知识点较多、综合性强,解法灵活,极富内涵,这也是命题者亲睐的原因所在.对于这类问题的求解,学生怎样才能做到“以不变应万变”呢?本文从离心率问题的生成方法入手,帮助读者分析研究,以便寻找有效的方案解决之.

一、“代数方案”生成的离心率问题

这类问题利用了椭圆、双曲线方程标准形式中的参数,应用代数方案计算出有关参数的值或范围,进而获得离心率的值或范围.

例1(2008高考全国卷2理9)设a＞1,则双曲线的离心率e的取值范围是( )

图1

(I)求直线y=kx+1被椭圆截得的线段长(用a,k表示);

(II)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.

解 (I)设直线y=kx+1被椭圆截得的线段为AP,由得故因此

(II)假设圆与椭圆的公共点有4个,由对称性可设y轴左侧的椭圆上有两个不同的点P,Q,满足|AP|=|AQ|.记直线AP,AQ的斜率分别为k1,k2,且k1,k2＞0,k1/=k2.由(1)知：

由于k1,k2＞0,k1/=k2得

即转化为关于k1,k2方程有解的充要条件：1+a2(a2-2)＞1又因为a＞1,所以因此若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,由得离心率的取值范围

解 I由C与l相交于两个不同的点,故知方程组有两个不同的实数解,消去y并整理得

评析 以上三个例题均是通过代数方案生成的离心率问题.例1是通过对e的代数公式进行研究;例2是转化成方程有解求得离心率的范围;例3则是转化为判别式△＞0.

二、“几何方案”生成的离心率问题

利用几何性质获得e的值或范围,根据其考查目标的侧重点可分为以下三类：

1.以定义为抓手,利用性质建立的a,b,c齐次关系

图2

解 作图像如上图所示,依题意,不妨设AB=6,AD= 4,则

例5(2014重庆理8)设F1,F2分别为双曲线1(a＞0,b＞0)的左、右焦点,双曲线上存在一点P使得则该双曲线的离心率为( )

解 因为P是双曲线上一点,所以||PF1|-|PF2||=2a,又|PF1|+|PF2|=3b,所以(|PF1|+|PF2|)2-(|PF1|-|PF2|)2=9b2-4a2,所以4|PF1|·|PF2|=9b2-4a2,又因为所以有9ab=9b2-4a2,即解得故选B.

解 设左焦点为F1连接AF1,BF1,则四边形BF1AF是平行四边形,故|AF1|=|BF|,所以

所以a=2,设M(0,b),M到直线l的距离不小于得故b≥1,即a2-c2≥1,0＜c2≤3,所以选择A.

评析 以上三道例题均构造过焦点的三角形,只不过例4、例5的焦点三角形为显性,而例6却是隐性的,对于这种类型的问题则需先利用定义获得与参数a相关的等量关系,再通过寻找图形中的一些几何关系或利用题目所给的条件获得关于参数a,b,c的齐次关系,最后求得e的值或范围.

2.以点的坐标为抓手,利用性质建立的a,b,c齐次关系

例7(2016新课标III理11)设O为坐标原点,F是椭圆的左焦点,A,B分别为椭圆C的左、右顶点.P为C上一点,且PF⊥x轴.过点A的直线l与线段PF交于点M,与y轴交于点E,若直线BM经过OE的中点,则C的离心率为( )

解 设E(0,m),则直线因为F是椭圆的左焦点,PF⊥x轴,过点A的直线l与线段PF交于点M,联立两直线方程得是OE中点即由B,N,M三点共线可得：得a=3c,即

例8(2016年江苏理10)如图,在平面直角坐标系xoy中,F是椭圆的右焦点,直线与椭圆交于B,C两点,且∠BFC=90◦,则该椭圆的离心率是____.

评析 本题只需联立直线与椭圆的方程,求得点B,C的坐标,再利用BF⊥CF即即可求得a,c的齐次关系,答案为

例9(15年山东理科5)平面直角坐标系xOy中,双曲线的渐近线与抛物线C2:x2=2py(p＞0)交于点O,A,B,若△OAB的垂心为C2的焦点,则C1的离心率为___

又由于的C2:x2=2py(p＞0)焦点的垂心为C2的焦点,故有AF⊥OB,则即

例10(2014浙江理14)设直线x-3y+m=0(m/=0)与双曲线两条渐近线分别交于点A,B,若点P(m,0)满足|PA|=|PB|,则该双曲线的离心率是____.

评析 以上的四个例题均是以参数a,b,c相关点的坐标为抓手生成的问题,此类问题的设计不再局限于是否出现焦点三角形,它可以与圆锥曲线的的顶点、焦点、双曲线的渐近线、准线等与参数相关的量相结合,考查图像的几何性质,内容比较丰富.

3.利用特殊图形的几何性质,建立的a,b,c齐次关系

解 设M(c,0),N(0,b),在Rt△MON中,有

例 13(2012新课标高考 4)设F1,F2是椭圆E:的左、右焦点,P为直线上一点,△F2PF1是底角为30◦的等腰三角形,则E的离心率为( )

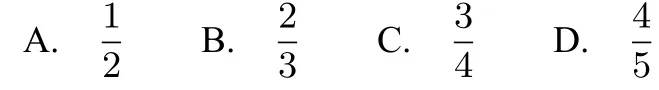
解 因为△F2PF1是底角为30◦的等腰三角形,得：

评析 以上几例均在圆锥曲线内构建直角三角形、等腰三角形、圆的切线、中位线等的特殊图形,通过考查这些图形的相关性质获得关于a,b,c的齐次关系,得椭圆E的离心率或范围.这类问题大多侧重于通过对图形的几何性质进行分析获得结论.

三、“三角方案”生成的离心率问题

在三角形内,以考查正弦定理、余弦定理为目标的离心率构造问题,此类问题经常结合圆锥曲线的定义与解三角形进行考查.

例14(2008全国卷1理15)在△ABC中,AB=若以A,B为焦点的椭圆经过点C,则椭圆的离心率e=___.

解 在△ABC中,可设AB=BC=t,利用余弦定理可知：AC2=AB2+BC2-2AB·BCcosB得为焦点的椭圆经过点C,依定义得|CA|+|CB|=2a,所以

变式 (2014大纲理9改编)已知双曲线C的焦点为F1,F2,点A在C上,若|F1A|=2|F2A|,且cos∠AF2F1=则双曲线C的离心率为___.

答案：2.

解 在△PF1F2中,由正弦定理可得

即c2-2ac-a2＜0,得e2-2e-1＜0.所以

又e＞1,所以

评析 以上两个例子及变式把圆锥曲线的离心率与解三角形完美的结合,通过正弦定理、余弦定理以及圆锥曲线的定义、几何性质,寻找出与参数a,b,c相关的齐次关系,得离心率的值或范围.

[1]杜红全.求离心率取值范围常用的方法与技巧[J].数学通讯(上半月),2015(5,6)

[2]武增明.探求圆锥曲线离心率的取值范围的思维途径[J].中国数学教育(高中版),2009(12)

[3]王勇.离心率—经久不衰的高考热点[J].数学通讯(上半月),2016(1, 2)

*本文系福建省教育科学“十三五”规划2016年度立项课题《高中数学生成性教学的理论认识与实践研究》成果.(立项批准号：FJJKXB16-330)