江苏省如皋市第二中学(226500)

王晓红●

韦达定理在圆锥曲线中的应用

江苏省如皋市第二中学(226500)

王晓红●

在圆锥曲线的求解过程中，我们常常需要设出很多的未知量，直线斜率、交点坐标、椭圆焦点等等.但我们一般不会详细求解出未知量，而是设而不求，从而简化计算过程.韦达定理以乘积、和的形式出现，正好体现了这类思想.在直线与椭圆、抛物线、双曲线等圆锥曲线的交点问题中，韦达定理发挥了重要的作用.本文将对韦达定理在圆锥曲线中的使用展开讨论.

一、在弦长求解方面的应用

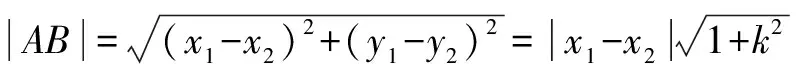
例1 已知直线2x+y+4=0和圆x2+y2+2x-4y+1=0，求过两者交点，且面积最小的圆的方程.

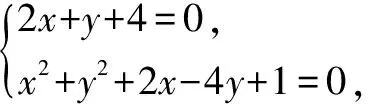
点评 本例属于对韦达定理在弦长求解中的直接应用，思路清晰，题眼明了.直接利用题目给出的已知条件，按照上述求解思想和步骤进行.

例2 如图所示，抛物线y2=4x的顶点是坐标原点，其中A点坐标为(5,0)，且线段OA与斜率为1的直线相交(O、A点非交点)，同时与抛物线有交点M、N，试求△MAN面积最大时的直线方程.

分析 欲求直线方程，首先设出直线方程为y=x+b，与抛物线联立后消去变量y，得到一元二次方程x2+(2b-4)x+b2=0.继续设出点M、N的坐标(x1,y1)、(y1,y2)，利用韦达定理便可以得到x1+x2与x1x2的值，代入弦长公式中，即可求出线段MN的长度.最后，结合点到直线距离，便可以表示出△MAN的面积公式，则可求出最值时的直线方程.

点评 韦达定理在弦长求解时，往往不会像例1那样直接考查.而是像例2一样，将弦长的应用蕴含在三角形面积、圆面积等其他考点中.但究其核心，其本质依然是“直曲联立求韦达”，采用设而不求的思想，并结合平方和公式，利用弦长进行求解.

二、在弦中点方面的应用

例3 已知，PQ是抛物线y2=4x的动弦，过点(0,3)的直线l为动弦的中垂线，若设α为直线l的倾斜角，试问该倾角的取值范围.

分析 欲求倾角的取值范围，即是求解直线l的斜率，则设出直线l的方程为y=kx+3(k≠0)，顺势可以求得直线PQ的方程.此时，将直线PQ的方程与抛物线的方程联立，可以得到关系式y2+4ky-4kb=0.进一步设出P、Q两点的坐标，利用韦达定理可以得到PQ中点的坐标.将其回代到直线方程中，得到k、b关系式.结合一元二次方程Δ>0，便可以求出斜率k的取值范围，则倾角取值也可求得.

点评 弦中点问题是韦达定理使用较为显著的题型，其关键依然是“直曲联立求韦达”，通过设出直线方程，交点坐标，同样采用“设而不求”的思路，利用联立所得到一元二次方程求出横纵坐标之间的数量关系，最终实现顺利求解.

总之，韦达定理在圆锥曲线中有着灵活的使用，以上针对韦达定理在抛物线与直线相交形成的弦长及弦中点求解的应用展开了论述.简言之，其内核即是“直曲联立求韦达”，再利用弦长公式、弦中点表达式实现对应问题的求解.

G632

B

1008-0333(2017)07-0027-01